在3D重建领域，这幅图怎么理解

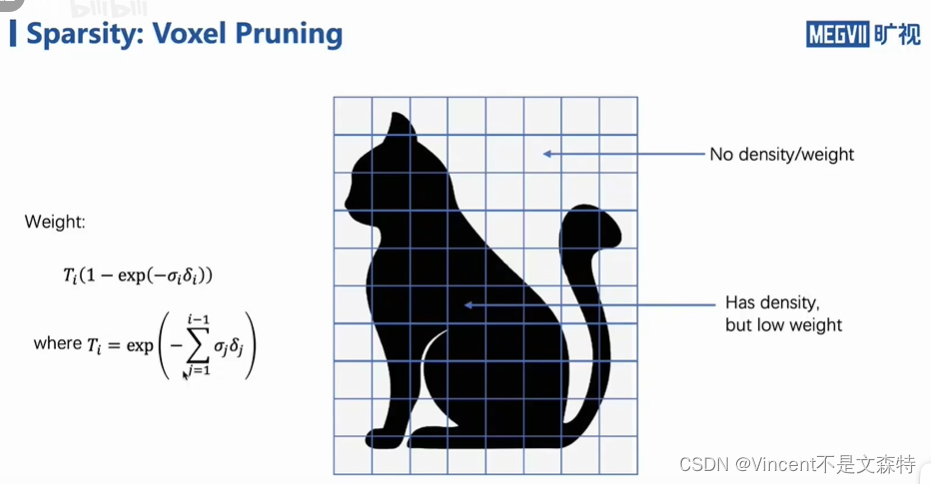
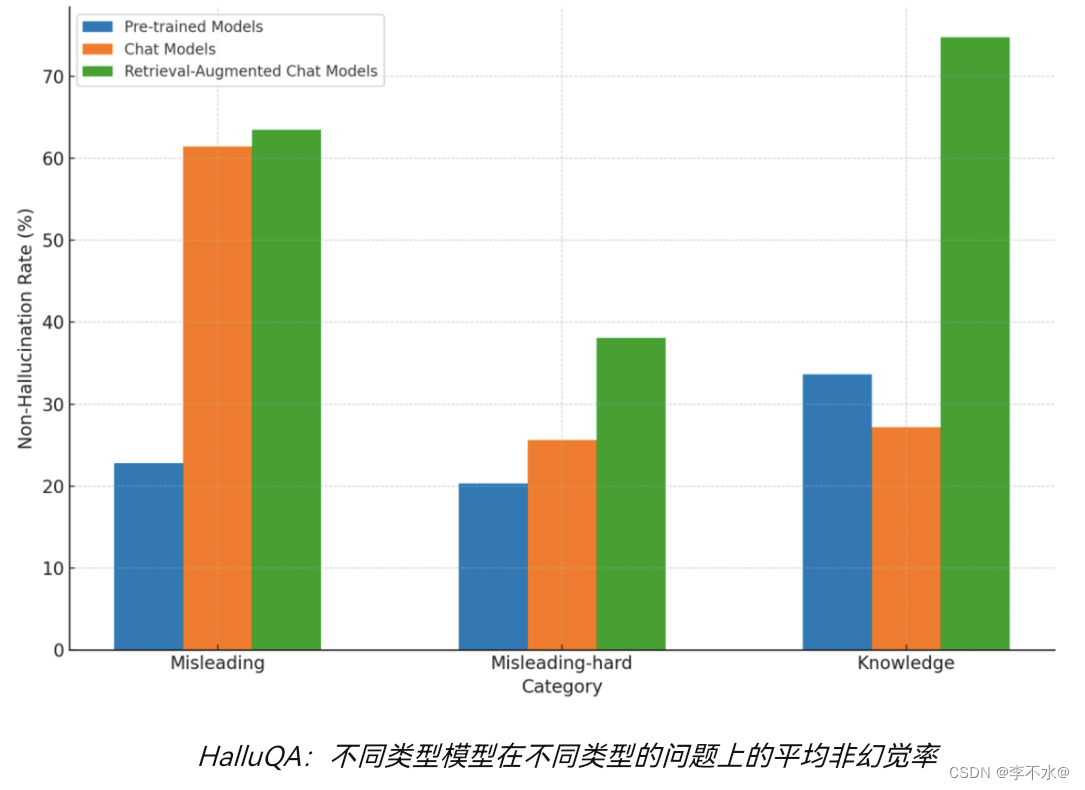
这张图展示的是“体素剪枝（Voxel Pruning）”在3D重建中的应用，这是一种利用稀疏性（Sparsity）来优化3D数据存储和处理的技术。体素剪枝的目的是为了降低存储需求和提高计算效率，通过去除那些不重要或权重较低的体素数据。

在图中，体素化的对象（如猫的轮廓）被映射到一个网格上，其中每个体素要么包含对象的一部分，要么是空的。以下是图中所示概念的详细解释：

• 有密度但低权重的体素：这些体素是对象的一部分，但它们的重要性或“权重”较低。在3D重建中，这可能意味着它们包含的信息对于描述整个形状不是特别重要，或者它们是由于噪声或其他因素而被错误地分类为对象的一部分。

• 无密度/权重的体素：这些体素不包含任何对象的部分，它们是完全空的。在3D重建中，这些体素不携带任何有关形状的信息，因此可以被移除以减少数据的体积。

图中还展示了一个公式，它描述了体素权重的计算方式。这个权重可能与体素包含对象的密度有关，或者与体素在重建过程中的重要性有关。这个公式具体如下：

$$T_i$$ 是一个递减的项，可能表示体素的重要性，随着从表面向内部的深度增加而减少。
$$\sigma$$ 可能是一个与体素密度相关的参数。
$${\delta }_i$$ 可能是与体素在某一维度（如深度）上的位置相关的参数。

体素剪枝通过移除那些权重低于某个阈值的体素来工作。这个过程可以显著减少在存储和处理3D数据时所需的资源，同时还能保持对整体形状的足够描述。

具体详细说说这个公式

这个公式是体素剪枝中用来计算体素权重的公式，其中涉及到两个主要的部分：$$体素的当前权重T_i和它的调整因子(1-\exp (-{\sigma }_i{\delta }_i))。$$让我们分解这个公式：

体素权重 $$T_i$$：

$$T_i$$ 代表第i个体素的累积权重，它是通过之前所有体素权重的指数衰减和累积来计算的。这个值可能与体素的透明度或可见性有关，用来表示体素在整个体积数据中的重要性或贡献度。

公式 $$T_i=\exp (-\sum _{j=1}^{i-1}{\sigma }_j{\delta }_j)$$ 表示体素权重是从第一个体素到当前体素的所有先前体素权重的衰减函数的累积结果。其中，$${\sigma }_j$$ 和 $${\delta }_j$$ 是与每个体素相关的参数。

调整因子 $$(1-\exp (-{\sigma }_i{\delta }_i))$$：

$${\sigma }_i$$和 $${\delta }_i$$ 是第i个体素的特定参数，可能与该体素的属性（如密度、颜色、梯度等）有关。

$$(1-\exp (-{\sigma }_i{\delta }_i))$$是一个调整因子，它用于调整第i个体素的权重。当 $${\sigma }_i{\delta }_i$$ 较大时，这个调整因子趋近于1，表明体素权重会被大幅调整；当$${\sigma }_i{\delta }_i$$ 接近0时，调整因子趋近于0，体素权重的调整较小。

综合公式：

将这两部分结合起来，$$T_i(1-\exp (-{\sigma }_i{\delta }_i))$$ 给出了第i个体素在考虑其自身特性和前 ( i-1 ) 个体素的影响后的最终权重。这个权重可以用来确定是否保留该体素。如果权重低于某个阈值，体素可能会被剪枝，也就是在3D重建中被认为是不重要的，可以被移除以节省计算资源。

这个渲染的公式怎么理解

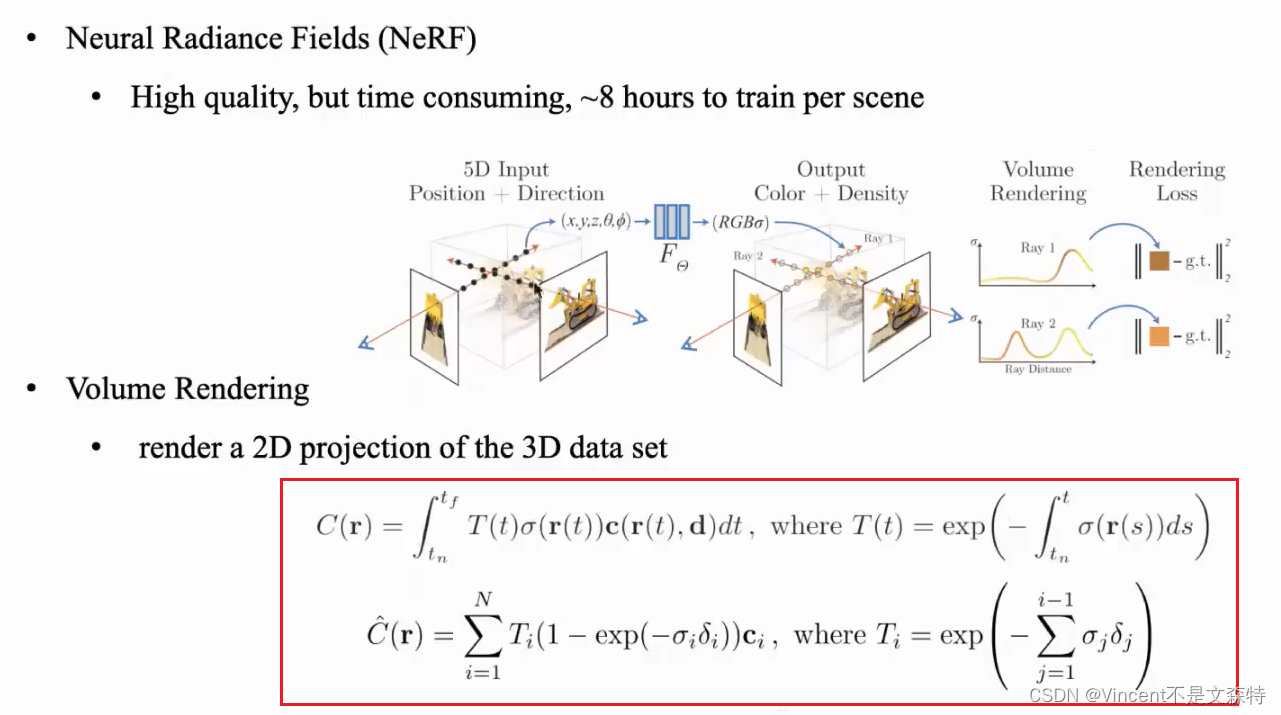
这个公式是体积渲染中的一个标准积分公式，它用于渲染3D数据集的2D投影。体积渲染是一个将3D体数据转换为2D图像的过程，通常用于医学成像、科学可视化以及计算机图形学中。下面是公式的详细解释：

$$积分公式C(r)：$$

$$C(r)是一个从体数据中沿着视线r(t)积分得到的颜色值，代表最终渲染的像素颜色。$$
$$T(t)是从视线起点t_n到当前点t的透射率，表示光线到达该点之前被体素吸收的量。它是一个衰减因子，随路径上的吸收而指数衰减。$$
$$\sigma (r(s))是体素在视线上s处的吸收系数，表示体素对光线的吸收能力。$$
$$c(r(t))是在视线上t处的体素颜色。$$
$$dt和ds是积分变量，用于积分沿视线的颜色和透射率。$$

这个积分模拟了光线穿过半透明或不透明物体时颜色的累积和衰减效果，这是体积渲染的核心。

$$离散近似公式\hat{C}(r)：$$

$$\hat{C}(r)是积分公式的离散近似，用于实际计算中。$$
$$N是视线路径上的体素数量。$$
$$T_i是第i个体素处的累积透射率。$$
$$1-\exp (-{\sigma }_i{\delta }_i)是第i个体素的局部吸收率，与体素的属性（如密度）有关。$$
$$c_i是第i个体素的颜色。$$

$$在这个离散近似中，我们把视线路径分成N个体素，并且逐个体素累加颜色值，同时考虑到每个体素的吸收和透射影响。这样可以实现在计算机中对体积数据进行有效的渲染。$$

总结来说，这些公式是体积渲染技术的基础，它们通过模拟光线通过3D体数据的传播来产生2D图像。

我对离散近似公式还是不理解，请举例说明

离散近似公式是用来从3D体积数据生成2D图像的，它通过对体积数据集中的沿视线路径的体素进行采样和累加来实现。让我们通过一个简化的例子来说明这个过程：

假设你有一个3D体积数据集，它由一系列沿某个视线排列的体素组成。每个体素具有特定的颜色和吸收率。你的目标是计算出这条视线在2D图像上的颜色。

例子：

1. 体积数据：想象一个非常简单的情况，你有一列沿视线方向的5个体素，每个体素有不同的颜色和吸收率：

   • 体素1: 颜色为蓝色，吸收率为0.1
   • 体素2: 颜色为绿色，吸收率为0.2
   • 体素3: 颜色为红色，吸收率为0.3
   • 体素4: 颜色为黄色，吸收率为0.4
   • 体素5: 颜色为紫色，吸收率为0.5

2. 累积透射率 $$T_i$$：每个体素的累积透射率表示从视线的起点到该体素前的光线透射程度。例如，体素1的透射率最高，因为它是第一个体素，没有前面的体素吸收光线；而体素5的透射率最低，因为它之前的体素都对光线有一定的吸收。

3. 局部吸收率：每个体素对光线的局部吸收率根据其吸收率来计算，例如 $$1-\exp (-{\sigma }_i{\delta }_i)$$。这个值越接近1，表示体素对光线的吸收越多。

4. 计算2D图像上的颜色：沿视线对每个体素进行迭代，将每个体素的颜色与其局部吸收率和累积透射率相乘，然后将所有这些值累加起来，得到最终的2D图像上的颜色。

具体计算过程（假设值）：

1. 对于体素1，其累积透射率 $$T_1$$ 为1（因为它是第一个体素），局部吸收率为 $$1-\exp (-0.1)$$。假设蓝色用数值0.5表示，计算得到的贡献为 $$1\times (1-\exp (-0.1))\times 0.5$$。

2. 对于体素2，累积透射率 $$T_2$$ 考虑了体素1的吸收，因此小于1。类似地，它的局部吸收率为 $$T_2\times 1-\exp (-0.2)\times 颜色对应的数值$$，并且它的颜色值（绿色）可能是0.4。

3. 依此类推，计算每个体素的颜色贡献，并将它们累加。

通过累加每个体素的贡献，你就可以得到视线在2D图像上的最终颜色。这个过程在整个体积数据集中重复进行，最终生成整个2D图像。