素数判断

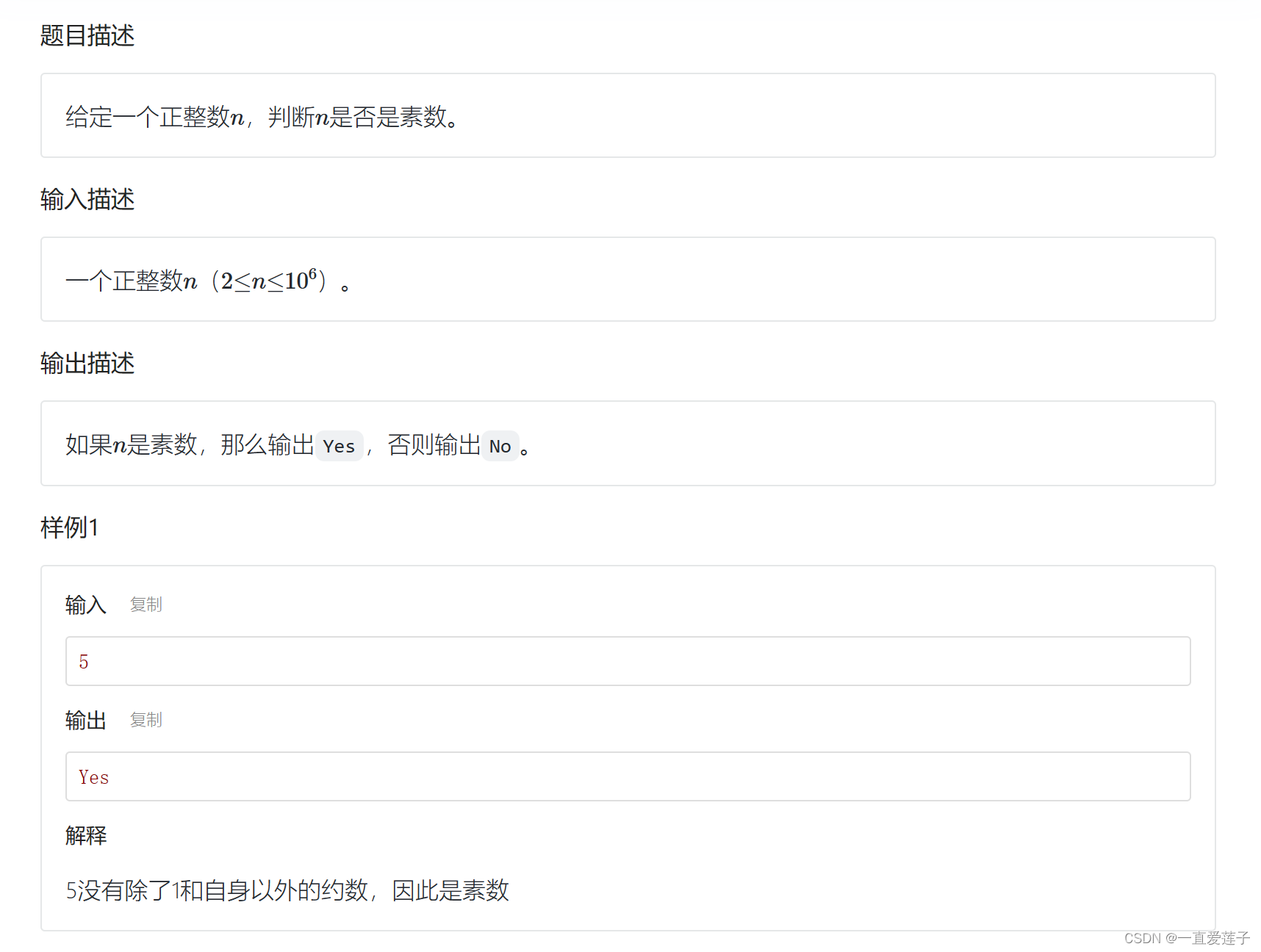
//素数
#include <cstdio>
#include <cmath>

bool isPrime(int n) 
{
    if (n <= 1) //已知一个素数判断：条件就是n是否能被2，，，，，整除，所以1且小于是不行的
    {
        return false;
    }
    int sqr = (int)sqrt(1.0 * n);//范围缩小到本身开方
    for (int i = 2; i <= sqr; i++)   
    {
        if (n % i == 0) //进行判断素数  
        {
            return false;  
        }
    }
    return true;  
}

int main() {  
    int n;  
    scanf("%d", &n);  
    printf(isPrime(n) ? "Yes" : "No");  
    return 0;  
}

打印素数表

![在这里插入图片描述]（https://img-blog.csdnimg.cn/61298fca1493407cac00d42aeadc8d97.png）

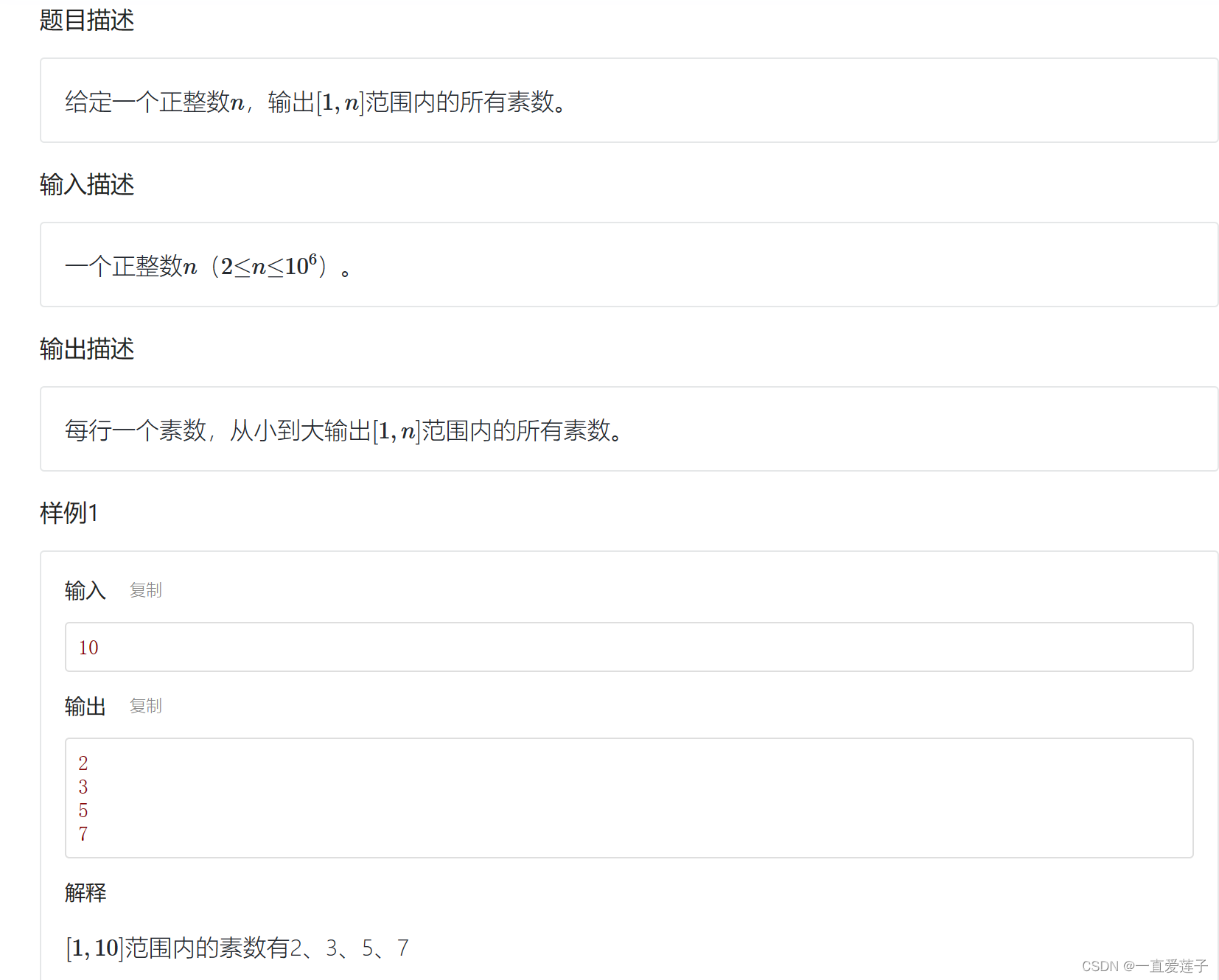
//打印素数表：
//本质是将所有数进行枚举，然后进行判断素数
//可以用布尔函数进行改变和判断

c++代码

用动态数组进行存储

#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;

const int MAXN = 1000000 + 1;
bool isPrime[MAXN];
vector<int> primes;

void getPrimes(int n) {
    memset(isPrime, true, sizeof(isPrime));
    for (int i = 2; i <= n; i++) {
        if (isPrime[i]) {
            primes.push_back(i);
            for (int j = i + i; j <= n; j += i) {
                isPrime[j] = false;    
            }
        }
    }
}

int main() {    
    int n;    
    scanf("%d", &n);    
    getPrimes(n);    
    for (int i = 0; i < primes.size(); i++) {    
        printf("%d\n", primes[i]);    
    }
    return 0;    
}

c 代码

#include<stdio.h>
#include<math.h>
bool isprime(int n)//这个就是改变布尔函数，下面用于输出素数表
{
	if (n <= 1) return false;
	int sqr = (int)sqrt(1.0 * n);
	for (int i = 2; i <= sqr; i++)
	{
		if (n % i == 0) return false;
	}
	return true;
}

int prime[101], pum = 0;
bool p[101] = { 0 };
void find_prime()//求素数表
{
	for (int i = 1; i < 101; i++)  
	{
		if (isprime(i) == true)  
		{
			prime[pum++] = i;  
			p[i] = true;  
		}
	}
}
int main()  
{
	find_prime();  
	for (int i = 0; i < pum; i++)  
	{
		printf("%d ", prime[i]);  
	}
}

最大素数

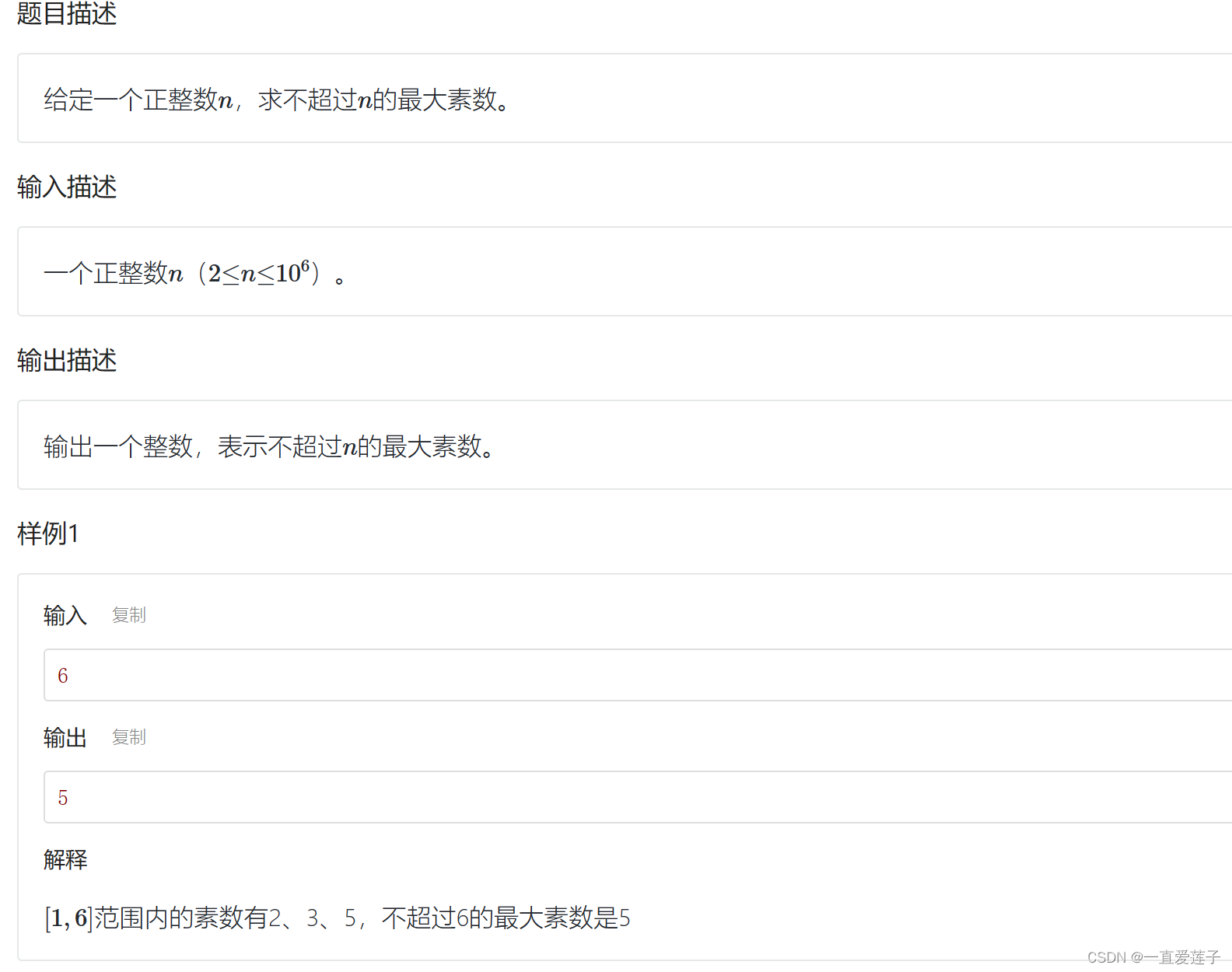
需要注意的电视：
memset(isPrime, true, sizeof(isPrime));//这个表示的是c++中的一个函数，局势对于数组进行赋值操作，后面是空间的大小

#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;


//定义数组，布尔函数，以及动态数组
const int MAXN = 1000000 + 1;
bool isPrime[MAXN];
vector<int> primes;


void getPrimes(int n) {
    memset(isPrime, true, sizeof(isPrime));

    //是素数就加入到数组中
    for (int i = 2; i <= n; i++) {
        if (isPrime[i]) {
            primes.push_back(i);   
            for (int j = i + i; j <= n; j += i) {//进行判断是不是素数，这个方法，，，还行吧，不用调用函数了



                isPrime[j] = false;   
            }
        }
    }
}

int main() {   
    int n;   
    scanf("%d", &n);   
    getPrimes(n);   
    printf("%d", primes.back());//输出最后一位   
    return 0;   
}

最小素数

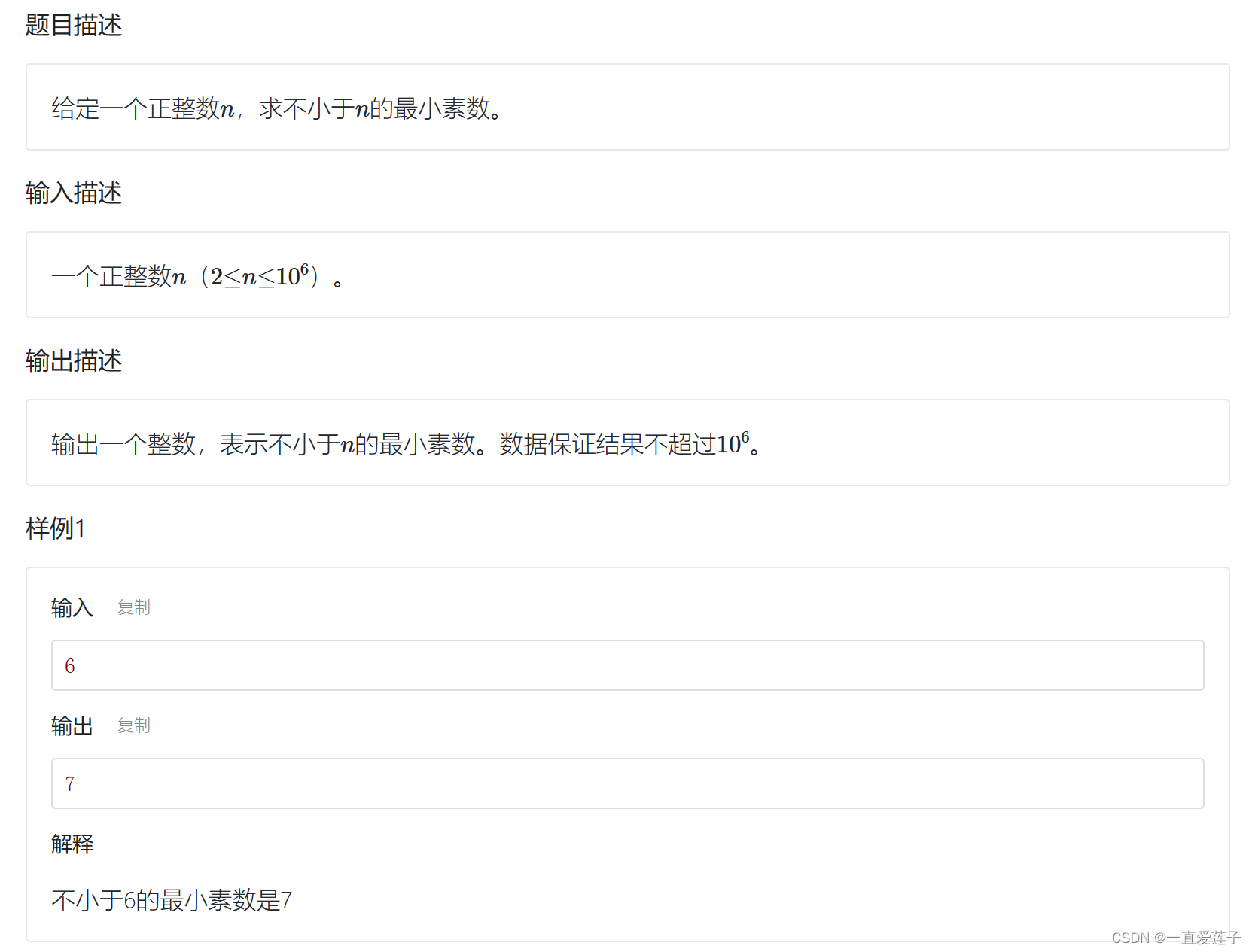
//求出大于本身数的最小素数
//这个方法是在不是一个好的方法
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;

const int MAXN = 1000000 + 1;
bool isPrime[MAXN];//布尔函数
vector<int> primes;//数组嘛



//从2开始到N存入素数
void getPrimes() {
    memset(isPrime, true, sizeof(isPrime));//对于布尔函数赋值的很好的操作
    for (int i = 2; i < MAXN; i++) {
        if (isPrime[i]) {
            primes.push_back(i);
            for (int j = i + i; j < MAXN; j += i) {
                isPrime[j] = false;
            }
        }
    }
}


int main() {  
    int n;  
    scanf("%d", &n);  

    getPrimes();  

    //输出一开始的数就是最小  
    for (int i = 0; i < primes.size(); i++) {  
        if (primes[i] >= n) {  
            printf("%d", primes[i]);  
            break;  
        }
    }
    return 0;  
}

孪生素数

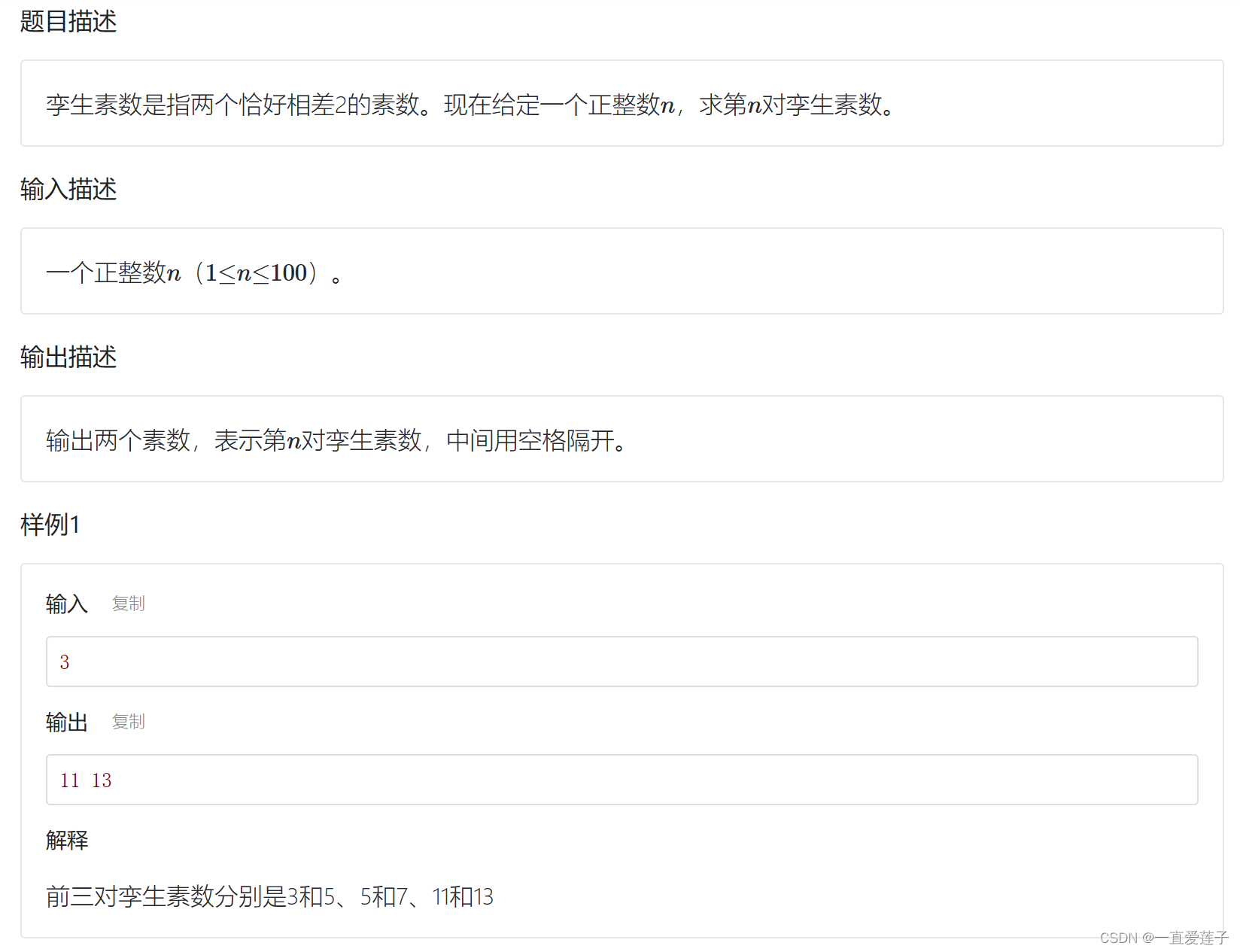
每次k和k+2都是素食，所有只要考虑的是截止的是第几个就行了

int getTwinPrime(int n) {
    int k = 1;
    for (int i = 0; i < n; i++) {
        do {
            k += 2;
        } while (!isPrime(k) || !isPrime(k + 2));
    }
    return k;
}

整体的代码是

#include <cstdio>
#include <cmath>

bool isPrime(int n) {
    if (n <= 1) {
        return false;
    }
    int sqr = (int)sqrt(1.0 * n);
    for (int i = 2; i <= sqr; i++) {
        if (n % i == 0) {
            return false;
        }
    }
    return true;
}

int getTwinPrime(int n) {
    int k = 1;
    for (int i = 0; i < n; i++) {
        do {
            k += 2;
        } while (!isPrime(k) || !isPrime(k + 2));
    }
    return k;
}

int main() {
    int n;
    scanf("%d", &n);
    int twinPrime = getTwinPrime(n);
    printf("%d %d", twinPrime, twinPrime + 2);
    return 0;
}