算法笔记-第九章-二叉树的遍历（未完成-还要搞）

news2024/10/7 12:22:22

算法笔记-第九章-二叉树的遍历

  • 二叉树的先序遍历
  • 二叉树的中序遍历
  • 二叉树的后序遍历
  • 二叉树的层次遍历
    • 注意点一：
    • 注意点二：
  • 二叉树的高度
  • 二叉树的结点层号
  • 翻转二叉树
    • 翻转二叉树不同的方法
      • 方法一：用栈实现
      • 方法二：用队列实现
      • 方法三：

二叉树的先序遍历

在这里插入图片描述
在这里插入图片描述

//二叉树的先序遍历
#include <cstdio>
#include <vector>
using namespace std;

const int MAXN = 50;

struct Node //用结构体表示左子树和右子树的数据
{
    int l, r;
} nodes[MAXN];

vector<int> pre;//设置一个数组用来存储先序遍历的数据

void preOrder(int root) 
{
    if (root == -1) 
    {
        return;
    }
    pre.push_back(root);
    preOrder(nodes[root].l);//用递归的方式将输入的左子树和右子树都进行重新判断，然后输入到数组当中
    preOrder(nodes[root].r);
}

int main() 
{
    int n;
    scanf("%d", &n);

    for (int i = 0; i < n; i++) 
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);  
    }

    preOrder(0);//直接将头结构体带入  

    //输出数组中数据  
    for (int i = 0; i < (int)pre.size(); i++)   
    {
        printf("%d", pre[i]);  
        if (i < (int)pre.size() - 1)   
        {
            printf(" ");  
        }
    }
    return 0;  
}

二叉树的中序遍历

在这里插入图片描述
在这里插入图片描述

//思路还是递归的思路
#include <cstdio>
#include <vector>
using namespace std;

const int MAXN = 50;

struct Node 
{
    int l, r;
} nodes[MAXN];

vector<int> in;

//思路其实就是利用递归遍历左中右，然后存入到数组当中
void inOrder(int root)
{
    if (root == -1) 
    {
        return;
    }
    inOrder(nodes[root].l);
    in.push_back(root);
    inOrder(nodes[root].r);
}
//主要是一个函数就是主要的


int main() 
{
    int n;
    scanf("%d", &n);  
    for (int i = 0; i < n; i++)   
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);  
    }
    inOrder(0);  
    for (int i = 0; i < (int)in.size(); i++)   
    {
        printf("%d", in[i]);  
        if (i < (int)in.size() - 1)  
        {
            printf(" ");  
        }
    }
    return 0;  
}

二叉树的后序遍历

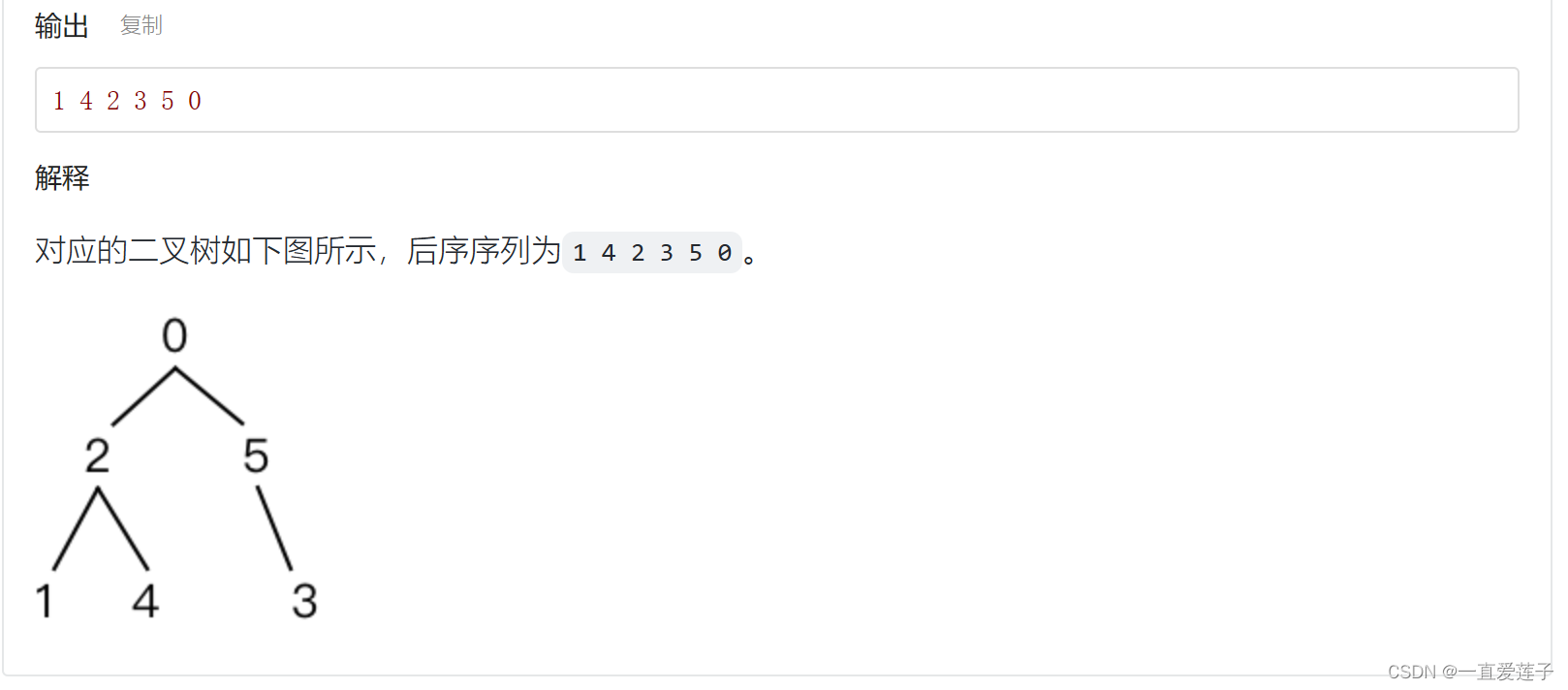
在这里插入图片描述
在这里插入图片描述

//这道题目因为还是用递归的方式进行的，所以还是
//简答用递归左右中的方式进行
#include <cstdio>
#include <vector>
using namespace std;

const int MAXN = 50;

struct Node {
    int l, r;
} nodes[MAXN];

vector<int> post;

void postOrder(int root) {
    if (root == -1) {
        return;
    }
    postOrder(nodes[root].l);
    postOrder(nodes[root].r);
    post.push_back(root);
}

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) { 
        scanf("%d%d", &nodes[i].l, &nodes[i].r); 
    }
    postOrder(0);   
    for (int i = 0; i < (int)post.size(); i++) {   
        printf("%d", post[i]);   
        if (i < (int)post.size() - 1) {   
            printf(" ");   
        }
    }
    return 0;   
}

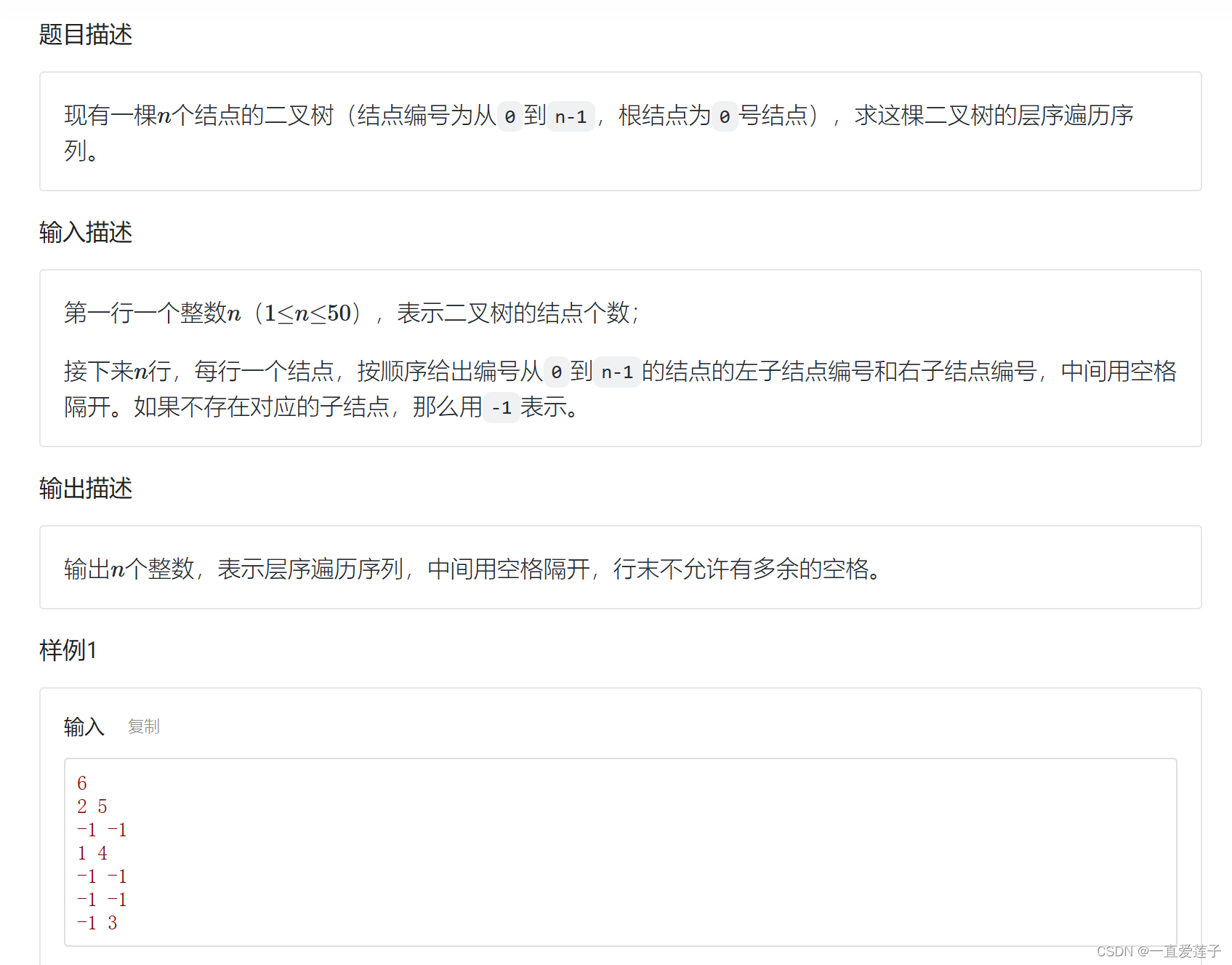
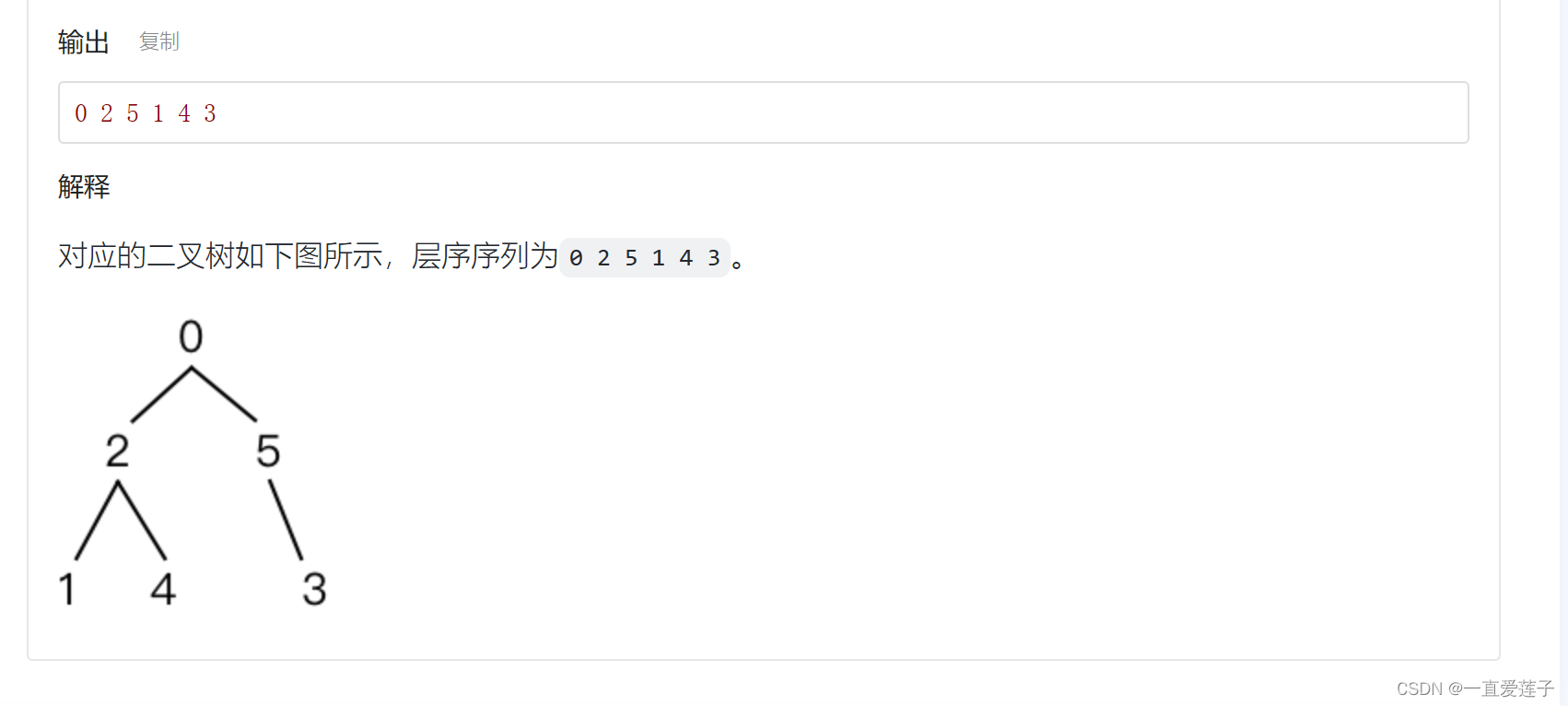
二叉树的层次遍历

在这里插入图片描述

在这里插入图片描述

#include <cstdio>
#include <vector>
#include <queue>
using namespace std;

const int MAXN = 50;

struct Node 
{
    int l, r;
} nodes[MAXN];


vector<int> layer;

//就是根据遍历的思路来就好
void layerOrder(int root) 
{
    queue<int> q;
    q.push(root);
    while (!q.empty())
    {
        int front = q.front();//去除首元素
        q.pop();//删除首元素


        layer.push_back(front);
        //加入到队列中

        if (nodes[front].l != -1)
        {
            q.push(nodes[front].l);
        }

        if (nodes[front].r != -1) 
        {
            q.push(nodes[front].r);
        }
    }
}



int main() 
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) 
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);
    }
    layerOrder(0);
    //输入首地址0
    for (int i = 0; i < (int)layer.size(); i++
    {
        printf("%d", layer[i]);
        if (i < (int)layer.size() - 1) 
        {
            printf(" ");
        }
    }
    return 0;
}

注意点一：

queue q;和queue<node*> q两者之间的区别是
一个是不可以改变队列中的元素的，一个数带入的时候就是可以直接改变原函数的

注意点二：

层次遍历使用的是队列，基本思路是
访问root，加入队列
如果有左节点，加入左节点
如果有右节点，加入右节点//这里就是要递归方式进行了，
//然后重新进行放问(当然是要用while)

二叉树的高度

在这里插入图片描述
在这里插入图片描述

//二叉树的高度
//题目本身就是简单的递归遍历
#include <cstdio>
#include <algorithm>
using namespace std;

const int MAXN = 50;

struct Node 
{
    int l, r;
} nodes[MAXN];

int getHeight(int root) 
{
    if (root == -1) 
    {
        return 0;
    }
    int leftHeight = getHeight(nodes[root].l);
    int rightHeight = getHeight(nodes[root].r);
    return max(leftHeight, rightHeight) + 1;
}





int main()   
{
    int n;  
    scanf("%d", &n);  
    for (int i = 0; i < n; i++)   
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);  
    }
    printf("%d", getHeight(0));  
    return 0;  
}

二叉树的结点层号

在这里插入图片描述
在这里插入图片描述

#include <cstdio>
#include <vector>
#include <queue>
using namespace std;

const int MAXN = 50;

struct Node 
{
    int l, r;
} nodes[MAXN];

int layers[MAXN];



void layerOrder(int root) 
{
    queue<int> q;
    q.push(root);
    int layer = 1;
    while (!q.empty())
    {
        int cnt = q.size();//一层中有多少个结点

        for (int i = 0; i < cnt; i++) 
        {
            int front = q.front();
            q.pop();

            layers[front] = layer;//结点代表的层数

            //
            if (nodes[front].l != -1) 
            {
                q.push(nodes[front].l);
            }

            if (nodes[front].r != -1) 
            {
                q.push(nodes[front].r);
            }

        }
        layer++;//一层一层的来
    }
}


int main() 
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) 
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);
    }

    layerOrder(0);  

    for (int i = 0; i < n; i++)  
    {
        printf("%d", layers[i]);  
        if (i < n - 1)  
        {
            printf(" ");  
        }
    }
    return 0;  
}

翻转二叉树

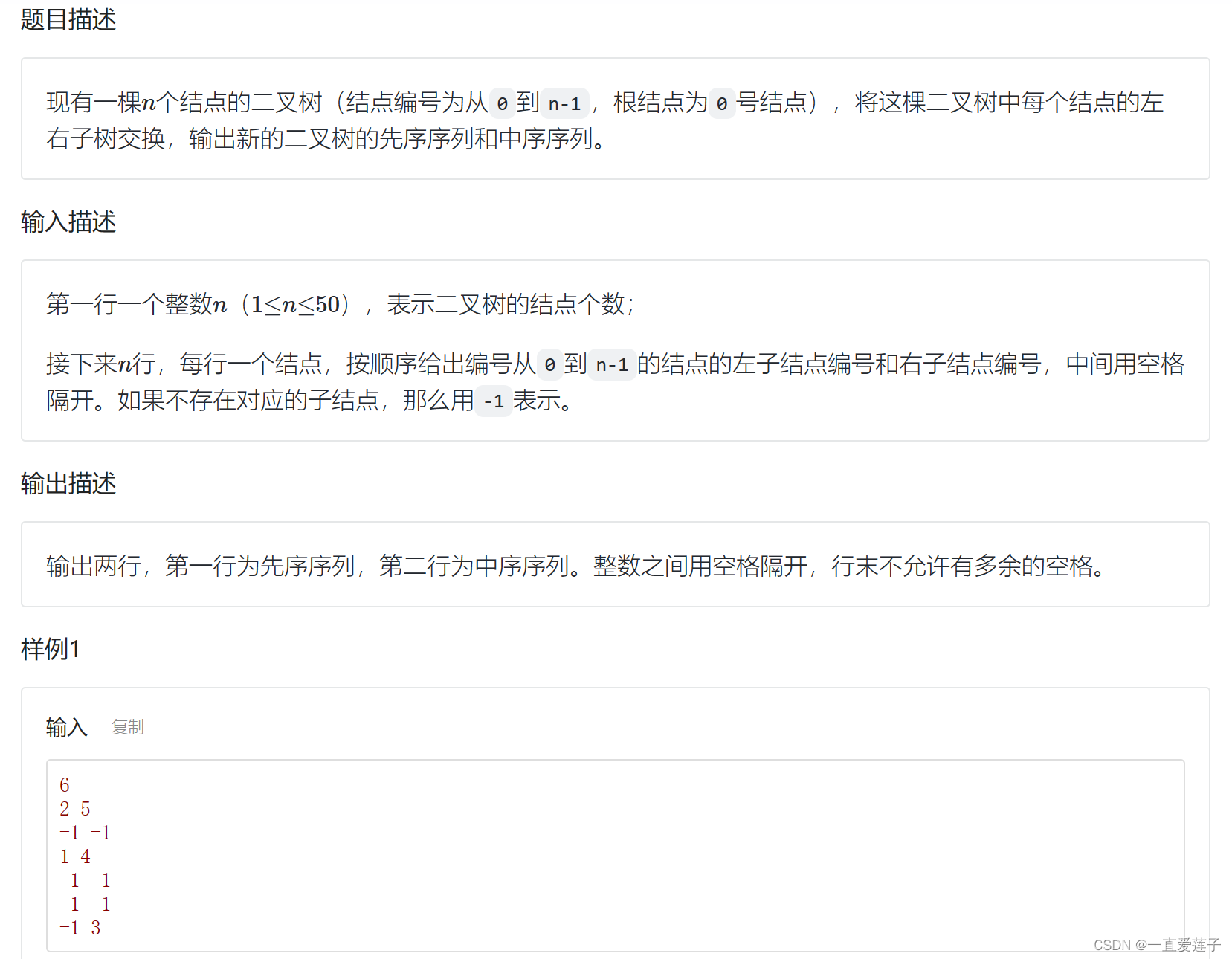
在这里插入图片描述

在这里插入图片描述
本题就是使用了递归的思路进行翻转二叉树，
再设置两个数组进行遍历二叉树然后输入到数组当中


#include <cstdio>
#include <vector>
#includ e <algorithm>
using namespace std;

const int MAXN = 50;

struct Node
{
    int l, r;
} nodes[MAXN];

vector<int> pre, in, post;//

void preOrder(int root)
{
    if (root == -1) 
    {
        return;
    }
    pre.push_back(root);
    preOrder(nodes[root].l);
    preOrder(nodes[root].r);
}

void inOrder(int root) 
{
    if (root == -1) 
    {
        return;
    }
    inOrder(nodes[root].l);
    in.push_back(root);
    inOrder(nodes[root].r);
}

void revert(int root) //利用的递归将左右孩子节点分别翻转
{
    if (root == -1) 
    {
        return;
    }
    revert(nodes[root].l);
    revert(nodes[root].r);
    swap(nodes[root].l, nodes[root].r);
}


int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) 
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);
    }



    revert(0);//用递归的思想进行翻转

    preOrder(0);//也都是用递归的思路将二叉树的数据存储到数组当中
    inOrder(0);

    for (int i = 0; i < (int)pre.size(); i++) //先序遍历
    {
        printf("%d", pre[i]);
        if (i < (int)pre.size() - 1) 
        {
            printf(" ");
        }
    }

    printf("\n");

    for (int i = 0; i < (int)in.size(); i++) 
    {
        printf("%d", in[i]);
        if (i < (int)in.size() - 1)
        {
            printf(" ");
        }
    }
    return 0;
}

翻转二叉树不同的方法

在这里插入图片描述

方法一：用栈实现

思路：左右节点进行交换，循环翻转每个节点的左右子节点，将未翻转的子节点存入栈中，循环直到栈里所有节点都循环交换完为止

public TreeNode invertTree(TreeNode root)
{
    if (root == null)//开始进行判断是否为空
    {
        return null;
    }
    Stack<TreeNode> stack = new Stack<>();//设置一个栈


    stack.push(root);//将根节点进行入栈

    while (!stack.isEmpty())
    {
        final TreeNode node = stack.pop();//出栈进行访问和翻转孩子结点

        final TreeNode left = node.left;
        node.left = node.right;
        node.right = left;  

        //下面：从内到外进行翻转，所有先将右变的节点进行入栈，然后进行翻转，然后再是左边的    
        if (node.left != null)      
        {
            stack.push(node.left);      
        }
        if (node.right != null)       
        {
            stack.push(node.right);      
        }
    }
    return root;      
}

方法二：用队列实现

/用队列实现
//队列和栈的思路是一样的，都是根据进行入队和出队进行的

public TreeNode invertTree(TreeNode root) {
    if (root == null) {
        return null;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);  
    while (!queue.isEmpty()) {  

        TreeNode node = queue.poll();    

        TreeNode left = node.left;    
        node.left = node.right;    
        node.right = left;    

        if (node.left != null) {    
            queue.offer(node.left);    
        }
        if (node.right != null) {    
            queue.offer(node.right);    
        }
    }
    return root;    
}

方法三：

因为翻转所有的节点的孩子都是翻转左右节点，
所有在递归的思路中=确立了节点，用前序的思路直接遍历和
翻转二叉树,知道节点为NULL

public TreeNode invertTree(TreeNode node) {
    if (node == null) {
        return null;
    }
    TreeNode temp = node.left;
    node.left = node.right;
    node.right = temp;
    invertTree(node.left);
    invertTree(node.right);
    return node;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1213851.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

深度学习之基于Pytorch和OCR的识别文本检测系统

深度学习之基于Pytorch和OCR的识别文本检测系统

欢迎大家点赞、收藏、关注、评论啦 &#xff0c;由于篇幅有限&#xff0c;只展示了部分核心代码。 文章目录 一项目简介深度学习与OCRPyTorch在OCR中的应用文本检测系统的关键组成部分1. 图像预处理2. 深度学习模型3. 文本检测算法4. 后处理 二、功能三、系统四. 总结 一项目简…
阅读更多...
git clone:SSL: no alternative certificate subject name matches target host name

git clone:SSL: no alternative certificate subject name matches target host name

git clone 时的常见错误&#xff1a; fatal: unable to access ‘https://ip_or_domain/xx/xx.git/’: SSL: no alternative certificate subject name matches target host name ‘ip_or_domain’ 解决办法&#xff1a; disable ssl verify git config --global http.sslVe…
阅读更多...
基于 Amazon EKS 搭建开源向量数据库 Milvus

基于 Amazon EKS 搭建开源向量数据库 Milvus

一、前言 生成式 AI&#xff08;Generative AI&#xff09;的火爆引发了广泛的关注&#xff0c;也彻底点燃了向量数据库&#xff08;Vector Database&#xff09;市场&#xff0c;众多的向量数据库产品开始真正出圈&#xff0c;走进大众的视野。 根据 IDC 的预测&#xff0c;…
阅读更多...
基于STC12C5A60S2系列1T 8051单片机的数模芯片TLC5615实现数模转换应用

基于STC12C5A60S2系列1T 8051单片机的数模芯片TLC5615实现数模转换应用

基于STC12C5A60S2系列1T 8051单片的数模芯片TLC5615实现数模转换应用 STC12C5A60S2系列1T 8051单片机管脚图STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式及配置STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式介绍数模芯片TLC5615介绍通过按键调节数模芯片TLC5615…
阅读更多...
低代码编辑平台后台实现

低代码编辑平台后台实现

背景 之前做过一个前端低代码编辑平台&#xff0c;可以实现简单的移动端页面组件拖拽编辑&#xff1a; https://github.com/li-car-fei/react-visual-design 最近基于C的oatpp框架实现了一下后台。使用oatpp框架做web后台开发时&#xff0c;发现按照官方的示例使用的话&#…
阅读更多...
SSH远程登录协议

SSH远程登录协议

目录 什么是ssh服务器 概念 优点 原理 SSH登录 方法一 无需验证 方法二 格式&#xff1a; ssh -l 用户名 IP 地址 -p port -l &#xff1a;指定登录名称 -p&#xff1a;选项&#xff0c;指定登录端口&#xff08;当服务端的端口非默认时&#xff0c;需要使用-p…
阅读更多...
拿到信创天翼云电脑账号后，我又傻眼了...

拿到信创天翼云电脑账号后，我又傻眼了...

在《面向国产系统的 App 发布&#xff0c;含泪总结》中&#xff0c;我就吐槽过信创产品的不靠谱。用户购买一台终端&#xff0c;都没法用&#xff0c;得经历复杂的账号申请。 紧催慢催&#xff0c;等待了半个月之后&#xff0c;今天终于拿到了账号。然而&#xff0c;满怀期待登…
阅读更多...
OpenAI与微软合作，构建 ChatGPT 5 模型；10天准确天气预报

OpenAI与微软合作，构建 ChatGPT 5 模型；10天准确天气预报

&#x1f989; AI新闻 &#x1f680; OpenAI与微软合作&#xff0c;构建 ChatGPT 5 模型&#xff0c;下一代人工智能或拥有超级智能 摘要&#xff1a;OpenAI首席执行官 Sam Altman 在接受采访时表示&#xff0c;OpenAI正在与微软合作构建下一代人工智能模型 ChatGPT 5&#x…
阅读更多...
Django——模板层、模型层

Django——模板层、模型层

模板层 一. 模版语法 {{ }}: 变量相关 {% %}: 逻辑相关 1. 注释是代码的母亲 {# ... #} 2. 基本数据类型传值 int1 123 float1 11.11 str1 我也想奔现 bool1 True list1 [小红, 姗姗, 花花, 茹茹] tuple1 (111, 222, 333, 444) dict1 {username: jason, age: 18, i…
阅读更多...
rpmbuild 包名 version 操作系统信息部分来源 /etc/rpm/macros.dist

rpmbuild 包名 version 操作系统信息部分来源 /etc/rpm/macros.dist

/etc/rpm/macros.dist openeuler bclinux src.rpm openssl-1.1.1f-13.oe1.src.rpm 打包名称结果 openeuler openssl-1.1.1f-13.aarch64.rpm bclinux openssl-1.1.1f-13.oe1.bclinux.aarch64.rpm 验证 修改openeuler配置文件macros.dist 重新在openeuler上执行rpmbuild…
阅读更多...
第三章 栈和队列【24王道数据结构笔记】

第三章 栈和队列【24王道数据结构笔记】

1.栈 1.1 栈的基本概念 只允许在一端(栈顶top)进行插入或删除操作的受限的线性表。后进先出&#xff08;Last In First Out&#xff09;LIFO。或者说先进后出FILO。 进栈顺序&#xff1a;a1 > a2 > a3 > a4 > a5出栈顺序&#xff1a;a5 > a4 > a3 > a2 …
阅读更多...
数据结构—LinkedList与链表

数据结构—LinkedList与链表

目录 一、链表 1. 链表的概念及结构 1. 单向或者双向 2. 带头或者不带头 3. 循环或者非循环 二.LinkedList的使用 1.LinkedList概念及结构 2. LinkedList的构造 3. LinkedList的方法 三. ArrayList和LinkedList的区别 一、链表 1. 链表的概念及结构 链表是一种 物理…
阅读更多...
Postman实现接口的文件上传

Postman实现接口的文件上传

近期在复习Postman的基础知识&#xff0c;在小破站上跟着百里老师系统复习了一遍&#xff0c;也做了一些笔记&#xff0c;希望可以给大家一点点启发。 接口的文件上传&#xff0c;与其他接口的传参差不多&#xff0c;只要点击form-data&#xff0c;选择要上传的文件即可。 实际…
阅读更多...
Java第十九章

Java第十九章

一.绘制图形 Java 可以分别使用 Graphics类和Graphics2D 类绘制图形&#xff0c;Graphics 类使用不同的方法实现不同图形的绘制。例如&#xff0c;drawLine()方法可以绘制直线&#xff0c;drawRect()方法用于绘制矩形&#xff0c;drawOval()方法用于绘制椭圆形等。 例1. 例2. …
阅读更多...
物联网项目：充电桩项目实战~

物联网项目：充电桩项目实战~

你好&#xff0c;我是田哥 最近除了忙于面试辅导、模拟面试以外&#xff0c;还在搞一件大事&#xff1a;充电桩项目。 分布式微服务项目实战&#xff1a;充电桩项目 充电桩项目肯定是和物联网相关的&#xff0c;聊到物联网又不得不聊的是MQTT协议。 什么是MQTT MQTT&#xff0c…
阅读更多...
数据结构前言（空间复杂度）

数据结构前言（空间复杂度）

1.空间复杂度 空间复杂度也是一个数学表达式&#xff0c;是对一个算法在运行过程中临时占用存储空间大小的量度 。 空间复杂度不是程序占用了多少bytes的空间&#xff0c;因为这个也没太大意义&#xff0c;所以空间复杂度算的是变量的个数。 空间复杂度计算规则基本跟实践复杂…
阅读更多...
解决Github上的README无法显示图片

解决Github上的README无法显示图片

首先感谢博主的思路&#xff1a;思路 最近写了点东西提交到git 发现本地能查看md里的图片用的相对路径&#xff0c;提交到github就看不见&#xff0c;并且发现不只是我自己的仓库看不见&#xff0c;其他人的我也看不见。那就有问题了 解决&#xff1a;正常使用相对路径&…
阅读更多...
C#中.NET Framework4.8 Windows窗体应用通过EF访问新建数据库

C#中.NET Framework4.8 Windows窗体应用通过EF访问新建数据库

目录 一、 操作步骤 二、编写EF模型和数据库上下文 三、 移植&#xff08;Migrations&#xff09;数据库 四、编写应用程序 五、生成效果 前文已经说过.NET Framework4.8 控制台应用通过EF访问已经建立的和新建的数据库。 本文想说的是&#xff0c;.NET Framework4.8 Win…
阅读更多...
黑豹程序员-SpringCloudAlibaba聚合工程打包和运行

黑豹程序员-SpringCloudAlibaba聚合工程打包和运行

文章目录 1、SpringCloudAlibaba项目结构2、打包配置3、打包4、运行 1、SpringCloudAlibaba项目结构 2、打包配置 3、打包 4、运行 java -jar rms-parent.jar
阅读更多...
解决：java: 错误: 不支持发行版本 5 最有效方法

解决：java: 错误: 不支持发行版本 5 最有效方法

报错信息如图&#xff1a; 直接上终极方法&#xff1a; 修改配置文件 如图找到settings.xml文件 在标签中间插入如下代码&#xff08;jdk更改为自己电脑上的版本&#xff09; <profile><id>development</id><activation><jdk>11</jdk><…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023