git clone 时的常见错误:
- fatal: unable to access ‘https://ip_or_domain/xx/xx.git/’: SSL: no alternative certificate subject name matches target host name ‘ip_or_domain’

解决办法: disable ssl verify
git config --global http.sslVerify false
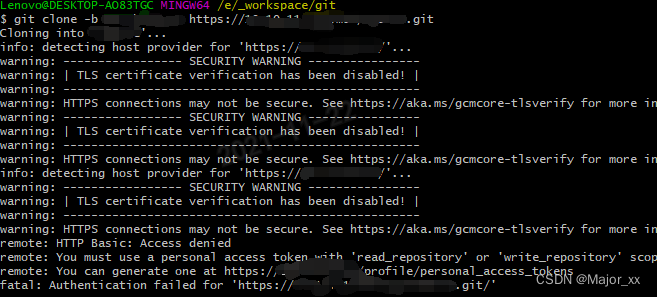
- remote: HTTP Basic: Access denied
remote: You must use a personal access token with ‘read_repository’ or ‘write_repository’ scope for Git over HTTP.
remote: You can generate one at https://ip_or_domain/profile/personal_access_tokens
fatal: Authentication failed for ‘https://ip_or_domain/xxx/xxx.git/’
解决办法:生成access token
按提示进入 https://ip_or_domain/profile/personal_access_tokens ip_or_domain 是你具体项目的地址
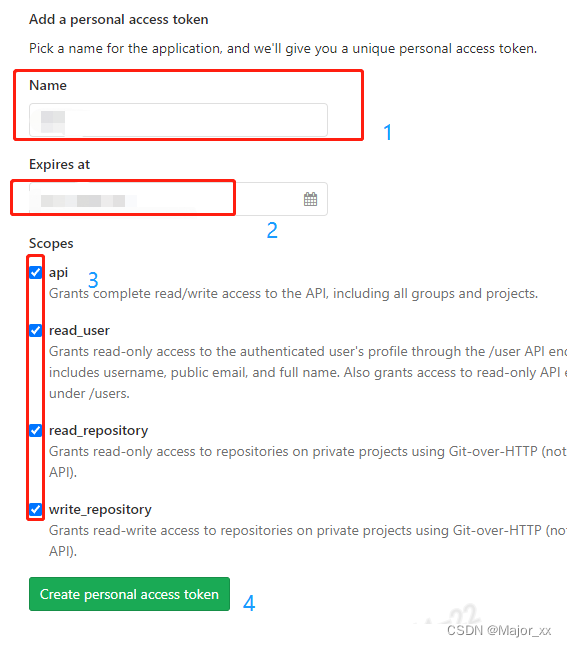
git clone 时,需要输入密码的地方, 输入你生成的 access token