第三章 栈和队列【24王道数据结构笔记】

news2024/10/7 14:22:19

1.栈

1.1 栈的基本概念

  • 只允许在一端(栈顶top)进行插入或删除操作的受限的线性表。
  • 后进先出（Last In First Out）LIFO。或者说先进后出FILO。

  

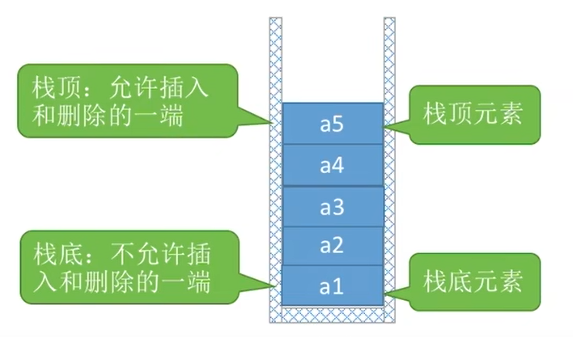
进栈顺序：a1 > a2 > a3 > a4 > a5
出栈顺序：a5 > a4 > a3 > a2 > a1 

 1.2 栈的基本操作


InitStack(&S)：初始化栈。构造一个空栈 S，分配内存空间。
DestroyStack(&S)：销毁栈。销毁并释放栈 S 所占用的内存空间。
Push(&S, x)：进栈。若栈 S 未满，则将 x 加入使其成为新的栈顶元素。
Pop(&S, &x)：出栈。若栈 S 非空，则弹出（删除）栈顶元素，并用 x 返回。
GetTop(S, &x)：读取栈顶元素。若栈 S 非空，则用 x 返回栈顶元素。
StackEmpty(S)：判空。断一个栈 S 是否为空，若 S 为空，则返回 true，否则返回 false。

1.2.1 栈的顺序存储实现

 【顺序栈的定义】

#define MaxSize 10              //定义栈中元素的最大个数
 
typedef struct{
    ElemType data[MaxSize];     //静态数组存放栈中元素
    int top;                    //栈顶元素
}SqStack;
 
void testStack(){
    SqStack S;                 //声明一个顺序栈(分配空间)
                               //连续的存储空间大小为 MaxSize*sizeof(ElemType)
}

 【顺序栈的初始化】

#define MaxSize 10
typedef struct{   
	ElemType data[MaxSize];    
    int top;
}SqStack;
 
// 初始化栈顶为-1，栈顶指针指向栈顶
void InitStack(SqStack &S){ 
    S.top = -1;                   //初始化栈顶指针
}
 
// 判断栈是否为空
bool StackEmpty(SqStack S){    
    if(S.top == -1)        
        return true;    
    else        
        return false;
}

// 初始化栈顶为0，栈顶指针指向栈顶的下一个空位
void InitStack(SqStack &S){ 
    S.top = 0;                   //初始化栈顶指针
}
 
// 判断栈是否为空
bool StackEmpty(SqStack S){    
    if(S.top == 0)        
        return true;    
    else        
        return false;
}

 【顺序栈的入栈出栈】

初始化为-1时
// 新元素进栈
bool Push(SqStack &S, ElemType x){    
    if(S.top == MaxSize - 1)   // 判断栈是否已满         
        return false;    
    S.data[++S.top] = x;    
    return true;
}
 
// 出栈
bool Pop(SqStack &x, ElemType &x){     
    if(S.top == -1)  // 判断栈是否为空         
        return false;    
    x = S.data[S.top--];    
    return true;
}

初始化为0时
// 新元素进栈
bool Push(SqStack &S, ElemType x){    
    if(S.top == MaxSize)   // 判断栈是否已满         
        return false;    
    S.data[S.top++] = x;    
    return true;
}
 
// 出栈
bool Pop(SqStack &x, ElemType &x){     
    if(S.top == 0)  // 判断栈是否为空         
        return false;    
    x = S.data[--S.top];    
    return true;
}

【读取栈顶元素】 

// 读栈顶元素
初始化为-1时
bool GetTop(SqStack S, ElemType &x){        
    if(S.top == -1) 先判空，非空读取才有意义               
        return false;        
    x = S.data[S.top];        
    return true; 
}

初始化为-1时
bool GetTop(SqStack S, ElemType &x){        
    if(S.top == 0)                
        return false;        
    x = S.data[S.top-1];        
    return true; 
}

 【读取栈的长度】 

// 获取当前栈长
当初始化为-1
int GetSize(SqStack S){        
    return S.top + 1; 
}

当初始化为0
int GetSize(SqStack S){        
    return S.top; 
}

共享栈(两个栈共享同一片空间)】

  • 共享栈--特殊的顺序栈
  • 将栈底设计在共享空间的两端，栈顶向中间靠拢
#define MaxSize 10         //定义栈中元素的最大个数
 
typedef struct{
    ElemType data[MaxSize];       //静态数组存放栈中元素
    int top0;                     //0号栈栈顶指针
    int top1;                     //1号栈栈顶指针
}ShStack;
 
//初始化栈
void InitSqStack(ShStack &S){
    S.top0 = -1;        //初始化栈顶指针
    S.top1 = MaxSize;   
}

1.2.2 栈的链式存储

【链栈的定义】

  • 定义：采用链式存储的栈称为链栈。
  • 优点：链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。
  • 特点：进栈和出栈都只能在栈顶一端进行(链头作为栈顶)

链表的头部作为栈顶，意味着：

  • 1. 在实现数据"入栈"操作时，需要将数据从链表的头部插入；
  • 2. 在实现数据"出栈"操作时，需要删除链表头部的首元节点；

因此，链栈实际上就是一个只能采用头插法插入或删除数据的链表;
栈的链式存储结构可描述为：

【链栈的定义】

typedef struct Linknode{        
    ElemType data;        //数据域    
    Linknode *next;       //指针域
}Linknode,*LiStack;
 
void testStack(){   
    LiStack L;            //声明一个链栈
}

【链栈的初始化】

typedef struct Linknode{       
    ElemType data;      
    Linknode *next;
}Linknode,*LiStack;
 
// 初始化栈
bool InitStack(LiStack &L){    // 生成虚拟头节点，并将其next指针置空
    L = (Linknode *)malloc(sizeof(Linknode));   
    if(L == NULL)             
        return false;   
    L->next = NULL;    
    return true;
}
 
// 判断栈是否为空
bool isEmpty(LiStack &L){    
    if(L->next == NULL)      
        return true;   
    else           
        return false;
}

【入栈出栈】

// 新元素入栈
bool pushStack(LiStack &L,ElemType x){  
    Linknode *s = (Linknode *)malloc(sizeof(Linknode));  
    if(s == NULL)         
        return false;   
    s->data = x;     
    // 头插法      
    s->next = L->next;  
    L->next = s;     
    return true;
}
 
// 出栈
bool popStack(LiStack &L, int &x){     
    // 栈空不能出栈  
    if(L->next == NULL)     
        return false;    
    Linknode *s = L->next;  
    x = s->data;       
    L->next = s->next;
    free(s);
    s = NULL;       
    return true;
}

 2. 队列

2.1 队列的基本概念

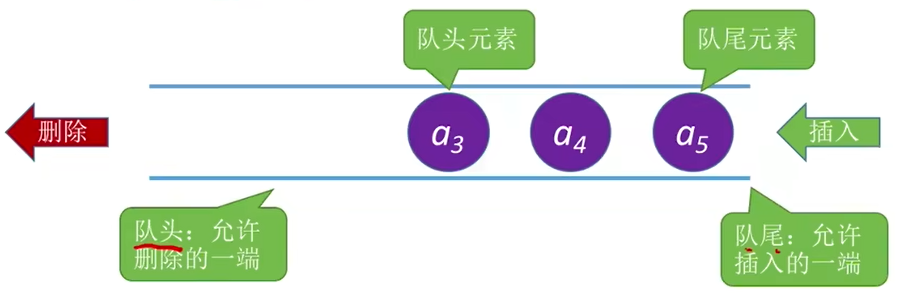
  • 只允许在表的一端(队尾)插入，表的另一端(队头)进行删除操作的受限的线性表。
  • 特点：先进先出（先入队的元素先出队）、FIFO（First In First Out）,后入后出LILO。
 

 

2.2 队列的基本操作
 


InitQueue(&Q)：初始化队列，构造一个空队列Q。
QueueEmpty(Q)：判队列空，若队列Q为空返回true，否则返回false。
EnQueue(&Qx)：入队，若队列Q未满，则将x加入使之成为新的队尾。
DeQueue(&Q&x)：出队，若队列Q非空，则删除队头元素，并用x返回。
GetHead(Q&x)：读队头元素，若队列Q非空则用x返回队头元素。
ClearQueue(&Q)：销毁队列，并释放队列Q占用的内存空间。
【队列的顺序存储实现 】
 

队头指针：指向队头元素
队尾指针：指向队尾元素或者队尾的下一个位置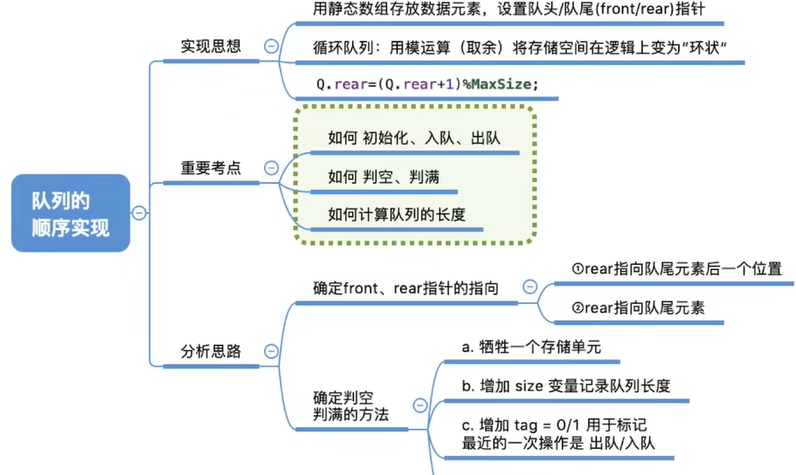
 

【顺序队列的定义】
 

#define MaxSize 10;     //定义队列中元素的最大个数
 
typedef struct{     
    ElemType data[MaxSize];   //用静态数组存放队列元素     
    int front, rear;          //队头指针和队尾指针
}SqQueue;
 
void test{     
    SqQueue Q;                //声明一个队列
}
 

【顺序队列的初始化】
 

#define MaxSize 10;
 
typedef struct{   
    ElemType data[MaxSize];  
    int front, rear;
}SqQueue;
 
// 初始化队列
void InitQueue(SqQueue &Q){    
    // 初始化时，队头、队尾指针指向0   
    // 队尾指针指向的是即将插入数据的数组下标  
    // 队头指针指向的是队头元素的数组下标
    Q.rear = Q.front = 0;
}
 
// 判断队列是否为空
bool QueueEmpty(SqQueue Q){     
    if(Q.rear == Q.front)            
        return true;   
    else          
        return false;
}
 

【入队出队（循环队列）】
 

// 新元素入队
bool EnQueue(SqQueue &Q, ElemType x){       
    // 如果队列已满直接返回
    if((Q.rear+1)%MaxSize == Q.front) 	//牺牲一个单元区分队空和队满   
        return false;    
    Q.data[Q.rear] = x;   
    Q.rear = (Q.rear+1)%MaxSize; 
    return true;
}
 
// 出队
bool DeQueue(SqQueue &Q, ElemType &x){    
    // 如果队列为空直接返回    
    if(Q.rear == Q.front)  
        return false;     
    x = Q.data[Q.front];  
    Q.front = (Q.front+1)%MaxSize;
    return true;
}
 

  • 循环队列不能直接使用Q.rear == Q.front作为判空的条件，因为当队列已满时也符合该条件，会与判空发生冲突！
 

解决方法一：牺牲一个单元来区分队空和队满，即将(Q.rear+1)%MaxSize == Q.front作为判断队列是否已满的条件。（主流方法）
解决方法二：设置 size 变量记录队列长度。
 

#define MaxSize 10; 
 
typedef struct{   
    ElemType data[MaxSize]; 
    int front, rear;    
    int size;
}SqQueue;
 
// 初始化队列
void InitQueue(SqQueue &Q){ 
    Q.rear = Q.front = 0;   
    Q.size = 0;
}
 
// 判断队列是否为空
bool QueueEmpty(SqQueue 0){     
    if(Q.size == 0)      
        return true;   
    else       
        return false;
}
 
// 新元素入队
bool EnQueue(SqQueue &Q, ElemType x){ 
    if(Q.size == MaxSize)    
        return false;
    Q.size++; 
    Q.data[Q.rear] = x; 
    Q.rear = (Q.rear+1)%MaxSize;  
    return true;
}
 
// 出队
bool DeQueue(SqQueue &Q, ElemType &x){   
    if(Q.size == 0)        
        return false;
    Q.size--;
    x = Q.data[Q.front]; 
    Q.front = (Q.front+1)%MaxSize; 
    return true;
}
 

解决方法三：设置 tag 变量记录队列最近的操作。（tag=0：最近进行的是删除操作；tag=1 ：最近进行的是插入操作）
 

#define MaxSize 10;   
 
typedef struct{    
    ElemType data[MaxSize]; 
    int front, rear;        
    int tag;
}SqQueue;
 
// 初始化队列
void InitQueue(SqQueue &Q){    
    Q.rear = Q.front = 0;   
    Q.tag = 0;
}
 
// 判断队列是否为空，只有tag==0即初始化或者出队后才可能为空
bool QueueEmpty(SqQueue 0){  
    if(Q.front == Q.rear && Q.tag == 0)    
        return true;   
    else       
        return false;
}
 
// 新元素入队 判断队列是否满，只有tag==1即入队后才可能满
bool EnQueue(SqQueue &Q, ElemType x){
    if(Q.rear == Q.front && tag == 1)     
        return false;     
    Q.data[Q.rear] = x; 
    Q.rear = (Q.rear+1)%MaxSize;  
    Q.tag = 1;  
    return true;
}
 
// 出队
bool DeQueue(SqQueue &Q, ElemType &x){
    if(Q.rear == Q.front && tag == 0)  
        return false;   
    x = Q.data[Q.front];
    Q.front = (Q.front+1)%MaxSize; 
    Q.tag = 0;     
    return true;
}
 

【获得队头元素】
 

// 获取队头元素并存入x
bool GetHead(SqQueue &Q, ElemType &x){
    if(Q.rear == Q.front)      
        return false;
    x = Q.data[Q.front];  
    return true;
}
 

队列的链式存储实现
 

【链队列的定义】
 

// 链式队列结点
typedef struct LinkNode{  
    ElemType data;    
    struct LinkNode *next;
}
 
// 链式队列
typedef struct{       
    // 头指针和尾指针  
    LinkNode *front, *rear;
}LinkQueue;
 

【 链队列的初始化（带头结点）】
 

typedef struct LinkNode{    
    ElemType data;     
    struct LinkNode *next;
}LinkNode;
 
typedef struct{    
    LinkNode *front, *rear;
}LinkQueue;
 
// 初始化队列
void InitQueue(LinkQueue &Q){   
    // 初始化时，front、rear都指向头结点 
    Q.front = Q.rear = (LinkNode *)malloc(sizeof(LinkNode));  
    Q.front -> next = NULL;
}
 
// 判断队列是否为空
bool IsEmpty(LinkQueue Q){ 
    if(Q.front == Q.rear)     
        return true;      
    else         
        return false;
}
 

【入队出队（带头结点）】
 

// 新元素入队
void EnQueue(LinkQueue &Q, ElemType x){ // 不存在满的情况
    LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode)); 
    s->data = x;  
    s->next = NULL; 
    Q.rear->next = s;  
    Q.rear = s;
}
 
// 队头元素出队
bool DeQueue(LinkQueue &Q, ElemType &x){   
    if(Q.front == Q.rear)  // 判空       
        return false;    
    LinkNode *p = Q.front->next; 
    x = p->data;   
    Q.front->next = p->next; 
    // 如果p是最后一个结点，此时Q.rear已经要被删除了，则将队尾指针也指向队首指针  
    if(Q.rear == p)          
        Q.rear = Q.front;   
    free(p);
    p = NULL;    
    return true;
}
 

【不带头结点的链队列操作】
 

typedef struct LinkNode{   
    ElemType data;  
    struct LinkNode *next;
}LinkNode;
 
typedef struct{   
    LinkNode *front, *rear;
}LinkQueue;
 
// 初始化队列
void InitQueue(LinkQueue &Q){ 
    // 不带头结点的链队列初始化，头指针和尾指针都指向NULL
    Q.front = NULL;   
    Q.rear = NULL;
}
 
// 判断队列是否为空
bool IsEmpty(LinkQueue Q){ 
    if(Q.front == NULL)   
        return true;      
    else             
        return false;
}
 
// 新元素入队
void EnQueue(LinkQueue &Q, ElemType x){ 
    LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));  
    s->data = x;   
    s->next = NULL; 
    // 第一个元素入队时需要特别处理   
    if(Q.front == NULL){
        Q.front = s;    
        Q.rear = s; 
    }else{
        Q.rear->next = s;
        Q.rear = s;
    }
}
 
//队头元素出队
bool DeQueue(LinkQueue &Q, ElemType &x){
    if(Q.front == NULL)
        return false;
    LinkNode *s = Q.front;
    x = s->data;
    if(Q.front == Q.rear){
        Q.front = Q.rear = NULL;
    }else{
        Q.front = Q.front->next;
    }
    free(s);
    return true;
}
 

双端队列
 

双端队列定义 
 

  • 双端队列是允许从两端插入、两端删除的线性表。
  • 如果只使用其中一端的插入、删除操作，则等同于栈。
  • 输入受限的双端队列：允许一端插入，两端删除的线性表。
  • 输出受限的双端队列：允许两端插入，一端删除的线性表。
 

 

双端队列考点：判断输出序列的合法化
 

  • 例：数据元素输入序列为 1，2，3，4，判断 4! = 24 个输出序列的合法性
            输入受限的双端队列：只有 4213 和 4231 不合法
            输出受限的双端队列：只有 4132 和 4231 不合法

                

        

        

            

            

            

              

                本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1213835.html
              

              如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！
            

            
            

              
            

          


            
相关文章

          
            
                  

                    

                      

                        

                          
                            数据结构—LinkedList与链表
                        

                      

                      

                        

                          数据结构—LinkedList与链表
                        

                        

                          目录 
一、链表 
1. 链表的概念及结构 
1. 单向或者双向 
2. 带头或者不带头 
3. 循环或者非循环 
二.LinkedList的使用 1.LinkedList概念及结构 
2. LinkedList的构造 
3. LinkedList的方法 
三. ArrayList和LinkedList的区别 一、链表  
1. 链表的概念及结构  链表是一种 物理…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            Postman实现接口的文件上传
                        

                      

                      

                        

                          Postman实现接口的文件上传
                        

                        

                          近期在复习Postman的基础知识，在小破站上跟着百里老师系统复习了一遍，也做了一些笔记，希望可以给大家一点点启发。 接口的文件上传，与其他接口的传参差不多，只要点击form-data，选择要上传的文件即可。 实际…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            Java第十九章
                        

                      

                      

                        

                          Java第十九章
                        

                        

                          一.绘制图形 
Java 可以分别使用 Graphics类和Graphics2D 类绘制图形，Graphics 类使用不同的方法实现不同图形的绘制。例如，drawLine()方法可以绘制直线，drawRect()方法用于绘制矩形，drawOval()方法用于绘制椭圆形等。 例1. 例2. …
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            物联网项目：充电桩项目实战~
                        

                      

                      

                        

                          物联网项目：充电桩项目实战~
                        

                        

                          你好，我是田哥 最近除了忙于面试辅导、模拟面试以外，还在搞一件大事：充电桩项目。 分布式微服务项目实战：充电桩项目 充电桩项目肯定是和物联网相关的，聊到物联网又不得不聊的是MQTT协议。 什么是MQTT MQTT&#xff0c…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            数据结构前言（空间复杂度）
                        

                      

                      

                        

                          数据结构前言（空间复杂度）
                        

                        

                          1.空间复杂度 
空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 。 
空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。 空间复杂度计算规则基本跟实践复杂…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            解决Github上的README无法显示图片
                        

                      

                      

                        

                          解决Github上的README无法显示图片
                        

                        

                          首先感谢博主的思路：思路 
最近写了点东西提交到git 发现本地能查看md里的图片用的相对路径，提交到github就看不见，并且发现不只是我自己的仓库看不见，其他人的我也看不见。那就有问题了  
解决：正常使用相对路径&…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            C#中.NET Framework4.8 Windows窗体应用通过EF访问新建数据库
                        

                      

                      

                        

                          C#中.NET Framework4.8 Windows窗体应用通过EF访问新建数据库
                        

                        

                          目录 
一、 操作步骤 
二、编写EF模型和数据库上下文 
三、 移植（Migrations）数据库 
四、编写应用程序 
五、生成效果 前文已经说过.NET Framework4.8 控制台应用通过EF访问已经建立的和新建的数据库。  本文想说的是，.NET Framework4.8 Win…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            黑豹程序员-SpringCloudAlibaba聚合工程打包和运行
                        

                      

                      

                        

                          黑豹程序员-SpringCloudAlibaba聚合工程打包和运行
                        

                        

                          文章目录 1、SpringCloudAlibaba项目结构2、打包配置3、打包4、运行 1、SpringCloudAlibaba项目结构 2、打包配置 3、打包 4、运行 
java -jar rms-parent.jar
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            解决：java: 错误: 不支持发行版本 5 最有效方法
                        

                      

                      

                        

                          解决：java: 错误: 不支持发行版本 5 最有效方法
                        

                        

                          报错信息如图&#xff1a; 直接上终极方法&#xff1a; 修改配置文件 如图找到settings.xml文件  在标签中间插入如下代码&#xff08;jdk更改为自己电脑上的版本&#xff09; <profile><id>development</id><activation><jdk>11</jdk><…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            SQL练习---619.出现一次的最大数字
                        

                      

                      

                        

                          SQL练习---619.出现一次的最大数字
                        

                        

                          题目 分析 
首先确定表的来源只有一个表数字表&#xff0c;再者判断他是不是单一数字&#xff0c;&#xff08;想到的是直接按数字分组&#xff0c;通过count函数来判断是否为单一数子&#xff09;&#xff0c;然后求最大值。 
题解 
select Max(num) as num from MyNumbers
wh…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            EMNLP 2023 | DeepMind提出大模型In-Context Learning的可解释理论框架
                        

                      

                      

                        

                          EMNLP 2023 | DeepMind提出大模型In-Context Learning的可解释理论框架
                        

                        

                          论文题目&#xff1a;In-Context Learning Creates Task Vectors 论文链接&#xff1a;https://arxiv.org/abs/2310.15916 01. 引言 此外&#xff0c;作者也提到本文的方法与软提示&#xff08;soft-prompt&#xff09;[1]方法类似&#xff0c;soft-prompt也是通过调整大模型内…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            C语言查看main函数的参数
                        

                      

                      

                        

                          C语言查看main函数的参数
                        

                        

                          这里写自定义目录标题 argc 代表参数的个数argv 代表参数的具体值&#xff0c;其中argv[0]代表的是可执行文件的名字&#xff0c;参考上图
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            [工业自动化-22]：西门子S7-15xxx编程 - 软件编程 - 如何PLC建立用户界面: SIMATIC 面板式HMI 或工控机PC HMI
                        

                      

                      

                        

                          [工业自动化-22]：西门子S7-15xxx编程 - 软件编程 - 如何PLC建立用户界面: SIMATIC 面板式HMI 或工控机PC HMI
                        

                        

                          目录 
前言&#xff1a; 
一、PLC&#xff08;可编程逻辑控制器&#xff09;的用户界面支持方式 
1.1 概述 
1.2 西门子&#xff08;Siemens&#xff09;的人机界面&#xff08;HMI&#xff09;支持多种类型 
1.3 PC HMI VS SIMATIC HMI 
二、PC—HMI—PLC连接架构的实现 
三、…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            百度曹海涛：生成式AI正从“探索能力边界”向“推动应用落地”过渡
                        

                      

                      

                        

                          百度曹海涛：生成式AI正从“探索能力边界”向“推动应用落地”过渡
                        

                        

                          11月9日&#xff0c;以“星云棋布&#xff0c;步步为‘赢’”为主题的2023 IDC中国生态峰会在北京举办。会上&#xff0c;IDC中国区总裁霍锦洁女士的发表致辞。同时&#xff0c;IDC生态伙伴和行业领袖从多重维度分析了AI技术应用的发展&#xff0c;以及对于整体IT生态所产生的影…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            虹科方案 | 从概念到生产的自动驾驶软件在环（SiL）测试解决方案
                        

                      

                      

                        

                          虹科方案 | 从概念到生产的自动驾驶软件在环（SiL）测试解决方案
                        

                        

                          来源&#xff1a;雅名特自动驾驶 虹科方案 | 从概念到生产的自动驾驶软件在环&#xff08;SiL&#xff09;测试解决方案 自动驾驶软件在环&#xff08;SiL&#xff09;测试解决方案 
自动驾驶软件在环&#xff08;SiL&#xff09;测试解决方案能够研究和验证高历程实验和恶劣驾…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            PCA降维Python demo
                        

                      

                      

                        

                          PCA降维Python demo
                        

                        

                          读这篇15年CVPR的文章&#x1f923;&#x1f923;&#x1f923;&#x1f923;&#x1f923; 
inproceedings{liu2015sparse,title{Sparse convolutional neural networks},author{Liu, Baoyuan and Wang, Min and Foroosh, Hassan and Tappen, Marshall and Pensky, Marianna},…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            Android 框架
                        

                      

                      

                        

                          Android 框架
                        

                        

                          MVC: 
MVP 
MVVM Model 数据以及业务数据 
View 视图 
Control 控制器 simple code MVP OnFinishInflate ViewGroup 加载完成 
MVC 优化 Struts 
MVC- MVP 
MVC-单次调用逻辑把 
MVP / 把C拆分出来 MVVM 2017Google推出ViewModel DataBind 
MVVM是一种框架规则,双向绑定 
Model…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            91.移动零（力扣）
                        

                      

                      

                        

                          91.移动零（力扣）
                        

                        

                          问题描述 代码解决以及思想  
class Solution {
public:void moveZeroes(vector<int>& nums) {int left  0;   // 左指针&#xff0c;用于指向当前非零元素应该放置的位置int right  0;  // 右指针&#xff0c;用于遍历数组int len  nums.size();  // 数组长度while …
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            kubectl get nodes报错：The connection to the server localhost:8080
                        

                      

                      

                        

                          kubectl get nodes报错：The connection to the server localhost:8080
                        

                        

                          报错描述kubectl get nodes命令无法执行 
在K8S-master初始化后&#xff0c;worker-node节点加入K8S集群后 
kubeadm join 192.168.31.150:6443 --token 2n0t62.gvuu8x3zui9o8xnc \--discovery-token-ca-cert-hash sha256:d294c082cc7e0d5f620fb10e527a8a7cb4cb6ccd8dc45ffaf2c…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
                  

                    

                      

                        

                          
                            TikTok与心灵成长：娱乐与启发并重
                        

                      

                      

                        

                          TikTok与心灵成长：娱乐与启发并重
                        

                        

                          社交媒体已成为我们生活的一部分&#xff0c;其中TikTok以其短视频内容和创新性而闻名。然而&#xff0c;TikTok不仅仅是一个娱乐平台&#xff0c;它还具有潜力成为心灵成长的有力工具。本文将探讨TikTok如何在娱乐与启发之间取得平衡&#xff0c;以促进心灵成长和积极影响。 娱…
                        

                        

                          阅读更多...
                        

                      

                    

                  

                  
       
      
        

        

          

            



                
                
                

            

          

          

            



              
推荐文章

              
            

          


          

            


                
                
                
            

          

          

            

              
最新文章

              
            

          

          

            

            
            
            
            

          

        

      

    

    

      

        

                    Copyright @ 2022~2023