文章目录
- 一、普通函数 与 函数模板 的调用规则 - 类型自动转换
- 1、函数模板和重载函数
- 2、类型自动转换
- 3、代码示例 - 类型自动转换
- 二、普通函数 与 函数模板 的调用规则 - 类型自动转换 + 显式指定泛型类型
- 1、类型自动转换 + 显式指定泛型类型
- 2、代码示例 - 类型自动转换 + 显式指定泛型类型
一、普通函数 与 函数模板 的调用规则 - 类型自动转换
1、函数模板和重载函数
定义了 函数模板 , 该 函数模板 可以接收 任意类型的参数 T , 但是要求这两个参数类型 T 和 返回值类型 T 必须是相同的 ;
// 使用 template 关键字 声明函数模板
// 告诉 C++ 编译器 开始使用 泛型编程
// 定义的 T 是泛型类型
// 声明了多个泛型, 可以只使用其中的部分类型
// 使用函数模板时 , 显式类型调用 必须 显式指定所有 泛型类型 的实际类型
template <typename T>
T add(T a, T b) {
cout << "调用函数模板 T add(T a, T b)" << endl;
return a + b;
}
此外还定义了 函数模板 的 重载函数 , 该重载函数 接收两个 int 类型的参数 , 同时返回 int 类型的返回值 ;
// 函数模板的 重载函数
// 重载是发生在 同一个作用域中
// 重写是发生在 父类 与 子类 之间
// C++ 编译器优先 调用 符合要求的 普通函数
// 如果普通函数不符合要求 , 则考虑调用 函数模板
int add(int a, int b) {
cout << "调用普通函数 int add(int a, int b)" << endl;
return a + b;
}
2、类型自动转换
当 函数模板 有 重载的 普通函数时 , 普通函数 调用 优先级 高于 函数模板 ;
函数模板 会进行 严格类型匹配 , 不会进行 类型转换 ;
普通函数 如果 遇到 参数不匹配的情况 , 会将 函数参数 进行类型自动转换 ;
函数模板 与 普通函数 在 类型自动转换 方面调用规则如下 :
- 首先 , 如果 符合 普通函数类型参数要求 , 优先调用普通函数 ;
- 然后 , 如果 没有 符合要求的 普通函数 , 则查看 模板函数 能否匹配 ;
- 最后 , 如果 模板函数 仍不能匹配 , 则查看 普通函数 类型转换能否匹配 ;
3、代码示例 - 类型自动转换
代码示例 :
#include "iostream"
using namespace std;
// 使用 template 关键字 声明函数模板
// 告诉 C++ 编译器 开始使用 泛型编程
// 定义的 T 是泛型类型
// 声明了多个泛型, 可以只使用其中的部分类型
// 使用函数模板时 , 显式类型调用 必须 显式指定所有 泛型类型 的实际类型
template <typename T>
T add(T a, T b) {
cout << "调用函数模板 T add(T a, T b)" << endl;
return a + b;
}
// 函数模板的 重载函数
// 重载是发生在 同一个作用域中
// 重写是发生在 父类 与 子类 之间
// C++ 编译器优先 调用 符合要求的 普通函数
// 如果普通函数不符合要求 , 则考虑调用 函数模板
int add(int a, int b) {
cout << "调用普通函数 int add(int a, int b)" << endl;
return a + b;
}
// 普通函数 调用 优先级 高于 函数模板
// 函数模板 会进行 严格类型匹配 , 不会进行 类型转换 ;
//
// 如果 符合 普通函数类型参数要求 , 优先调用普通函数 ;
// 如果 没有 符合要求的 普通函数 , 则查看 模板函数 能否匹配 ;
// 如果 模板函数 仍不能匹配 , 则查看 普通函数 类型转换能否匹配 ;
int main() {
int a = 10, b = 20;
char x = 'A', y = 'B';
// 调用普通函数
// 如果符合普通函数要求 优先调用普通函数
int c = add(a, b);
cout << "c = " << c << endl;
// 调用 函数模板
// 普通函数类型不匹配, 查看 模板函数 能否匹配
// 模板函数可以匹配
int d = add(x, y);
cout << "d = " << d << endl;
// 调用 普通函数
// 普通函数类型不匹配, 查看 模板函数 能否匹配
// 模板函数不可以匹配 , 继续查看 普通函数 类型自动转换
// x 可以转为 int 类型 , 这样就可以符合普通函数参数要求
int e = add(a, x);
cout << "e = " << e << endl;
// 控制台暂停 , 按任意键继续向后执行
system("pause");
return 0;
}
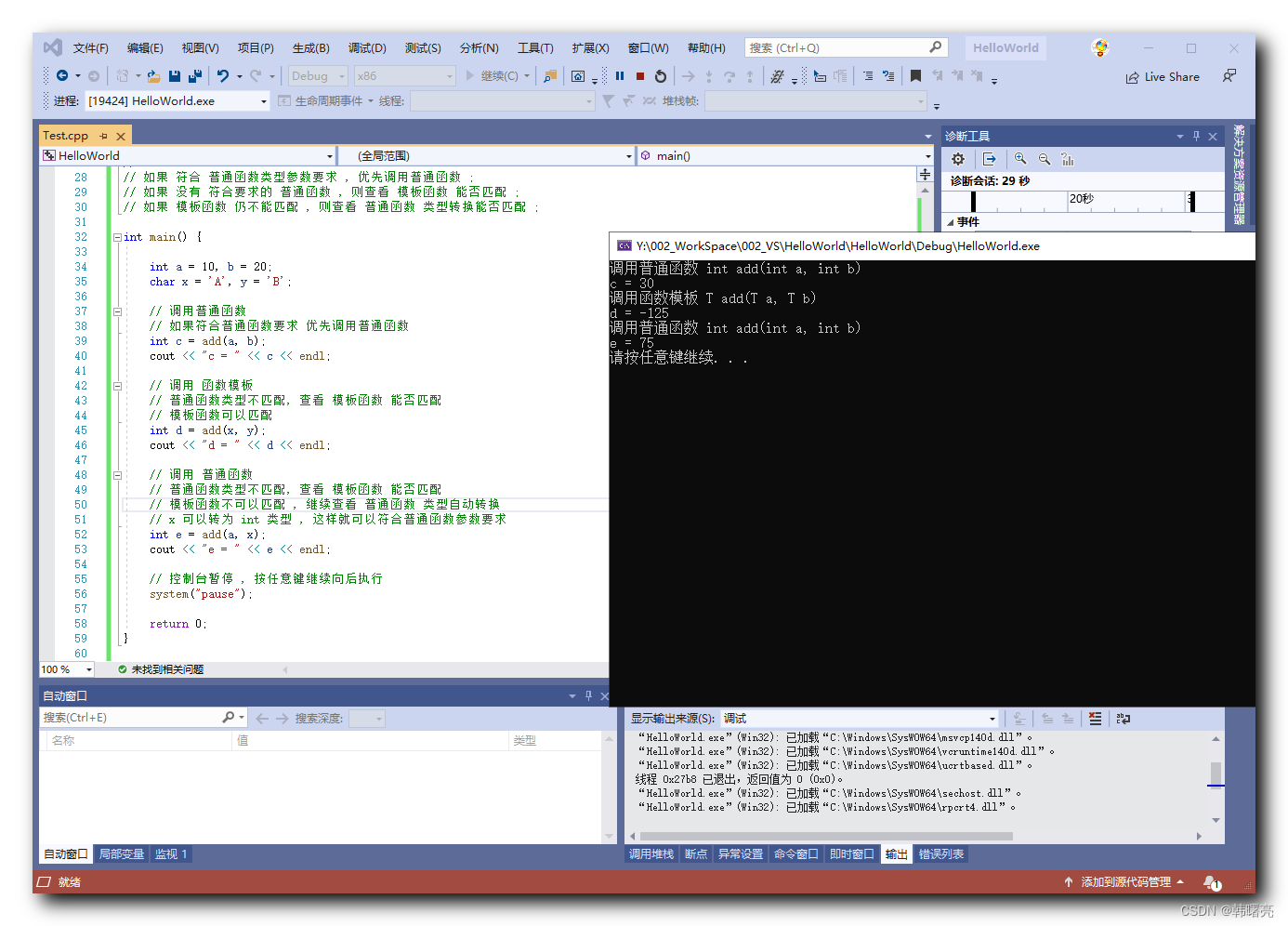
执行结果 :
调用普通函数 int add(int a, int b)
c = 30
调用函数模板 T add(T a, T b)
d = -125
调用普通函数 int add(int a, int b)
e = 75
请按任意键继续. . .
二、普通函数 与 函数模板 的调用规则 - 类型自动转换 + 显式指定泛型类型
1、类型自动转换 + 显式指定泛型类型
在上面示例的前提下 , 如果 传入参数 类型分别是 int 和 char , 并且强行指定 泛型类型 , 这样必须使用函数模板 , 此时 函数模板 也可以进行 类型自动转换 ;
int a = 10, b = 20;
char x = 'A', y = 'B';
// 调用 函数模板
// 函数模板 显式类型调用 , 强行使用 函数模板
int k = add<int>(a, x);
cout << "k = " << k << endl;
2、代码示例 - 类型自动转换 + 显式指定泛型类型
代码示例 :
#include "iostream"
using namespace std;
// 使用 template 关键字 声明函数模板
// 告诉 C++ 编译器 开始使用 泛型编程
// 定义的 T 是泛型类型
// 声明了多个泛型, 可以只使用其中的部分类型
// 使用函数模板时 , 显式类型调用 必须 显式指定所有 泛型类型 的实际类型
template <typename T>
T add(T a, T b) {
cout << "调用函数模板 T add(T a, T b)" << endl;
return a + b;
}
// 函数模板的 重载函数
// 重载是发生在 同一个作用域中
// 重写是发生在 父类 与 子类 之间
// C++ 编译器优先 调用 符合要求的 普通函数
// 如果普通函数不符合要求 , 则考虑调用 函数模板
int add(int a, int b) {
cout << "调用普通函数 int add(int a, int b)" << endl;
return a + b;
}
// 普通函数 调用 优先级 高于 函数模板
// 函数模板 会进行 严格类型匹配 , 不会进行 类型转换 ;
//
// 如果 符合 普通函数类型参数要求 , 优先调用普通函数 ;
// 如果 没有 符合要求的 普通函数 , 则查看 模板函数 能否匹配 ;
// 如果 模板函数 仍不能匹配 , 则查看 普通函数 类型转换能否匹配 ;
int main() {
int a = 10, b = 20;
char x = 'A', y = 'B';
// 调用普通函数
// 如果符合普通函数要求 优先调用普通函数
int c = add(a, b);
cout << "c = " << c << endl;
// 调用 函数模板
// 普通函数类型不匹配, 查看 模板函数 能否匹配
// 模板函数可以匹配
int d = add(x, y);
cout << "d = " << d << endl;
// 调用 普通函数
// 普通函数类型不匹配, 查看 模板函数 能否匹配
// 模板函数不可以匹配 , 继续查看 普通函数 类型自动转换
// x 可以转为 int 类型 , 这样就可以符合普通函数参数要求
int e = add(a, x);
cout << "e = " << e << endl;
// 调用 函数模板
// 函数模板 显式类型调用 , 强行使用 函数模板
int k = add<int>(a, x);
cout << "k = " << k << endl;
// 控制台暂停 , 按任意键继续向后执行
system("pause");
return 0;
}
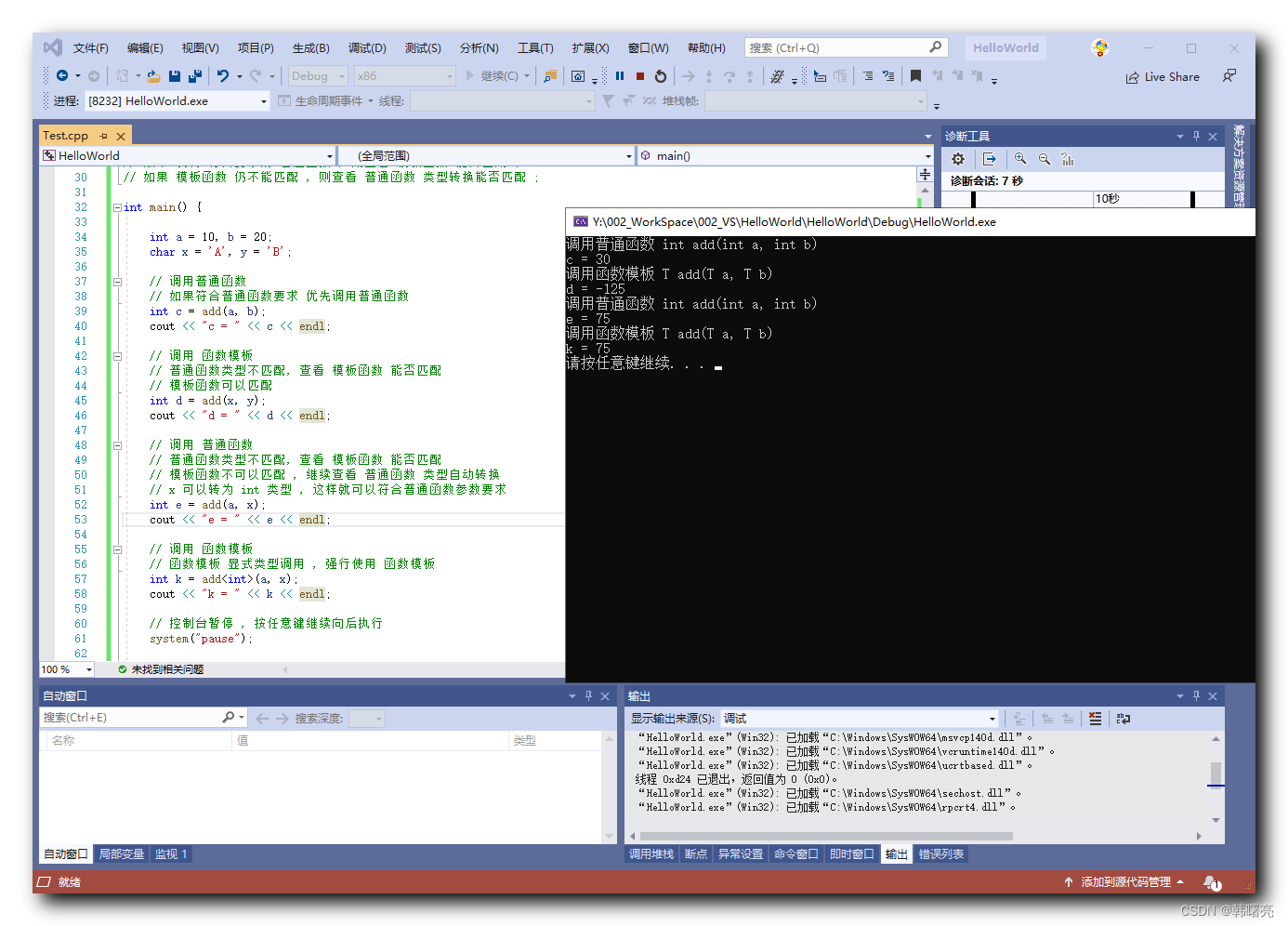
执行结果 :
调用普通函数 int add(int a, int b)
c = 30
调用函数模板 T add(T a, T b)
d = -125
调用普通函数 int add(int a, int b)
e = 75
调用函数模板 T add(T a, T b)
k = 75
请按任意键继续. . .





![[PyTorch][chapter 63][强化学习-QLearning]](https://img-blog.csdnimg.cn/933bd586568f494fa86a22caa39a6652.png)