1.下载qt5.15.11源码

https://download.qt.io/official_releases/qt/5.15/5.15.11/single/qt-everywhere-opensource-src-5.15.11.zip

2.解码源码到桌面

 3.安装cmake ,python ,perl, Visual Studio 2019

Strawberry Perl for Windows

Win flex-bison download | SourceForge.net 

 Download gperf-3.0.1.exe (GnuWin) (sourceforge.net)

CMake - Upgrade Your Software Build System

Visual Studio: 面向软件开发人员和 Teams 的 IDE 和代码编辑器 (microsoft.com) 

 4.进入解压后的源码目录，

配置:   configure -release -nomake examples -nomake tests -skip qtwebengine -opensource

配置成功

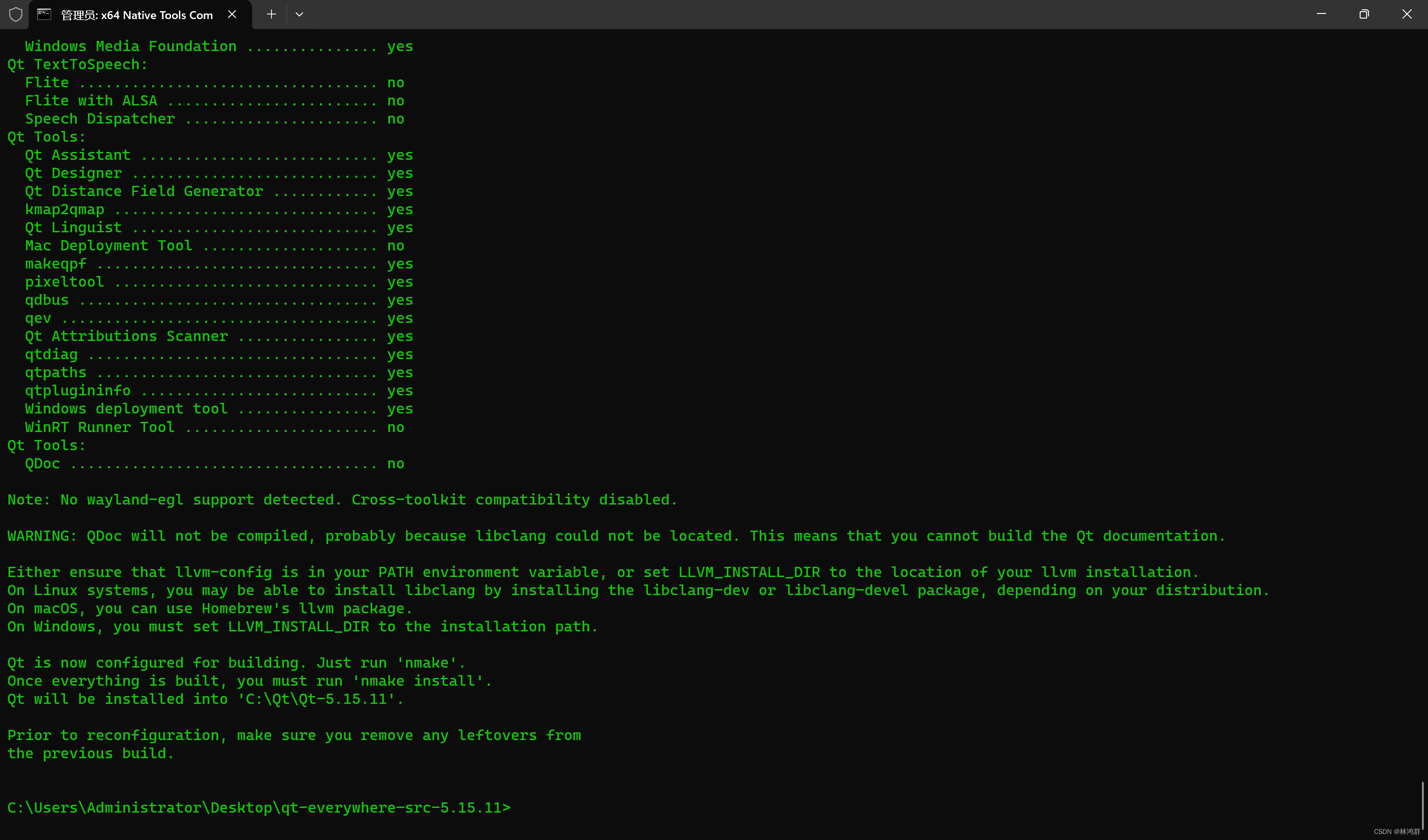 编译： nmake 

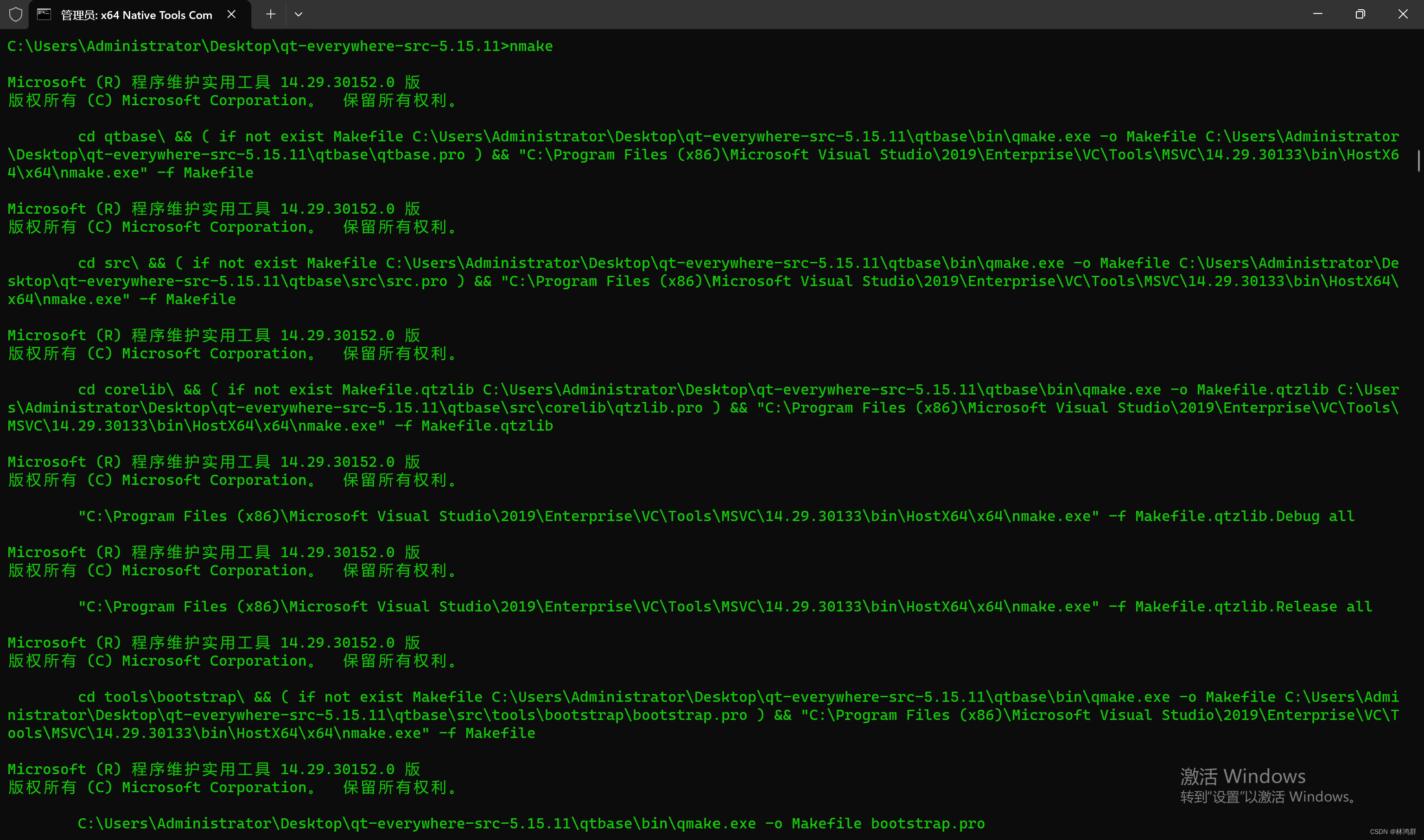
安装:  nmake install

安装成功：