机器学习的线性回归与非线性回归

news2024/11/13 9:34:08

一元线性回归

回归分析用来建立方程模拟两个或者多个变量之间如何关联

一元线性回归包括一个自变量和一个因变量

如果包含两个以上的自变量，则称为多元线性回归

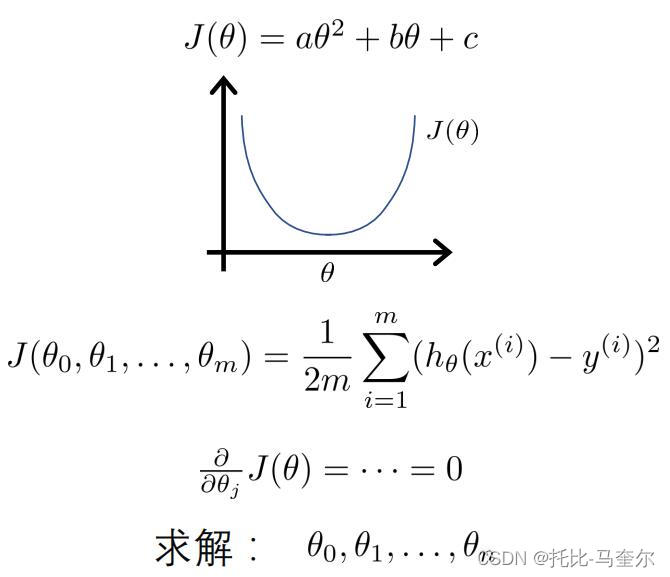
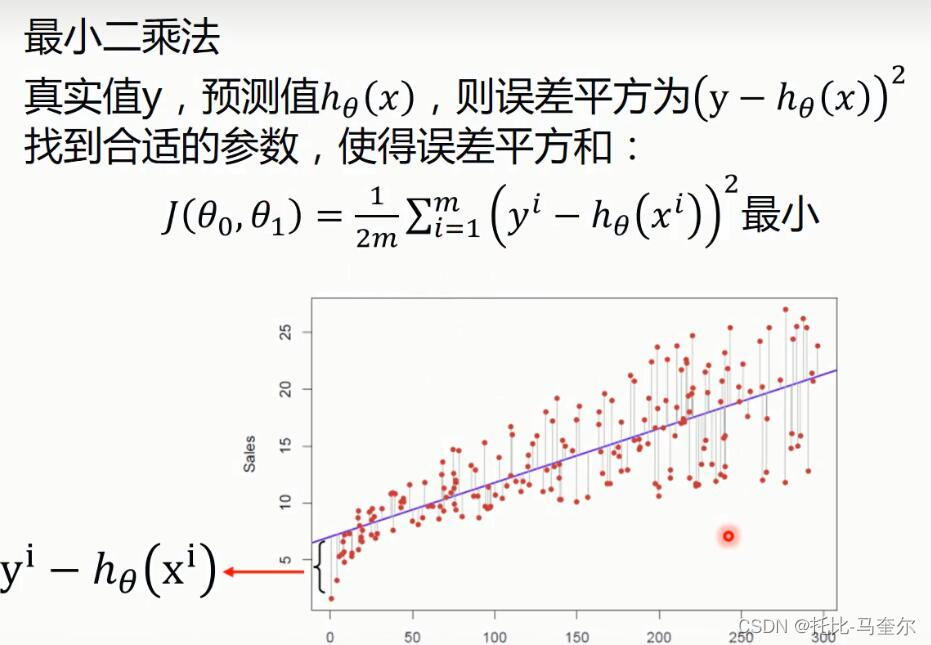
代价函数（损失函数）

损失函数的最终目的是为了使得误差平方和最小

用梯度下降法求解线性回归

 训练模型过程中不断重复这个语句

 学习率的值不能太小，也不能太大

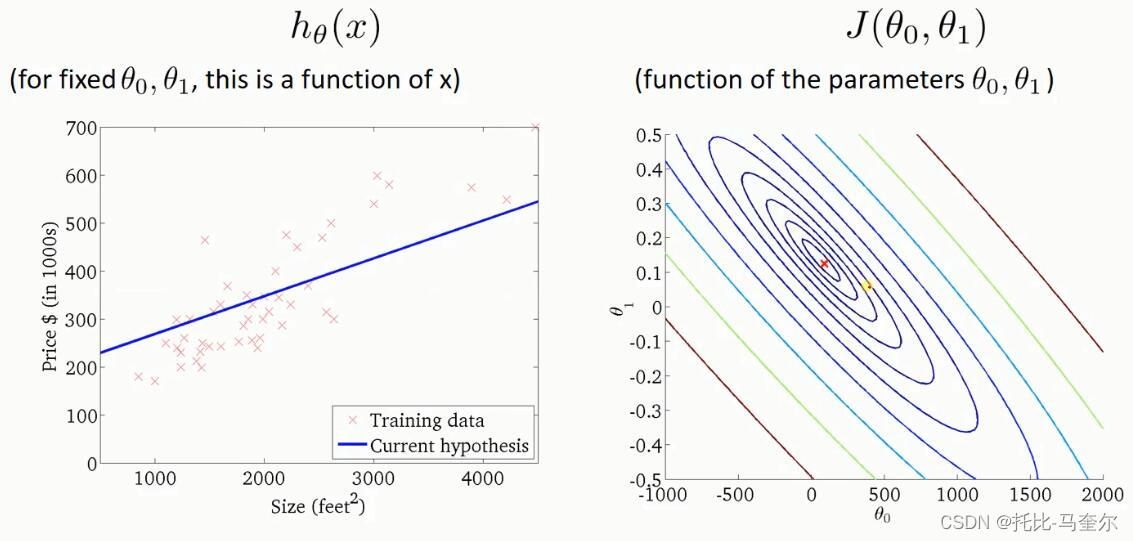
 右边同一个颜色的线上任意一点，最终取得的损失函数的值是相等的

最中间的线上取得的损失函数值是最小的

 梯度下降法 一元线性回归

import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt("data.csv",delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
# plt.scatter()函数用于创建一个散点图
plt.scatter(x_data,y_data)
plt.show()

 最小二乘法

# 最小二乘法
def compute_error(b, k, x_data, y_data):
    # 代价函数的初始值
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
    return totalError / float(len(x_data)) / 2.0

 梯度下降法

def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
    # 计算总数据量
    m = float(len(x_data))
    # 循环epochs次
    for i in range(epochs):
        b_grad = 0
        k_grad = 0
        # 计算梯度的总和再求平均
        for j in range(0, len(x_data)):
            b_grad += (1/m) * (((k*x_data[j]) + b) - y_data[j])
            k_grad += (1/m) * x_data[j] * (((k*x_data[j]) + b) - y_data[j])
        # 更新b和k
        b = b - (lr * b_grad)
        k = k - (lr * k_grad)

    return b,k

输出和图象

print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
print("Running……")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
print("After{0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))

# 画图
plt.plot(x_data, y_data, 'b.') # 用蓝色的点画出来
plt.plot(x_data, k*x_data + b, 'r')
plt.show()

 sklearn-一元线性回归

from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt("data.csv",delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()
print(x_data.shape)

画出散点图；最后输出值为(100,) 

 创建并拟合模型

# 从 data 中选择所有行和第一列，然后增加一个维度，形成一个二维数组
x_data = data[:,0,np.newaxis]
y_data = data[:,1,np.newaxis]
# 创建并拟合模型
model = LinearRegression()
model.fit(x_data, y_data)

 LinearRegression模型通常需要输入二维数组形式的数据来进行拟合。这是因为线性回归模型通常表示为矩阵形式。

np.newaxis增加一个维度是为了将一维数组转换为二维数组，使得数据可以以矩阵的形式输入到模型中。

x_data 和 y_data 分别表示输入数据和目标数据。通过增加一个维度，它们被转换为二维数组，可以作为线性回归模型的输入。这样，模型就可以通过拟合这些数据来学习输入和输出之间的关系，并预测新的数据

 画图

# 画图
plt.plot(x_data, y_data, 'b.') # 用蓝色的点画出来
plt.plot(x_data, model.predict(x_data), 'r')
plt.show()

 多元线性回归

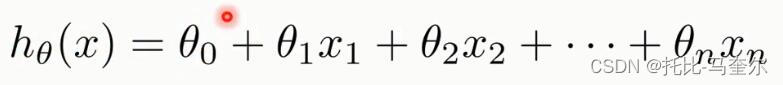
 梯度下降法-多元线性回归

import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 载入数据
# 使用r前缀表示一个字符串是原始字符串，即不会对其中的转义字符进行解析
data = np.genfromtxt(r"Delivery.csv",delimiter=",")
print(data)

切分数据

# 切分数据
# 取到最后一个列，但不包括最后一个列
x_data = data[:,:-1]
y_data = data[:,-1]
print(x_data)
print(y_data)

 最小二乘法

# 最小二乘法
def compute_error(theta0, theta1, theta2, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (theta1 * x_data[i,0] + theta2 * x_data[i,1] + theta0)) ** 2
    return totalError / float(len(x_data)) / 2.0

 梯度下降法

def gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs):
    # 计算总数据量
    m = float(len(x_data))
    # 循环epochs次
    for i in range(epochs):
        theta0_grad = 0
        theta1_grad = 0
        theta2_grad = 0
        # 计算梯度的总和再求平均
        for j in range(0, len(x_data)):
            theta0_grad += (1/m) * ((theta1 *x_data[j,0] + theta2*x_data[j,1] + theta0)- y_data[j])
            theta1_grad += (1/m) * x_data[j,0] * ((theta1 *x_data[j,0] + theta2*x_data[j,1] + theta0)- y_data[j])
            theta2_grad += (1/m) * x_data[j,1] * ((theta1 *x_data[j,0] + theta2*x_data[j,1] + theta0)- y_data[j])
        # 更新b和k
        theta0 = theta0 - (lr*theta0_grad)
        theta1 = theta1 - (lr*theta1_grad)
        theta2 = theta2 - (lr*theta2_grad)
    return theta0, theta1, theta2

 输出

print("Starting theta0 = {0}, theta1 = {1}, theta2 = {2}, error = {3}".format(theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)))
print("Running...")
theta0, theta1, theta2 = gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs)
print("After {0} iterations theta0 = {1}, theta1 = {2}, theta2 = {3}, error = {4}".format(epochs, theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)))

Starting theta0 = 0.006971416196678632, theta1 = 0.08021042690771771, theta2 = 0.07611036240566814, error = 0.3865635716109059

Running...

After 1000 iterations theta0 = 0.012105936219977274, theta1 = 0.07783523865497854, theta2 = 0.14266718993616928, error = 0.34191327566030316

 画3D图

# 画3D图
# 在图形上添加一个子图，其中'111'表示这是一个占据整个图形的子图
#（即，它覆盖了从左上角开始的第一行、# 第一列和第一页的网格的单元格）。
# projection = '3d'表示我们想要创建一个3D的子图
ax = plt.figure().add_subplot(111, projection = '3d')
ax.scatter(x_data[:,0],x_data[:,1],y_data, c = 'r', marker = 'o', s = 100)
# 格式是圆点，每个点的大小为100
x0 = x_data[:,0]
x1 = x_data[:,1]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = theta0 + x0*theta1 + x1*theta2
#画3D图
#这个函数能创建三维曲面图
ax.plot_surface(x0, x1, z)
# 设置坐标轴
ax.set_xlabel('Miles')
ax.set_ylabel('Num of Deliveries')
ax.set_zlabel('Time')

# 显示图象
plt.show()

sklearn-多元线性回归

import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 读入数据
data = np.genfromtxt(r"Delivery.csv",delimiter=",")
print(data)

 切分数据

# 切分数据
# 取到最后一个列，但不包括最后一个列
x_data = data[:,:-1]
y_data = data[:,-1]
print(x_data)
print(y_data)

创建模型

# 创建模型
model = linear_model.LinearRegression()
model.fit(x_data, y_data)

 输出

# 系数
print("coefficients:",model.coef_)

# 截距
print("intercept:",model.intercept_)

画3D图

# 画3D图
ax = plt.figure().add_subplot(111, projection = '3d')
ax.scatter(x_data[:,0],x_data[:,1],y_data, c = 'r', marker = 'o', s = 100)
# 格式是圆点，大小为100
x0 = x_data[:,0]
x1 = x_data[:,1]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = model.intercept_ + x0*model.coef_[0] + x1*model.coef_[1]
#画3D图
ax.plot_surface(x0, x1, z)
# 设置坐标轴
ax.set_xlabel('Miles')
ax.set_ylabel('Num of Deliveries')
ax.set_zlabel('Time')

# 显示图象
plt.show()

多项式回归

sklearn-多项式回归 

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
# 载入数据
data = np.genfromtxt("job.csv", delimiter=",")
# 从 data 数组的第二行开始，选择所有行的第一列数据
x_data = data[1:,1]
y_data = data[1:,2]
print(x_data)
plt.scatter(x_data, y_data)
plt.show()

 创建并拟合模型

x_data = data[1:,1,np.newaxis]
y_data = data[1:,2,np.newaxis]
# 创建并拟合模型
model = LinearRegression()
model.fit(x_data, y_data)

 线性图

# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, model.predict(x_data), 'r')
plt.show()

 定义多项式回归

# 定义多项式回归，degree的值可以调节多项式的特征
# 当 degree=1 时，PolynomialFeatures 实际上不会生成新的特征，
# 而是会生成一个包含常数项 1 的特征，生成的第一列都是 1.0

# degree参数代表多项式的次数
# fit_transform()可以将输入数据转换为指定的数据类型，并返回转换后的数据
ploy_reg = PolynomialFeatures(degree=3)
# 特征处理
x_ploy = ploy_reg.fit_transform(x_data)
# 定义回归模型
lin_reg = LinearRegression()
# 训练模型
lin_reg.fit(x_ploy, y_data)

 degree的值越大，模型会更加拟合

 画图

# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, lin_reg.predict(ploy_reg.fit_transform(x_data)), c='r')
plt.title('Truth or Bluff (Polynomial Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()

标准方程法（梯度下降法的变化）

矩阵微积分（维基百科）

https://en.wikipedia.org/wiki/Matrix_calculus#Scalar-by-vector_identities 

 

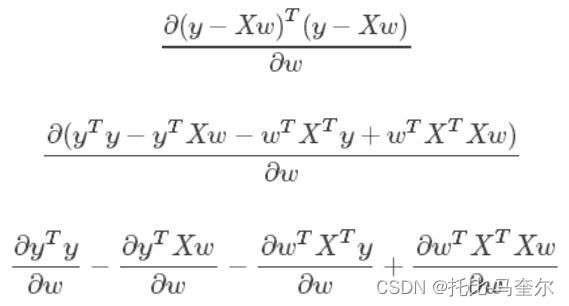
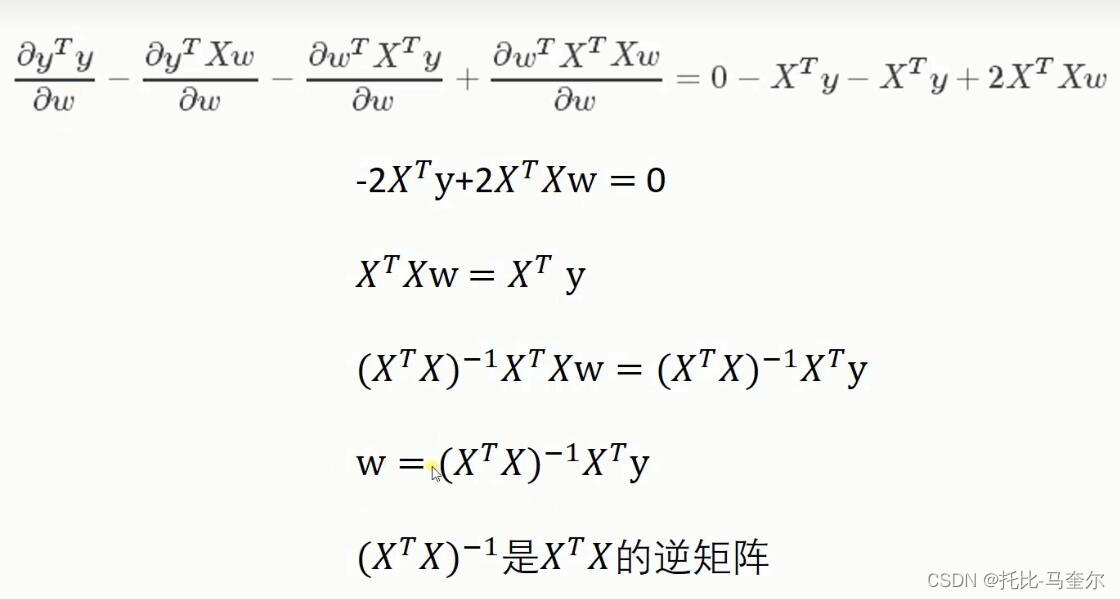
时间复杂度约为O（n^3） ；n是特征数量

 w是线性模型参数，用于计算结果。一般用theta代替。权重值越大，对于结果的影响越大。

b表示偏差。线性回归的目标是找到一组最佳的w和b值，使得预测值与实际值之间的误差平方和最小。因此，要求w的值是为了找到这组最佳的w和b值，使得预测值与实际值之间的误差平方和最小

矩阵不可逆的情况

1.线性相关的特征

2.特征数据太多（样本数m<=特征数量n） 

线性回归-标准方程法

import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0,np.newaxis]
y_data = data[:,1,np.newaxis]
plt.scatter(x_data,y_data)
plt.show()

 添加偏置项的作用

  1. 改善模型的泛化能力：在机器学习模型中，如果特征矩阵X中存在一些特征的取值为0或者大部分为0，那么在训练过程中，这些特征将无法对模型的训练产生任何贡献。这是因为在标准线性回归模型中，偏置项b的存在使得模型可以适应那些取值为0或者大部分为0的特征。当特征的取值范围更大时，添加偏置项可以使得模型更好地拟合训练数据，提高模型的泛化能力。
  2. 避免模型过拟合：在一些情况下，当特征的取值范围很大时，如果不添加偏置项，模型可能会过度拟合训练数据，导致在测试集上的表现很差。而添加偏置项可以使得模型的训练更加稳定，避免模型过拟合。
# np.mat函数接受一个数组作为参数，并返回一个矩阵对象
# shape属性是一个元组，描述了矩阵的行数和列数
print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
# 给样本添加偏置项
# 创建一个长度为100的一维数组，全部元素都是1（np.ones((100,1))），
# 然后将其与原数组x_data在列方向上拼接（即第一列前面加一列全是1的列）
X_data = np.concatenate((np.ones((100,1)),x_data),axis=1)
print(X_data.shape)

标准方程法求解回归参数

# 标准方程法求解回归参数
def weights(xArr, yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    xTx = xMat.T*xMat  #矩阵乘法
    # 计算矩阵的值，如果值为0，说明该矩阵没有逆矩阵
    if np.linalg.det(xTx) == 0.0:
        print("This matrix cannot do inverse")
        return
    # xTx.I为xTx的逆矩阵
    ws = xTx.I*xMat.T*yMat
    return ws
ws = weights(X_data,y_data)
print(ws)

 画图

# 画图
# 该数组包含两个元素，每个元素都是一个包含单个整数的列表。
x_test = np.array([[20],[80]])
y_test = ws[0] + x_test*ws[1]
plt.plot(x_data, y_data, 'b.')
plt.plot(x_test, y_test, 'r')
plt.show()

特征缩放

数据归一化

把数据的取值范围处理为0--1或者-1--1之间；

任意数据转化为0--1之间：

newValue = (oldValue-min)/(max-min)

任意数据转化为-1--1之间：

newValue = ((oldValue-min)/(max-min)-0.5)*2

 均值标准化

x为特征数据，u为数据的平均值，s为数据的方差

newValue = (oldValue-u)/s

 一般是-0.5左右到0.5左右

交叉验证法

通过将原始数据集进行切分，得到不同的训练集和测试集，用训练集训练模型，用测试集评估模型的泛化能力。交叉验证法可以有效地防止过拟合和欠拟合，评估模型的泛化能力，选择最佳的模型和参数

过拟合、正确拟合和欠拟合

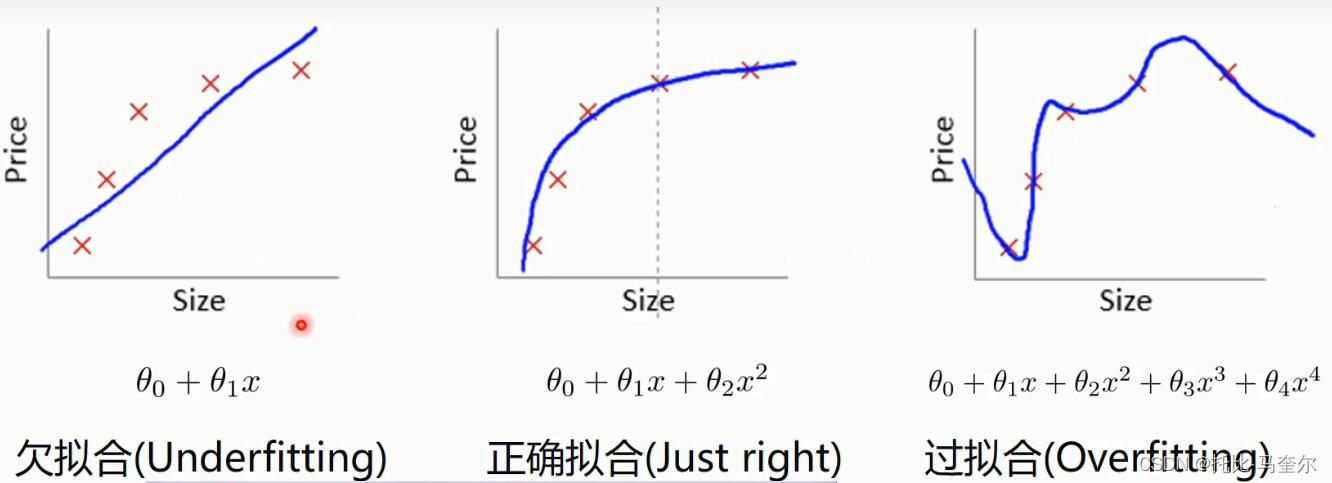
过拟合的主要表现是：在训练集中表现得很好，但是在测试集中表现得不够好

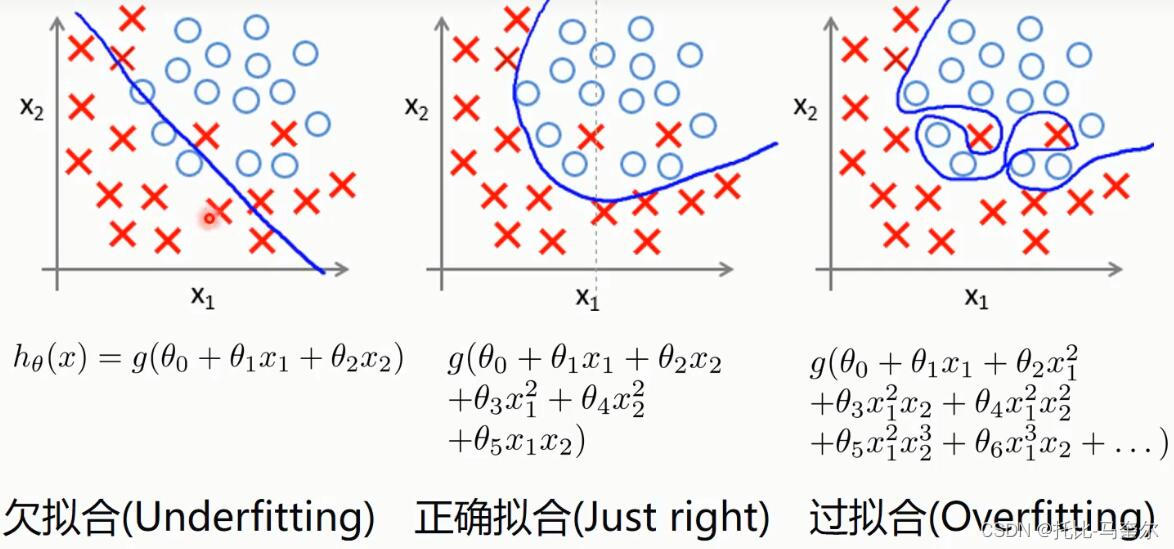
 防止过拟合的方法

1.减少特征（简化模型）

2.增加数据量

3.正则化

正则化代价函数 

 θj指的就是多项式的系数；也就是权重

岭回归（标准方程法、有偏估计）

岭回归最早使用处理特征数多于样本的情况，现在也用于在估计中加入偏差，从而得到更好的估计。同时也可以解决多重共线性的问题。

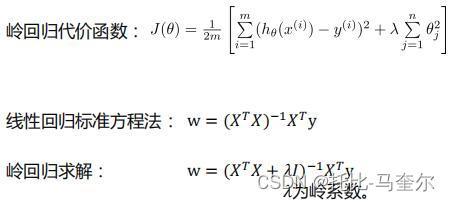
岭回归在估计中加入偏差

如果数据的特征数量比样本还多，则计算逆矩阵时会出错。 

θj指的就是多项式的系数，也就是w 

岭回归的代价函数 ，其中λ是正则项的系数，不是岭系数

λ和残差平方和之间的关系是，当λ越大，正则化项的权重就越大，模型的复杂性就越低，越倾向于选择更简单的模型，从而降低过拟合的风险

随着λ的增大，特征的系数会被"压缩"，即每个特征的系数都会比没有正则化时更接近于0。这种"压缩"效应会导致模型的复杂性降低，从而降低过拟合的风险。然而，这种"压缩"效应也会导致模型的预测能力下降，因此残差平方和也会随之增加。

sklearn-岭回归

import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt
# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
# 因为第一列的第一个是空值，所以默认填充为Nan
print(data)
# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)

 创建模型

# 创建模型
# 默认生成50个值
alphas_to_test = np.linspace(0.001, 1)
print(alphas_to_test)
# 创建模型，保存误差值
# Ridge指的是岭回归，CV指的是交叉验证
# alphas指的是岭回归系数，主要就是用交叉验证去验证这些数字是否正确
model = linear_model.RidgeCV(alphas=alphas_to_test, store_cv_values=True)
# store_cv_values=True: 设置为True时会存储交叉验证过程中每个阿尔法值的评分。
# 这可以用于后续评估和比较不同阿尔法值的性能
model.fit(x_data, y_data)

# 岭系数
print(model.alpha_)
# loss值
print(model.cv_values_.shape)
# 16次测试集，50个岭系数

画图

# 画图
# 岭系数和loss值的关系      .mean(axis=0)指的是16个测试集loss值的平均值
plt.plot(alphas_to_test, model.cv_values_.mean(axis=0))
# 选取的岭系数值的位置
plt.plot(model.alpha_, min(model.cv_values_.mean(axis=0)),'ro')
plt.show()

标准方程法-岭回归

import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt

# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
# 因为第一列的第一个是空值，所以默认填充为Nan
print(data)

# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1,np.newaxis]
print(x_data)
print(y_data)
print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
# 给样本添加偏置项
X_data = np.concatenate((np.ones((16,1)),x_data),axis=1)
print(X_data.shape)

 标准方程法求解回归参数

# 岭回归标准方程法求解回归参数
def weights(xArr, yArr, lam=0.2):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    xTx = xMat.T*xMat  #矩阵乘法
    # xMat.shape[1]获取矩阵xMat的列数，然后np.eye()用这个列数来创建一个相应大小的单位矩阵
    rxTx = xTx + np.eye(xMat.shape[1])*lam
    # 计算矩阵的值，如果值为0，说明该矩阵没有逆矩阵
    if np.linalg.det(rxTx) == 0.0:
        print("This matrix cannot do inverse")
        return
    # xTx.I为xTx的逆矩阵
    ws = rxTx.I*xMat.T*yMat
    return ws
ws = weights(X_data,y_data)
print(ws)

 LASSO算法

通过构造一个一阶惩罚函数获得一个精炼的模型；通过最终确定一些指标（变量）的系数为零（岭回归估计系数等于零的机会微乎其微）

擅长处理具有多重共线性的数据，与岭回归一样是有偏估计

sklearn-LASSO

import numpy as np
from numpy import genfromtxt
from sklearn import linear_model

# 读入数据 
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)

# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)

 创建模型

# 创建模型
model = linear_model.LassoCV()
model.fit(x_data, y_data)

# lasso系数
print(model.alpha_)
# 相关系数
print(model.coef_)

弹性网

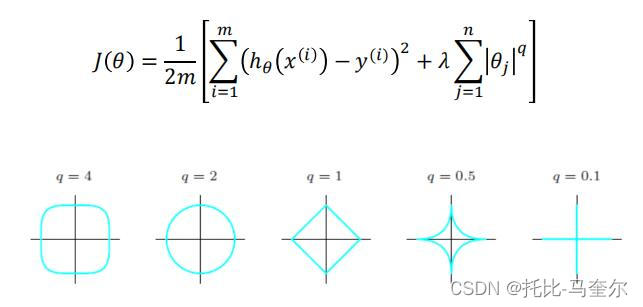
 而具体的弹性网指的是

 sklearn-弹性网

import numpy as np
from numpy import genfromtxt
from sklearn import linear_model

# 读入数据 
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)

# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)

创建模型

# 创建模型
model = linear_model.ElasticNetCV()
model.fit(x_data, y_data)

# 弹性网系数
print(model.alpha_)
# 相关系数
print(model.coef_)

 相关系数

线性函数的值越接近1，整个的线性相关性就越强

相关系数是用来描述两个变量之间的线性关系的，但决定系数的适用范围更广，可以用于描述非线性或者有两个及两个以上自变量的相互关系

非凸函数和凸函数

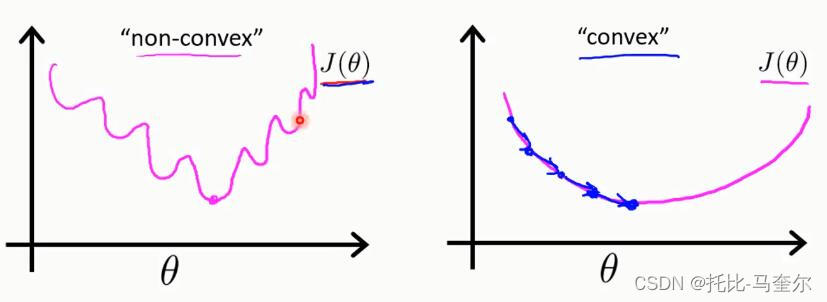
 线性回归的代价函数是凸函数

单位矩阵

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1212674.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

谷粒商城项目-环境配置

谷粒商城项目-环境配置

安装vegrant 2.2.18 注意vritual box&#xff08;6.1.30&#xff09;和vegrant版本兼容 初始化和创建虚拟机 vagrant init centos/7 vagrant up连接虚拟机 vegrant ssh解决vagrant up速度过慢问题 https://app.vagrantup.com/centos/boxes/7/versions/2004.01直接下载对应镜像…
阅读更多...
大数据-之LibrA数据库系统告警处理（ALM-12047 网络读包错误率超过阈值）

大数据-之LibrA数据库系统告警处理（ALM-12047 网络读包错误率超过阈值）

告警解释 系统每30秒周期性检测网络读包错误率&#xff0c;并把实际错误率和阈值&#xff08;系统默认阈值0.5%&#xff09;进行比较&#xff0c;当检测到网络读包错误率连续多次&#xff08;默认值为5&#xff09;超过阈值时产生该告警。 用户可通过“系统设置 > 阈值配置…
阅读更多...
kubernetes集群编排——istio

kubernetes集群编排——istio

官网&#xff1a;https://istio.io/latest/zh/about/service-mesh/ 部署 [rootk8s2 ~]# tar zxf istio-1.19.3-linux-amd64.tar.gz [rootk8s2 ~]# cd istio-1.19.3/[rootk8s2 istio-1.19.3]# export PATH$PWD/bin:$PATH demo专为测试准备的功能集合 [rootk8s2 istio-1.19.3]# i…
阅读更多...
基于JavaWeb+SSM+社区居家养老服务平台—颐养者端微信小程序系统的设计和实现

基于JavaWeb+SSM+社区居家养老服务平台—颐养者端微信小程序系统的设计和实现

基于JavaWebSSM社区居家养老服务平台—颐养者端微信小程序系统的设计和实现 源码获取入口前言主要技术系统设计功能截图Lun文目录订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 源码获取入口 前言 在复杂社会化网络中&#xff0c;灵活运用社会生活产生的大数据&am…
阅读更多...
msvcp120.dll下载_msvcp120.dll文件丢失解决[dll系统文件修复]

msvcp120.dll下载_msvcp120.dll文件丢失解决[dll系统文件修复]

msvcp120.dll是Microsoft Visual C库中的一个重要组件&#xff0c;属于Microsoft Visual C 2005 Redistributable Package。它提供了许多用于执行C程序所需的函数。Visual C是一款流行的集成开发环境&#xff08;IDE&#xff09;&#xff0c;广泛应用于游戏、视频和图形处理等领…
阅读更多...
PVE虚拟机下如何安装自定义备份Win系统镜像文件

PVE虚拟机下如何安装自定义备份Win系统镜像文件

环境： Virtual Environment 7.3-3 Win s2019 UltraISO9.7 USM6.0 NTLite_v2.1.1.7917 问题描述： PVE虚拟机下如何安装自定义备份Win系统镜像文件 解决方案： 方法一 1.在需要备份的系统上使用SGI工具备份系统最后生成.wim文件 2.用软碟通把.wim文件保存为.iso文件…
阅读更多...
2023年【北京市安全员-B证】试题及解析及北京市安全员-B证证考试

2023年【北京市安全员-B证】试题及解析及北京市安全员-B证证考试

题库来源&#xff1a;安全生产模拟考试一点通公众号小程序 北京市安全员-B证试题及解析根据新北京市安全员-B证考试大纲要求&#xff0c;安全生产模拟考试一点通将北京市安全员-B证模拟考试试题进行汇编&#xff0c;组成一套北京市安全员-B证全真模拟考试试题&#xff0c;学员…
阅读更多...
硬件开发笔记（十一）：Altium Designer软件介绍、安装过程和打开pcb工程测试

硬件开发笔记（十一）：Altium Designer软件介绍、安装过程和打开pcb工程测试

若该文为原创文章&#xff0c;转载请注明原文出处 本文章博客地址&#xff1a;https://hpzwl.blog.csdn.net/article/details/134405411 红胖子网络科技博文大全&#xff1a;开发技术集合&#xff08;包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软硬…
阅读更多...
PostGIS学习教程七：关于几何图形的练习

PostGIS学习教程七：关于几何图形的练习

文章目录 一、函数列表二、练习 一、函数列表 以下是我们迄今为止看到的所有函数的汇总&#xff0c;它们应该对练习有用&#xff01; sum(expression) aggregate to return a sum for a set of records count(expression) aggregate to return the size of a set of records …
阅读更多...
Go语言fyne开发桌面应用程序-环境安装

Go语言fyne开发桌面应用程序-环境安装

环境安装 参考https://developer.fyne.io/started/#prerequisites网站 之前的文章介绍了如何安装GO语言这里不在叙述 msys2 首先安装msys2&#xff0c;https://www.msys2.org/ 开始菜单打开MSYS2 执行 $ pacman -Syu$ pacman -S git mingw-w64-x86_64-toolchain注意&#…
阅读更多...
差分信号的末端并联电容到底有什么作用？

差分信号的末端并联电容到底有什么作用？

差分信号的末端并联电容到底有什么作用&#xff1f; 在现代电子系统中&#xff0c;差分信号是一种常见的信号形式&#xff0c;它们通过两根互补的信号线传输信号&#xff0c;具有较低的噪声和更高的抗干扰能力。然而&#xff0c;当差分信号线长度较长或者遇到复杂的电路环境时&…
阅读更多...
golang学习笔记——类型转换

golang学习笔记——类型转换

Go 语言类型转换 将整型转换为浮点型&#xff1a; var a int 10 var b float64 float64(a)将字符串变量 str 转换为整型变量 num var str string "10" var num int num, _ strconv.Atoi(str)注意&#xff0c;strconv.Atoi 函数返回两个值&#xff0c;第一个是转…
阅读更多...
场景图形管理 - （2）

场景图形管理 - （2）

裁剪平面示例(二) 裁剪平面(osg::Scissor)示例(二)的代码如程序清单8-2所示 // 裁剪平面测试&#xff08;2&#xff09; void scissor_8_2(const string strDataFolder) { osg::ref_ptr<osgViewer::Viewer> viewer new osgViewer::Viewer(); osg::ref_ptr<osg::Gra…
阅读更多...
甲方与三方渗透团队的协作注意点

甲方与三方渗透团队的协作注意点

文章目录 以下是优化后的内容&#xff1a; 作为甲方安全团队主导的渗透攻击&#xff0c;以下几点需要注意&#xff1a; 预备充分 与测试团队协调&#xff0c;提供乙方攻击所需的必要资源&#xff0c;以及具有甲方特色的资源。例如&#xff0c;如果认为自己的权限系统需要重点评…
阅读更多...
JSON vs. CSV vs. YAML vs. XML vs. HDF5vs. XLS：数据格式之争

JSON vs. CSV vs. YAML vs. XML vs. HDF5vs. XLS：数据格式之争

前言 数据处理是现代计算机科学和信息技术中至关重要的一部分。有效地选择和处理数据格式是数据科学、工程和各种应用中的关键环节。本文将深入探讨各种常见数据格式及其Python库的应用&#xff0c;旨在帮助读者更好地理解和应用这些数据格式&#xff0c;以及如何选择最适合自…
阅读更多...
UE5 - UI Material Lab 学习笔记

UE5 - UI Material Lab 学习笔记

1、学习资料收集 UI Material Lab : https://www.unrealengine.com/marketplace/zh-CN/product/ui-material-lab 视频1&#xff1a;https://www.bilibili.com/video/BV1Hm4y1t7Kn/?spm_id_from333.337.search-card.all.click&vd_source707ec8983cc32e6e065d5496a7f79ee6 视…
阅读更多...
FDTD自定义材料

FDTD自定义材料

官方原文档链接 该文档内容摘自原文档及相关链接 从txt导入材料数据 各项同性材料的3Dmaterials数据 txt文件中应包含以下三列。第一列为波长或频率&#xff1b;第二列为折射率或介电常数实部&#xff1b;第三列为折射率或介电常数虚部。 420 5.08894 0.237724 440 4.78…
阅读更多...
性能测试场景的设计方法

性能测试场景的设计方法

作者&#xff5c;李文&#xff0c;自如-质量中心 来源&#xff5c;自如技术公众号 背景 引用&#xff1a;根据2008年Aberdeen Group的研究报告&#xff0c;对于Web网站&#xff0c;1秒的页面加载延迟相当于少了11%的PV&#xff08;page view&#xff09;&#xff0c;相当于降低…
阅读更多...
Unity--互动组件（Toggle Group）||Unity--互动组件（Slider）

Unity--互动组件（Toggle Group）||Unity--互动组件（Slider）

Toggle Group 属于同一组的切换开关受到限制&#xff0c;因此一次只能打开其中一个开关&#xff0c;按下其中一个开关时&#xff0c;其他的开关将会自动关闭&#xff1b; Allow Switch Off&#xff1a;&#xff08;允许关闭&#xff09; 如果禁用此设置&#xff0c;则按下当前…
阅读更多...
Hadoop的概述

Hadoop的概述

1、Hadoop的发展史&#xff1a; Google首先发布三篇文章&#xff1a;GFS(Google File System)、Mapreduce&#xff08;计算引擎&#xff09;、Bigtable &#xff0c;随着时间的推移&#xff1a; hadoop1.0与2.0 的区别是在2.0的版本中出现了yarn&#xff0c;主要是负责资源的调…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023