Tag

【位运算】

---

题目来源

201. 数字范围按位与

---

题目解读

计算给定区间内所有整数的按位与的结果。

---

解题思路

本题朴素的方法是直接将区间内的所有整数按位与，时间复杂度为 $O(n)$，数据量已经达到 $10^{1}0$，必然超时。接下来介绍两种不会超时的方法。

方法一：公共前缀

先来说说什么是公共前缀，公共前缀指的是所有需要按位与计算的数对应的二进制数从高位到低位公共的二进制字符。比如 [9, 12] 的公共前缀为 0000 1，解释如图所示：

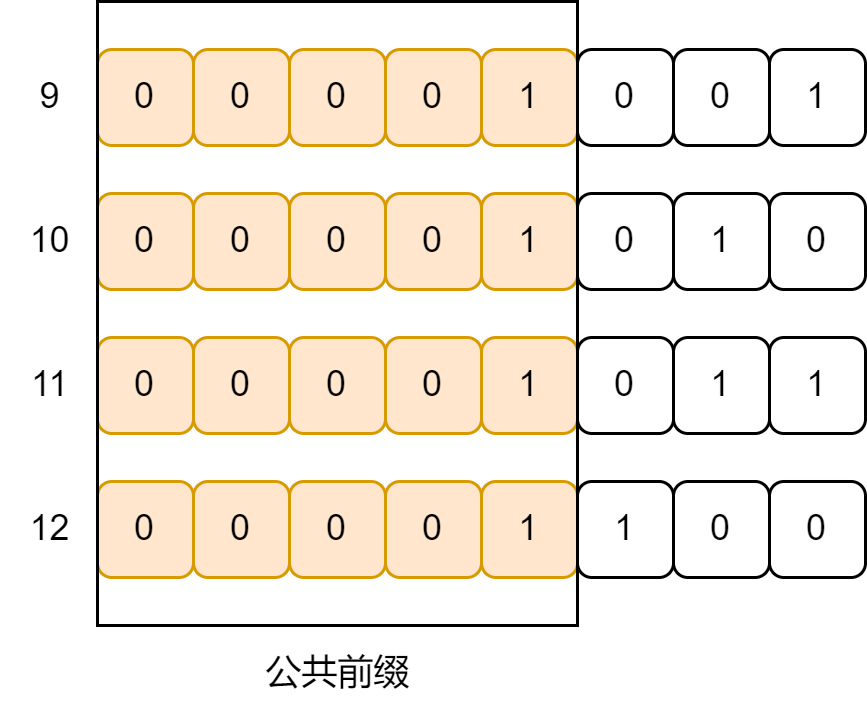
根据上图，我们发现连续数字按位与的值等于公共前缀后面再补上剩余的 0。 这个规律正确吗？我们来证明一下。假设对于连续区间内所有数的二进制数，前 i 位（从高位开始数）均相同，第 i+1 位开始不同，由于区间 [m, n] 连续，所以区间内从小到大先枚举出来的数的第 i+1 位为 0，枚举出来相对靠后数的第 i+1 位全部为 1。 并且一定存在连续的两个数 x 和 x+1 满足 x 的第 i+1 位为 0，后面全为 1，x+1 的第 i+1 位为 1，后面全为 0，对应上图中的例子即为 11 和 12。这种形如 0111… 和 1000… 的二进制串的按位与的结果一定为 0000…，因此第 i+1 位开始的剩余位均为 0，前 i 位由于均相同，因此按位与结果不变。最后的答案即为二进制字符串的公共前缀再用零补上后面的剩余位。

实现代码

class Solution {
public:
    int rangeBitwiseAnd(int left, int right) {
        int res = 0;
        for (int i = 0; i < 32; ++i) {
            for (int num = left; num <= right; ++num) {
                res |= num & 1;
                num >>= 1;
            }
        }
        return res;
    }
};

复杂度分析

时间复杂度：$O(logn)$，$n$ 为 right 的值、

空间复杂度：$O(1)$。

方法二：n & (n-1)

根据方法一，我们知道需要保留的是区间 [m, n] 中的公共前缀，也就是去掉非公共前缀的部分，我们可以使用 n & (n-1) 来去除，直到 m = n，最后返回 n 即可。于是有代码：

实现代码

class Solution {
public:
    int rangeBitwiseAnd(int m, int n) {
        while (m < n) {
            n &= (n-1);
        }
        return n;
    }
};

复杂度分析

时间复杂度：$O(logn)$，$n$ 为 right 的值、

空间复杂度：$O(1)$。

---

写在最后

如果文章内容有任何错误或者您对文章有任何疑问，欢迎私信博主或者在评论区指出 💬💬💬。

如果大家有更优的时间、空间复杂度方法，欢迎评论区交流。

最后，感谢您的阅读，如果感到有所收获的话可以给博主点一个 👍 哦。