偶然看到一篇paper(2018年发表),说GMP中的素性检测使用的是单独的Miller_Rabin方法,单独的Miller_Rabin素性检测会存在部分安全问题(低概率),然后突然想求证一下最新版本的GMP中是否进行了修改。python中常用的gmpy库的底层实际就是GMP实现的。
文章目录
- 1.源码追踪
- 1.1 相关版本
- 1.2 介绍
- 1.3 源码分析
- 总结
1.源码追踪
1.1 相关版本
- gmpy 2.1.0 https://github.com/BrianGladman/gmpy2
- GMP 6.2.1 https://github.com/alisw/GMP
1.2 介绍
gmpy2 是一个 Python 库,用于进行高精度整数、有理数和浮点数的计算。它是对 GNU Multiple Precision Arithmetic Library(GMP)的 Python 封装,使得在 Python 中可以方便地进行大整数、有理数和浮点数的运算。gmpy2 支持大整数的基本算术运算、比较、位操作等,同时也支持有理数的计算,包括有理数的加减乘除、比较和约分等操作。此外,gmpy2 还支持浮点数的高精度计算,包括浮点数的加减乘除、取整、取模、取幂等操作。gmpy2 库还提供了一些高级功能,例如素数检测、质因数分解、离散对数计算、椭圆曲线加密等。gmpy2 库的使用非常方便,可以直接在 Python 中导入 gmpy2 模块,然后使用其中的函数和类进行高精度计算。
GNU Multiple Precision Arithmetic Library(GMP)是一个用于高精度整数运算的 C 语言库。它提供了高效的多精度算术运算和相关函数,可以进行大整数和大有理数的运算,包括加法、减法、乘法、除法、取模等操作。GMP 还支持高精度浮点数的运算,包括浮点数的加减乘除、开方、对数、指数等操作。GMP 库被广泛应用于密码学、加密算法、数值计算、大数据处理等领域,因为它能够提供比标准整数和浮点数类型更高的精度和范围。GMP 是一个开源项目,可以在多种平台上使用,并且有多种语言的绑定,如 Python 的 gmpy2、Perl 的 Math::GMP 等。
1.3 源码分析
在https://github.com/BrianGladman/gmpy2/blob/HEAD/src/gmpy2_mpz_misc.c#L1348处,是gmpy2.is_prime()的实现,可以发现主要是调用了GMP的mpz_probab_prime_p方法

在GMP的https://github1s.com/alisw/GMP/blob/master/mpz/pprime_p.c#L50-L51处,是GMP的mpz_probab_prime_p方法的实现,可以在末尾看到,确实调用的是mpz_millerrabin这样一个函数的实现。
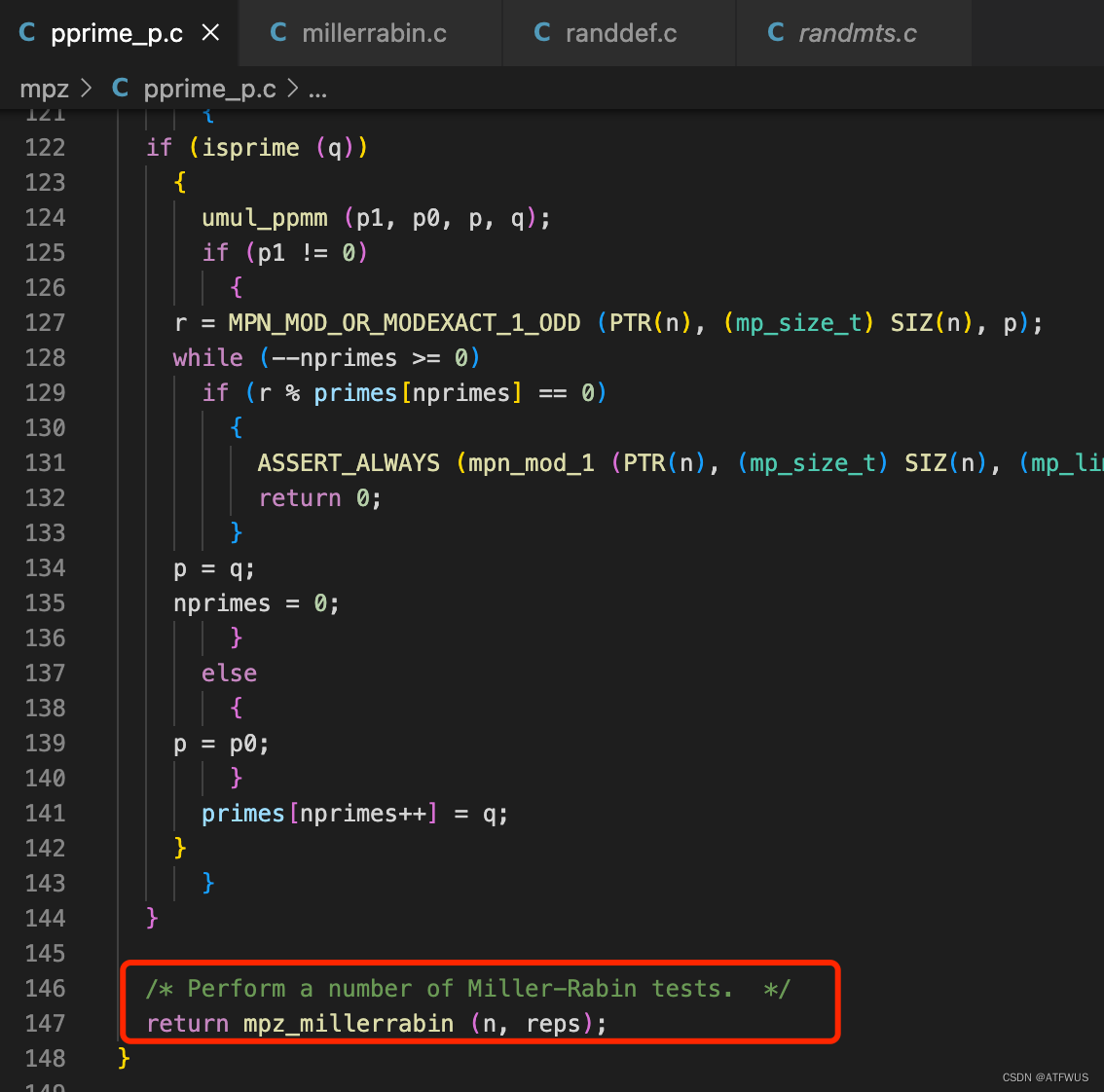
继续跟进该函数, 可以发现,虽然名字叫mpz_millerrabin,但实际使用的是Baillie-PSW的测试方法,也就是同时使用Miller-Rabin测试和Lucas测试,这种测试方法目前还没有较好的生成伪素数的方法。
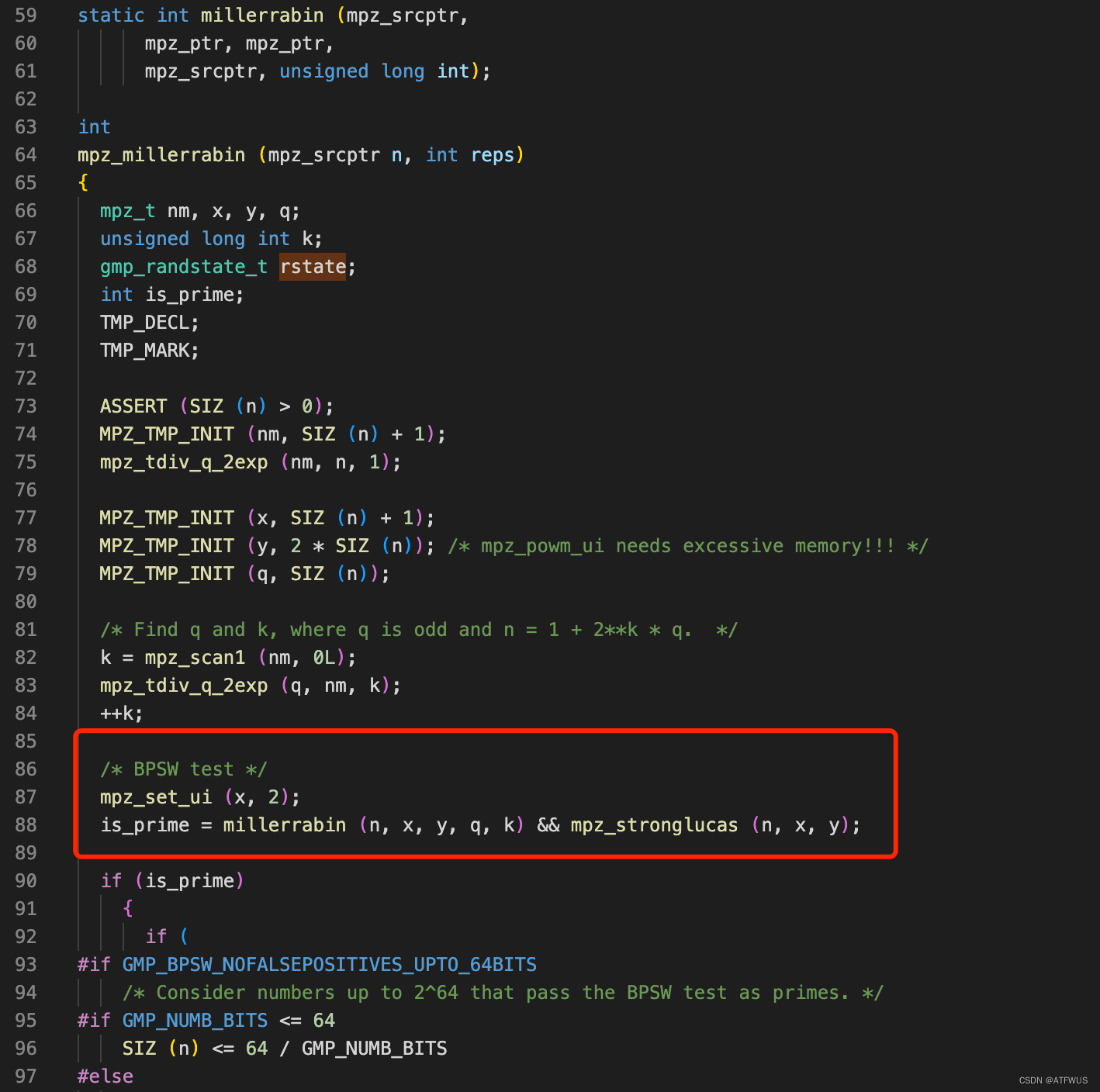
总结
GMP6.2.1 底层素性校验使用的是BSPW方法,具有较好的安全性。
在伪随机数生成去不可控的前提下,没有较好的生成能通过BSPW测试的伪素数的方法。
ATFWUS 2023-11-14