学Diffusion前需要储备的一些知识点

自学Diffusion是非常困难的，尤其是到了VAE和VI这里基本找不到比较好的中文资料，甚至是涉及到一些重参数化，高斯混合之类的问题摸不着来龙去脉。在本文中，基本不会涉及公式，只有intuition和理解，如果要看公式的话可以移步到其他博主文章。

Auto-encoder

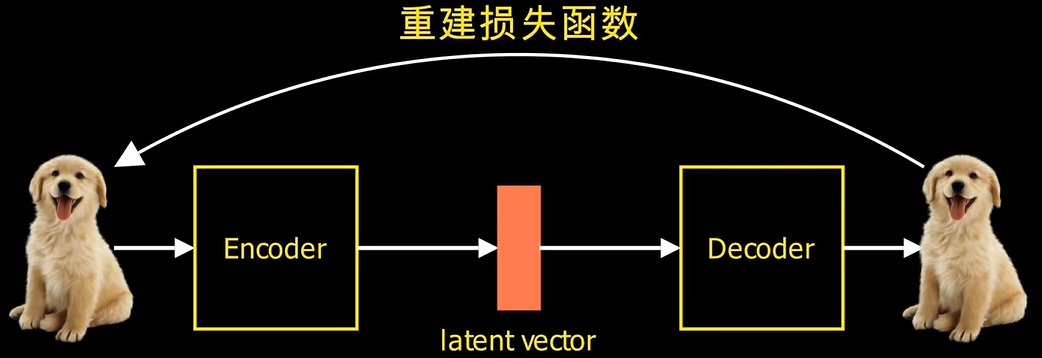
自编码器的“自”不是自动，而是自己训练，即自监督学习。Auto-encoder是自监督学习的一种，其可以理解为一个试图还原其原始输入的系统。它和PCA的道理是一样的，只不过将PCA的转换矩阵W和WT换成encoder和decoder。主成分分析（PCA）和自编码器（AutoEncoders, AE）是无监督学习中的两种代表性方法。两者都是非概率方法。它演化出了很多有意思的工作：去水印，AI抠图，替换背景等。

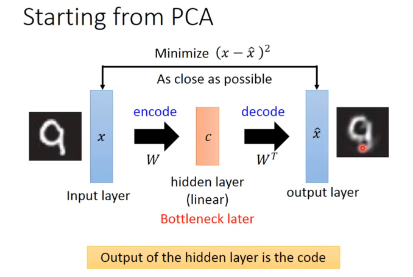
当你没有接触过AE时，需要明白：

为什么要encoder原始输入？答：数据总归是有规律的，其中却隐含着大量的特征信息，需要将重要的信息挖掘出来。
训练时是不需要label的，用一个损失实现输入输出相减就行。训练完之后decoder就没用了，目的只是为了得到encoder。如果想要做分类任务，在encoder后边接一个分类器就能完成分类工作。
如果说从原始数据X压缩到Z之后信息已经损失了，为什么还要用decoder恢复到X~？况且，本来最后也用不到decoder？答：让Auto-encoder有据可依。可以这样说，encoder把成绩从100～0分成了优良中差，既然Z是瓶颈，恢复到X~时确实已经丢失信息了，优不知道对应91还是99了，但是，仍然要Reconstruct到X~的意义是，有个参照来矫正，用X~和目标X对比，至少还在九十多分，而不会到六十分以下。

De-noising Auto-encoder

普通的Auto-encoder的区别在于，Encoder的输入并不是原始的图像，而是将图像加上一定的噪声之后再作为Encoder的输入，而在输出的时候是要求Decoder输出能够与未加噪声之前的图像越接近越好。

Variational auto-encoder

从AE到VAE的进化：假设原始数据为一张人脸图像X，它有512*512个维度。AE的编码器将X编码为N维的隐变量Z，Z的每一维对应一个特征（比如表情、肤色、发型等），每一维上的值表示样本F在这种特征上的取值。也就是说，AE是将样本编码为N个固定的特征值，用来描述输入图像X在每个潜在特征的表现，每个特征值在对应的特征空间下是一个离散值。

重点来了：因为神经网络只能去做learn过的事情，所以AE的解码器，只能基于潜在特征隐变量Z的每个出现过的数值去恢复图像。比如，AE只学习过"smile"的特征值为0.99的恢复过程，那碰到"smile"的特征值为0.88时，AE的解码器是没有能力去恢复的，此时就可能预测一个错误的图像，不一的就是人脸了。也就是说，在每一个特征空间中，对于训练过程中没有涵盖过的地方，AE的解码器没办法去decode。

进一步，无论是AE，DAE，还是MAE，本质上都是学习bottleneck处的这个隐变量特征Z，然后拿Z去做检测、分割、分类等下游任务。抛开下游任务不说，AE的decoder不能叫做生成，原因就是中间特征Z是一个用于重建的固定特征，即使DAE或MAE等技术可以使得中间特征Z的范围变大，这也只是让离散特征值的数量变多而已，他们是永远不可能占满整个特征空间的。当隐变量Z是一个概率分布时，就可以touch到整个特征空间，这样就可以基于特征空间中的任何一个特征值来生成图像，这样才能称为真正的生成。

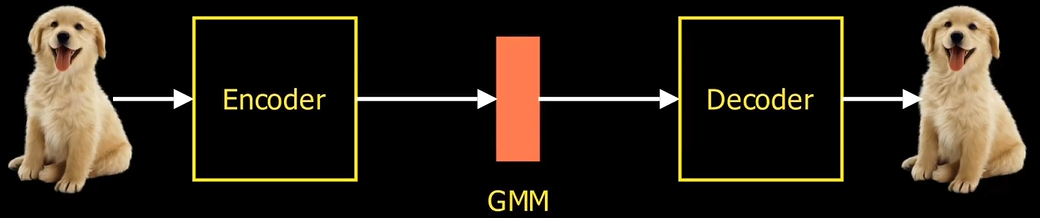
假设隐变量Z不是一个固定的特定值，而是一个分布（严谨来讲是一个联合分布，在每一个特征维度上学到的都是一个分布），那么经过训练后，解码器就会知道"面对学到的一个分布，应该生成什么样的图像"，而之前的AE经过训练后，解码器知道的是"面对学到的一个特征值，应该生成什么样的图像"。"面对学到的一个分布，应该生成什么样的图像"的意思是：只要特征值属于这个分布，那么"解码器"就可以对它进行解码，这无疑极大地扩大了解码器的“知识范围”。那么当我们想生成样本的时候，只要给出一个这个分布下的特征值，解码器就会进行生成，当这个特征值是"见"过的时，生成的是老样本，当这个特征值是"没见"过的时，生成的就是新样本。基于此，VAE应运而生，它在中间不再生成一个固定的编码特征，而是生成一个分布（高斯）。本质上是增大隐变量Z在特征空间上的范围，从而使解码器能access整个特征空间，拥有真正的生成能力（对任意特征值都可生成）。

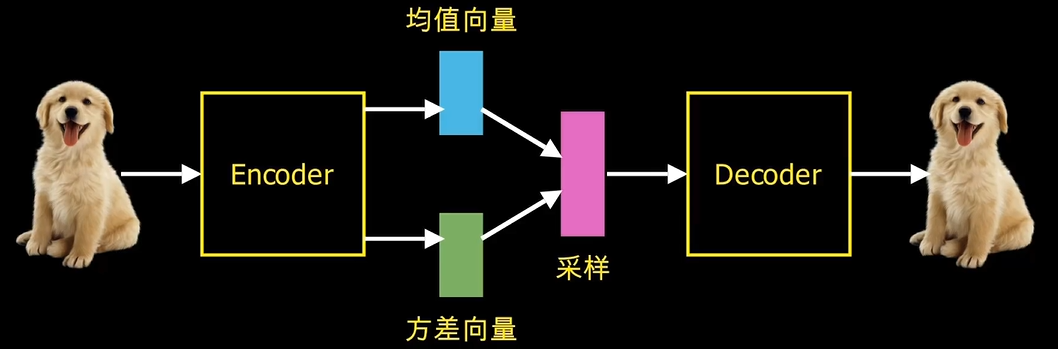
VAE不再把输入映射到固定的变量上，而是映射到一个分布上，比如混合高斯GMM。网络中的bottleneck被分解为两个向量。一个叫做均值向量。一个叫做方差向量。损失函数较AE复杂了一些：第一块是重建损失，这个和自编码器是相同的。后面一项是KL散度，用来描述学习的分布和高斯分布之间的相似性。VAE可以理解为从这个高斯分布取样的任一点，输出后都和输入相似，使隐空间更加平滑。

VAE这样复杂的模型在pytorch中也就是简简单单几行代码：定义模型；实验参数；数据集。然后就开始训练了。这两年除了被用于图像压缩，图像降噪，图像分割，也被应用于强化学习用来进行环境的潜在空间表示，从高维的观测数据中有效提取特征。

下面就对VAE的原理进行详细分析：

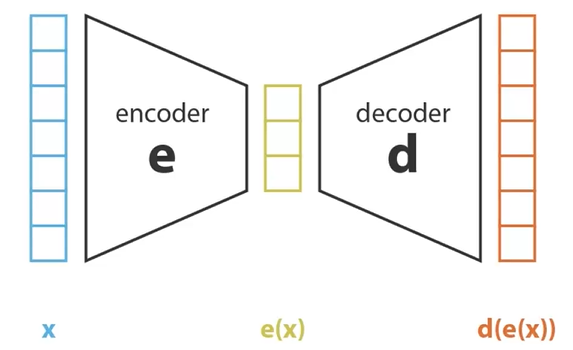
VAE的本质非常近似于数据生成，和AIGC的关系非常非常紧密。e(x)是一个平滑(regularized)的隐空间。在训练VAE时，是用数据集让他重新生成他自己，但使用的时候又不需要encoder，直接用隐空间随便采样一个样本，就可以生成一张之前没有见过的新图。这也是和AE不用decoder，而用encoder做下游任务的一个不同的点。

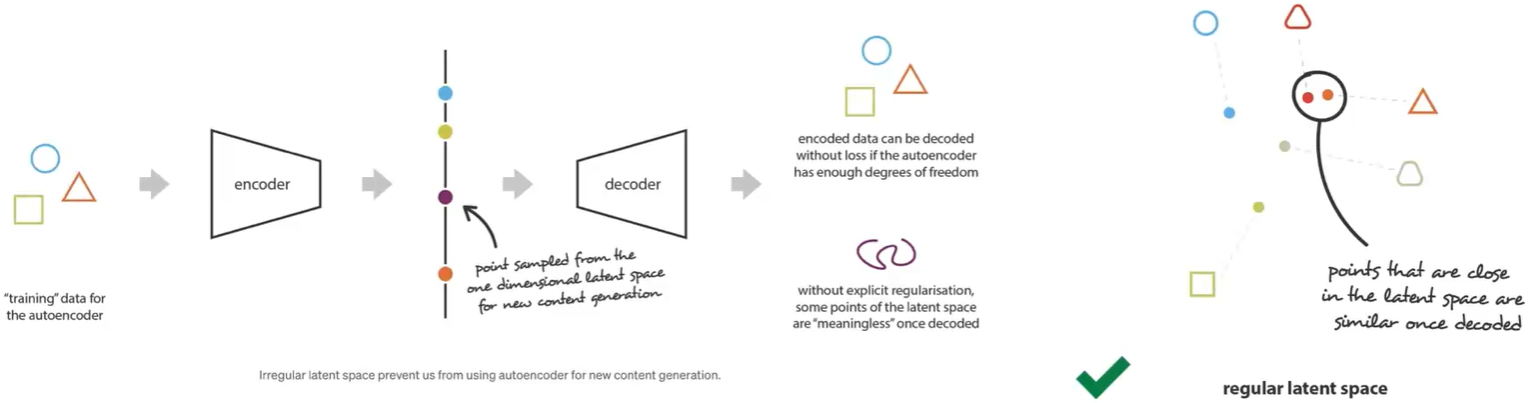
什么是隐空间，为什么需要隐空间？基于AIGC的思想，最左边的圆形三角形和正方形再通过encoder和docoder后我们并不关心是否会recover成圆形，正方形和三角形。我们想生成的是不是三角形，又有点像三角形一样的具有随机性的东西。如果隐空间中采样了像图中紫色点一样潜在样本，则decoder出来的一定是很不规则的或者是noise的东西。这是因为训练的本质是用loss来更改decoder和encoder中的参数，而且这是一个overfitting的过程。因为圆形必须要recover成圆形，正方形必须要recover成正方形。所以在训练的过程中网络对于真正的隐空间或者内部的参数压根不关心，我们只关心这个结果。所以隐空间会overfit它map过来的蓝点，黄点以及红点，中间的紫点没有loss去regular就会非常的杂乱。但VAE真正想要的是最右边的结果，即：假设在隐空间中采样的点离三角形和圆形比较近，则需要生成一个圆角三角形。因此，就需要通过一系列的方法让隐空间变的平滑，使得即使decoder即使没有见过这样的input或者prompt，但还能比较好的生成一个合理的结果。

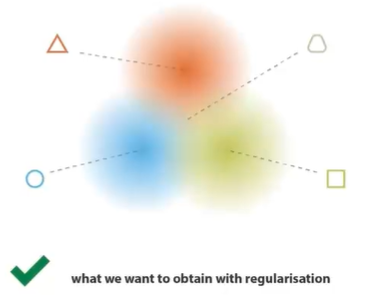
VAE和概率有什么关系？首先要思考的是如果要自己来实现一个平滑的隐空间模型，会怎么办？首先需要确定的是训练的东西还是一堆图片，loss就是让他recover自己。那大佬是怎么做的：既然想要隐空间中的每一个点都有含义，那就引入概率或者随机性，使得同样的输入x，每次得到的z=e(x)都不同。而这个z是有一个概率分布的，输入红色三角形，大概率是中间的那个点，但也有可能是旁边的点。这样随着不断的训练，z就慢慢的把整个空间给平滑掉。那如何通过数学的方式让训练从确定性变为不确定的呢？答案是用两个损失函数去逼近和模拟 $p(x|z)$ 和 $p(z|x)$ 两个概率分布，并保证 $p(z)$ 和 $p(z|x)$ 是平滑的。

loss是什么？什么是VI？既然是逼近两个概率分布，那什么叫做概率分布的距离？因为如果没有距离的概念，就没有办法谈逼近。而且这个距离的计算必须简单且可导，这样才能去做gradient descent。Variational Inference (Vl)就是一套让两个概率分布逼近的方法，且计算简单，它能够为VAE提供一个loss的计算方法。
VI和KL Divsergence？什么叫概率分布最像(最近)，那就是：随机生成同样的内容的概率有多相似。假设现在有三个分布，再假设有一段序列112112111212，则可以分别计算出不同分布生成这个序列的可能性：1:0.5^12~=2.4X E-4；2:0.05^8X0.95^4 =3.1 X E-11；3.0.518X0494=26XE-4。可以看出第一个和第三个分布比较相似。

回到如何比较两个分布的相似度的问题，直观的做法是把他们的概率相除，比值大的就不相似，比值小的就相似。然后再把该式log一下，就得到了KL Divsergence：

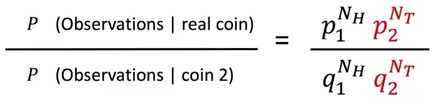
接下来就需要用 KL Divsergence写出loss表达式：定义encoder network为 $q_{\theta }(z)$ ，我们需要做的是让encoder network去逼近 $p(z|x)$ 。 $p(z|x)$ 代表自然界真实的概率分布，实际上这人是不知道的，所以只能用encoder network去逼近。他们两个的KL散度计算过程如下所示。

可能有人会问为什么不去研究KL散度的最小化，而要去研究将ELBO最大化：因为 $logp(x)$ 是不太可能被算出来的，它所表示的是从全世界的图片中选择一张输入到网络中的概率是多少。这就是为什么将logp(x)单独腾挪出来的原因。但又由于 $X$ 是我们的数据集，相对于 $z$ 来说已经是一个常量了。所以要使得KL散度最小，则ELBO最大即可。在神经网络的设计中，paper的作者通常要给出 $p(x,z)$ 和 $q_\theta (z)$ 两个函数的解析式， $\theta$ 通常为神经网络的参数，再通过VI来确定最优参数，让 $q_\theta (z)$ 接近 $p(x,z)$ 。不同的 $q_\theta (z)$ 与真实的 $p(z|x)$ 差距可能会非常大。
VAE是怎么把这一堆串起来的？首先，VAE的初衷是：用两个损失函数去逼近和模拟 $p(x|z)$ 和 $p(z|x)$ 两个概率分布，并保证 $p(z)$ 和 $p(z|x)$ 是平滑的。首先，作者定义了 $p(z)$ 是高斯的，为了规范期间，作者将encoder记作 $q_{\theta }(z|x)=N(g(x),h(x))$ ，将decoder记作 $p_{\theta }(z|x)=N(f(z),cI)$ ， $\theta$ 为神经网络的参数。将这两个带入到ELBO中，则是要找到g，h，f三个network使得ELBO最大。

那么就直接可以写loss了，只要loss变小，上面这个式子变大，那么就能满足要求了，而不是说一定要是一样的：

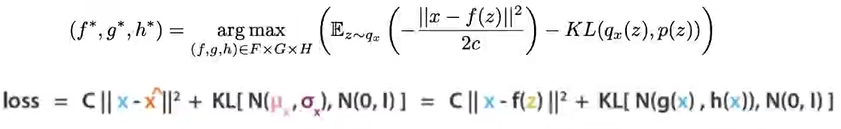
最后就是神经网络的构建了：h为通过x来算variant，g为通过x来算mean，f就是通过隐空间的采样值z来生成具体的图像。

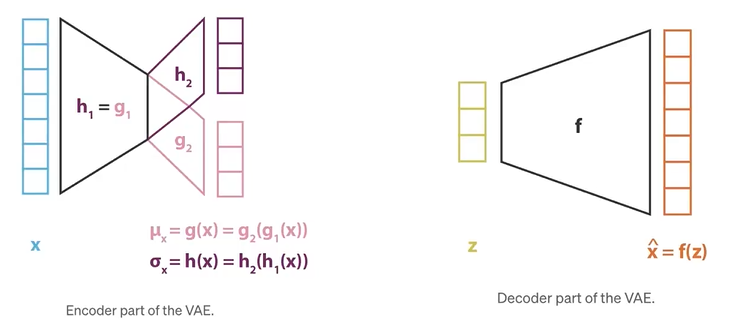
Reparametrisation Trick

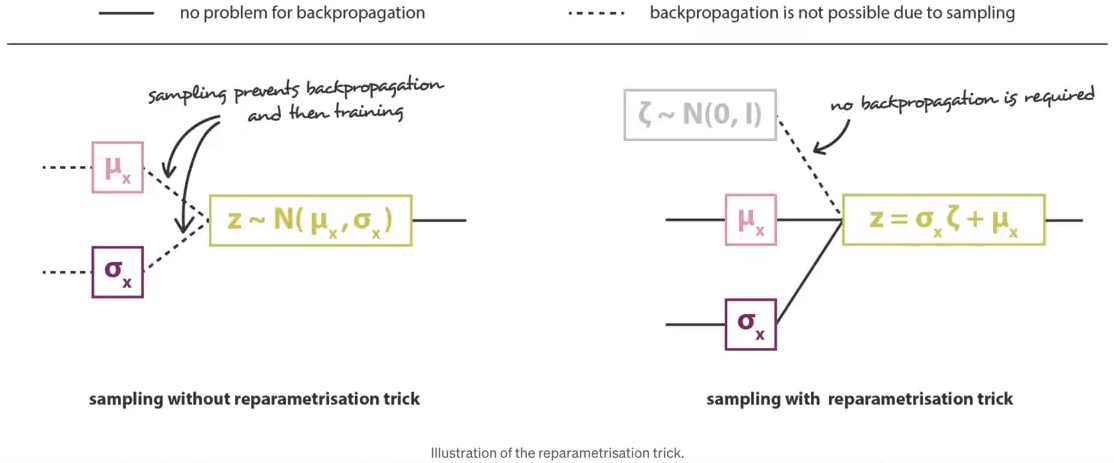
神经网络在back propagate的过程中实际上是通过求偏微分方程将loss去propagate到每一个factor。但这有一个前提是pipeline是确定的，如果pipeline是随机的则就无法做back propagate了。encoder的生成结果只有两组数值，也就是normal distribution的mean和variant。而z是在这个混合高斯中随机选了一个样本。这样我们就没有办法通过z这里的difference对mean和variant进行偏微分的计算。但如果用了Reparametrisation Trick，既将高斯分布改写成右边的形式，将改写后的公式进行偏微分，就可以将z这里的difference去back propagate到mean和variant上了。

VAE的用法：plugin到别的network里面去，把两个组件之间的隐空间平滑掉。

高斯混合模型（Gaussian Mixed Model）

从模型角度看它一个生成式模型，从几何角度看，是多个高斯分布函数的线性组合。假设现在有 $K$ 个高斯分布： $N(x|\mu _{1},\sigma_{1}^{2})$ ， $N(x|\mu _{2},\sigma_{2}^{2})$ ， $N(x|\mu _{3},\sigma_{3}^{2})$ ··· $N(x|\mu _{k},\sigma_{k}^{2})$ ，且 $N(x|\mu _{k},\sigma_{k}^{2})=\frac{1}{\sqrt{2\Pi }\sigma _{k}}e^{-\frac{(x-\mu ^{k})^{2}}{2\sigma _{k}^{2}}}$ ，他们占整个高斯混合模型的比例依次为： $\alpha _{1}$ ， $\alpha _{2}$ ， $\alpha _{3}$ ··· $\alpha _{k}$ ， $\sum_{k=1}^{k}\alpha _{k}=1$ 。则 $P(x|\theta)=\sum_{k=1}^{k}\alpha _{k}N(x|\mu _{k},\sigma_{k}^{2})$ 为一个高斯混合模型。其中 $\theta$ 为高斯混合模型中的 2K 个参数（ $\mu_{i}$ 和 $\sigma _{i}$ ）， $x$ 就代表观测结果。

如果我们有一堆样本，知道每一个样本服从什么高斯分布，则很容易将每个分布的 $\mu_{i}$ 和 $\sigma _{i}$ 都求出来。但事情是没有这么简单的，实际上，我们拿到一堆样本并不知道它们服从上述的哪个高斯分布。假设这些observed variable为： $x_{1}$ ， $x_{2}$ ， $x_{3}$ ··· ， $x_{n}$ 。隐变量 $z$ 为对应样本 $x$ 服从什么分布，即 $x\sim z$ 。 $z$ 为离散随机变量： $P(z=c_{k})=p_{k}$ （下面EM算法要用到）。需要明确的是： $x$ 可以服从混合模型中的任何一个具体的高斯分布，这类似于软分类，因此才需引入隐变量 $z$ 概率的概念。
高斯混合模型的目的为：依据隐变量 $z$ 的辅助，估计高斯混合模型中所有高斯分布的参数 $\mu_{i}$ 和 $\sigma _{i}$ 。
高斯混合模型的生成为：先采样得到哪一个具体的高斯模型，再在这个具体的高斯模型中采样具体的样本。重复N次就得到了N个样本。
当我们引入了隐变量 $Z$ ，要表示 $P(x)$ 时，通常会选择积分的方式将其积掉，如 $P(x)=\int_{}^{}P(x,z)dz$ ，因为 $z$ 是离散随机变量，积分改求和则为： $P(x)=\sum_{z}P(x,z)=\sum_{k=1}^{K}P(x,z=c_{k})=\sum_{k=1}^{K}P(z=c_{k})P(x|z=c_{k})=\sum_{k=1}^{K}p_{k}\cdot N(x|\mu _{k},\sigma _{k})$ ， $c_{k}$ 为其中一个高斯模型。

那么如何求这个高斯模型呢，即如何求参数 $\theta =p_{1},p_{2},\cdots,p_{k},\mu_{1},\mu_{2},\cdots,\mu_{k},\sigma_{1},\sigma_{2},\cdots,\sigma_{k}$ ，即利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。极大似然估计是一个能想到的点，但结论是无法求出解析解的。设observed data $X=(x_{1},x_{1},\cdots,x_{N})$ 和 latent variable $z$ ，则有complete data为 $(x_{1},z_{1}),(x_{2},z_{2}),\cdots,(x_{N},z_{N})$ 。则 $\hat{\theta }_{MLE}=argmaxlogP(X)=\prod_{i=1}^{N}P(x_{i})=argmax\sum_{1}^{N}logP(x_{i})=\sum_{1}^{N}log\sum_{k=1}^{K}p_{k}\cdot N(x_{i}|\mu _{k},\sigma _{k})$ ，因为log里是连加而不是连乘，求导后是得不到解析解的。MLE解单一高斯问题是没问题的，此处得从其他方法解，即EM（最大期望）算法。如何做呢？本来还想写来着，但是后面还有一堆，这里就不写了，截个图意思意思。学扩散模型，我们只要知道有这回事就够了。

KL散度额外补充

KL 散度，人工智能领域超级常用的一个技术，是一个用来衡量两个概率分布的相似性的一个度量指标。在现实世界中，任何观察都可以看成表示成信息和数据，一般来说，我们无法获取数据的总体而只能拿到数据的部分样本，根据数据的部分样本，我们会对数据的整体做一个近似的估计，而数据整体本身有一个真实的分布（我们可能永远无法知道）。那么近似估计的概率分布和数据整体真实的概率分布的相似度，或者说差异程度，可以用 KL 散度来表示。公式如下：

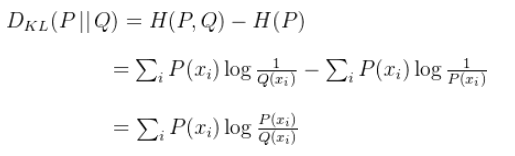
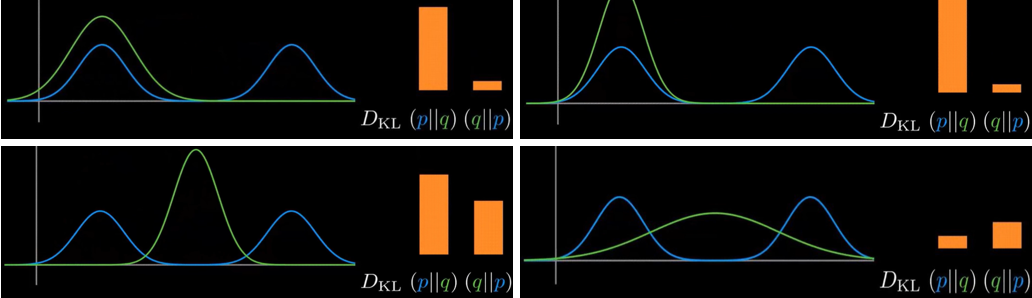
在深度学习领域中，P一般指样本在训练集中的概率分布（这是一个真实分布），Q一般指样本在网络预测结果中的概率分布（这是一个近似分布），利用KL散度，我们可以精确地计算出当我们近似一个分布与另一个分布时损失了多少信息。因为对数函数是凸函数，所以KL散度是非负的。当Q 越接近P，KL散度就越小，只有当P与Q处处相等时才会等于0。

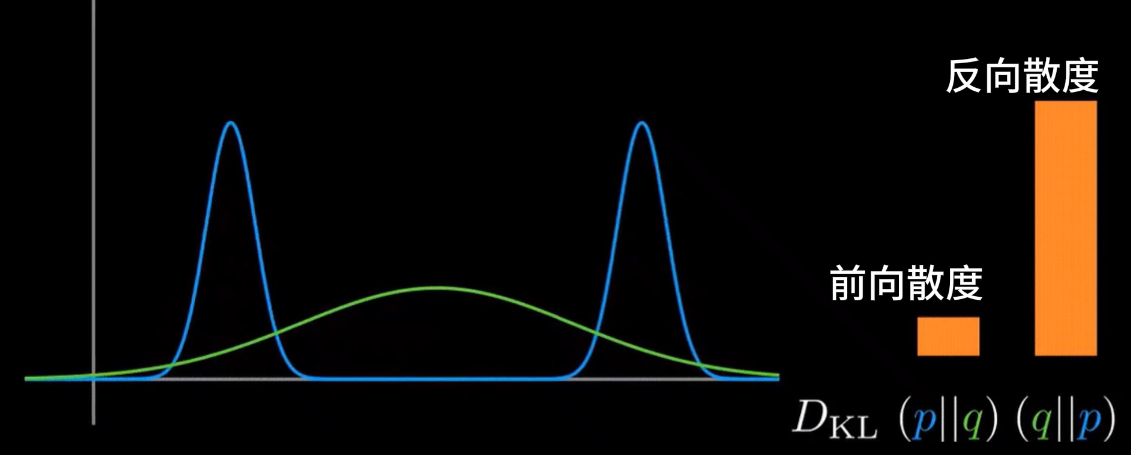
$D_{KL}=(p|q)$ 叫做分布p相对于q的散度， $D_{KL}=(q|p)$ 叫做分布q相对于p的散度。谁在前，就关注谁多一点。就像是生活中，每个人总对自己在意的地方给予更高的权重。若真实分布为q，拟合分布为q，则 $D_{KL}=(p|q)$ 叫做前向散度，在监督学习中有大量的应用。 $D_{KL}=(q|p)$ 叫做反向散度，在强化学习和变分推断中有大量的应用。