8.2 BA 与图优化
Bundle Adjustment 是指从视觉图像中提炼出最优的 3D 模型和相机参数(内参和外参)。
8.2.1 相机模型和 BA 代价函数
我们从一个世界坐标系中的点 p \boldsymbol{p} p 出发,把相机的内外参数和畸变都考虑进来,最后投影成像素坐标,步骤如下:
(1)世界坐标系转换到相机坐标系
P ′ = R p + t = [ X ′ , Y ′ , Z ′ ] T (8-30) \boldsymbol{P'}=\boldsymbol{Rp}+\boldsymbol{t}=[X',Y',Z']^\mathrm{T} \tag{8-30} P′=Rp+t=[X′,Y′,Z′]T(8-30)
(2)将 P ′ \boldsymbol{P'} P′ 投影至归一化平面,得到归一化坐标
P c = [ u c , v c , 1 ] T = [ X ′ / Z ′ , Y ′ / Z ′ , 1 ] T (8-31) \boldsymbol{P}_c=[u_c, v_c, 1]^{\mathrm{T}}=[X'/Z',Y'/Z', 1]^\mathrm{T} \tag{8-31} Pc=[uc,vc,1]T=[X′/Z′,Y′/Z′,1]T(8-31)
(3)去畸变(这里仅考虑径向畸变)
{
u
c
′
=
u
c
(
1
+
k
1
r
c
2
+
k
2
r
c
4
)
v
c
′
=
v
c
(
1
+
k
1
r
c
2
+
k
2
r
c
4
)
(8-32)
\left\{\begin{array}{l} u_{\mathrm{c}}^{\prime}=u_{\mathrm{c}}\left(1+k_{1} r_{\mathrm{c}}^{2}+k_{2} r_{\mathrm{c}}^{4}\right) \\ v_{\mathrm{c}}^{\prime}=v_{\mathrm{c}}\left(1+k_{1} r_{\mathrm{c}}^{2}+k_{2} r_{\mathrm{c}}^{4}\right) \end{array}\right. \tag{8-32}
{uc′=uc(1+k1rc2+k2rc4)vc′=vc(1+k1rc2+k2rc4)(8-32)
(4)根据内参模型,计算像素坐标
{ u s = f x u c ′ + c x v s = f y v c ′ + c y (8-33) \left\{\begin{array}{l} u_{s}=f_{x} u_{\mathrm{c}}^{\prime}+c_{x} \\ v_{s}=f_{y} v_{\mathrm{c}}^{\prime}+c_{y} \end{array}\right. \tag{8-33} {us=fxuc′+cxvs=fyvc′+cy(8-33)
上面的过程也就是 观测方程,将它抽象的记为
z = h ( x , y ) (8-34) \boldsymbol{z}=h({\boldsymbol{x},\boldsymbol{y}}) \tag{8-34} z=h(x,y)(8-34)
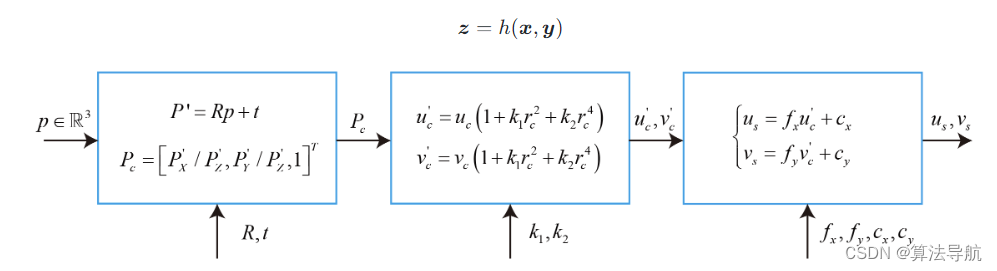
其中, x \boldsymbol{x} x 是指此时相机的位姿,即 R \boldsymbol{R} R、 t \boldsymbol{t} t,对应的李群为 T \boldsymbol{T} T,李代数为 ξ \boldsymbol{\xi} ξ;路标 y \boldsymbol{y} y 即三维点 p \boldsymbol{p} p;观测数据 z \boldsymbol{z} z 则是像素坐标。以最小二乘角度考虑,此次观测的误差为:
e = z − h ( T , p ) (8-35) \boldsymbol{e}=\boldsymbol{z}-h(\boldsymbol{T},\boldsymbol{p}) \tag{8-35} e=z−h(T,p)(8-35)
把其他时刻的观测都考虑进来,设 z i j \boldsymbol{z}_{ij} zij 为在位姿 T i \boldsymbol{T}_i Ti 处观察路标 p j \boldsymbol{p}_j pj 产生的数据,那么整体的代价函数为
1 2 ∑ i = 1 m ∑ j = 1 n ∥ e i j ∥ 2 = 1 2 ∑ i = 1 m ∑ j = 1 n ∥ z i j − h ( T i , p j ) ∥ 2 (8-36) \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{n}\|\boldsymbol{e}_{ij}\|^2=\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{n}\|\boldsymbol{z}_{ij}-h(\boldsymbol{T}_i,\boldsymbol{p}_j)\|^2 \tag{8-36} 21i=1∑mj=1∑n∥eij∥2=21i=1∑mj=1∑n∥zij−h(Ti,pj)∥2(8-36)
对这个最小二乘进行求解,相当于对位姿和路标同时进行优化,也就是所谓的 BA。
8.2.2 BA 的求解
容易看出 h ( T , p ) h(\boldsymbol{T},\boldsymbol{p}) h(T,p) 不是线性函数,因此我们希望采用非线性优化的方法求解最优值,所以关键在于梯度 Δ x \Delta \boldsymbol{x} Δx 的求解。
在整体 BA 目标函数上,我们把自变量定义为所有待优化的变量:
x = [ T 1 , T 2 , . . . , T m , p 1 , p 2 , . . . , p n ] T (8-37) \boldsymbol{x}=[\boldsymbol{T}_1,\boldsymbol{T}_2,...,\boldsymbol{T}_m,\boldsymbol{p}_1,\boldsymbol{p}_2,...,\boldsymbol{p}_n]^T \tag{8-37} x=[T1,T2,...,Tm,p1,p2,...,pn]T(8-37)
相应地,增量方程中的 Δ x \Delta \boldsymbol{x} Δx 是对整体自变量的增量。当我们给自变量一个增量时,目标函数变为:
1 2 ∥ f ( x + Δ x ) ∥ 2 ≈ 1 2 ∑ i = 1 m ∑ j = 1 n ∥ e i j + F i j Δ ξ i + E i j Δ ξ j ∥ 2 (8-38) \frac{1}{2}\|f(\boldsymbol{x}+\Delta \boldsymbol{ x})\|^2 \approx \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{n}\|\boldsymbol{e}_{ij}+\boldsymbol{F}_{ij} \Delta \boldsymbol{\xi}_i+\boldsymbol{E}_{ij}\Delta \boldsymbol{\xi}_j\|^2 \tag{8-38} 21∥f(x+Δx)∥2≈21i=1∑mj=1∑n∥eij+FijΔξi+EijΔξj∥2(8-38)
其中, F i j \boldsymbol{F}_{ij} Fij 表示整个代价函数在当前状态下对相机位姿 ξ \boldsymbol{\xi} ξ 的偏导数, E i j \boldsymbol{E}_{ij} Eij 表示整个代价函数在当前状态下路标位置 p \boldsymbol{p} p 的偏导数。
把相机位姿放在一起
x c = [ ξ 1 , ξ 2 , . . . , ξ m ] T ∈ R 6 m (8-39) \boldsymbol{x}_c=[ \boldsymbol{\xi}_1,\boldsymbol{\xi}_2,...,\boldsymbol{\xi}_m]^\mathrm{T} \in \mathbb{R}^{6m} \tag{8-39} xc=[ξ1,ξ2,...,ξm]T∈R6m(8-39)
把空间点的变量也放在一起:
x p = [ p 1 , p 2 , . . . , p n ] T ∈ R 3 n (8-40) \boldsymbol{x}_p=[ \boldsymbol{p}_1,\boldsymbol{p}_2,...,\boldsymbol{p}_n]^\mathrm{T} \in \mathbb{R}^{3n} \tag{8-40} xp=[p1,p2,...,pn]T∈R3n(8-40)
那么,式(8-38)可简化为
1 2 ∥ f ( x + Δ x ) ∥ 2 ≈ 1 2 ∥ e + F Δ x c + E Δ x p ∥ 2 (8-41) \frac{1}{2}\|f(\boldsymbol{x}+\Delta \boldsymbol{ x})\|^2 \approx \frac{1}{2}\|\boldsymbol{e}+\boldsymbol{F} \Delta \boldsymbol{x}_c+\boldsymbol{E}\Delta \boldsymbol{x}_p\|^2 \tag{8-41} 21∥f(x+Δx)∥2≈21∥e+FΔxc+EΔxp∥2(8-41)
上式将二次项之和写成了矩阵形式。这里的雅克比矩阵 F \boldsymbol{F} F 和 E \boldsymbol{E} E 是整体目标函数对整体变量的导数,它是一个很大的矩阵,由每个误差项的导数 F i j \boldsymbol{F}_{ij} Fij 和 E i j \boldsymbol{E}_{ij} Eij 拼凑而成。可以采用高斯牛顿法或 L-M 法,得到增量方程
H Δ x = g (8-42) \boldsymbol{H} \Delta \boldsymbol{x}=\boldsymbol{g} \tag{8-42} HΔx=g(8-42)
为便于表示,我们将变量归类为位姿和空间点两种,则雅克比矩阵分块为
J = [ F E ] (8-43) \boldsymbol{J=[F \quad E]} \tag{8-43} J=[FE](8-43)
以高斯牛顿法为例,则 H \boldsymbol{H} H 矩阵为
H = J T J = [ F T F F T E E T F E T E ] (8-44) \boldsymbol{H}=\boldsymbol{J}^{\mathrm{T}} \boldsymbol{J}=\left[\begin{array}{ll} \boldsymbol{F}^{\mathrm{T}} \boldsymbol{F} & \boldsymbol{F}^{\mathrm{T}} \boldsymbol{E} \\ \boldsymbol{E}^{\mathrm{T}} \boldsymbol{F} & \boldsymbol{E}^{\mathrm{T}} \boldsymbol{E} \end{array}\right] \tag{8-44} H=JTJ=[FTFETFFTEETE](8-44)
但是,这个矩阵的维度非常大,而且直接对 H \boldsymbol{H} H 求逆,复杂度也很高。所以我们需要利用 H \boldsymbol{H} H 矩阵的特殊结构,加速计算过程。
8.2.3 稀疏性和边缘化
(1) H \boldsymbol{H} H 矩阵的稀疏性是由雅克比矩阵 J ( x ) \boldsymbol{J}(\boldsymbol{x}) J(x) 引起的。考虑其中一个 e i j \boldsymbol{e}_{ij} eij,它只描述了相机在 T i \boldsymbol{T}_i Ti 处看到 p j \boldsymbol{p}_j pj这件事,只与第 i i i个位姿和第 j j j 个路标有关,而与其他位姿和路标都无关,因此对其余部分的变量的导数都为零。所以误差 e i j \boldsymbol{e}_{ij} eij 对应的雅克比矩阵为
J i j ( x ) = ( 0 2 × 6 , … 0 2 × 6 , ∂ e i j ∂ T i , 0 2 × 6 , … 0 2 × 3 , … 0 2 × 3 , ∂ e i j ∂ p j , 0 2 × 3 , … 0 2 × 3 ) (8-45) \boldsymbol{J}_{i j}(\boldsymbol{x})=\left(\mathbf{0}_{2 \times 6}, \ldots \boldsymbol{0}_{2 \times 6}, \frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{T}_{i}}, \mathbf{0}_{2 \times 6}, \ldots \mathbf{0}_{2 \times 3}, \ldots \mathbf{0}_{2 \times 3}, \frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{p}_{j}}, \mathbf{0}_{2 \times 3}, \ldots \mathbf{0}_{2 \times 3}\right) \tag{8-45} Jij(x)=(02×6,…02×6,∂Ti∂eij,02×6,…02×3,…02×3,∂pj∂eij,02×3,…02×3)(8-45)
注意,误差对相机位姿的偏导 ∂ e i j / ∂ ξ i \partial \boldsymbol{e}_{i j} / \partial \boldsymbol{\xi}_{i} ∂eij/∂ξi 维度为 2 × 6 2\times6 2×6,对路标点的偏导 ∂ e i j / ∂ p j \partial \boldsymbol{e}_{i j} / \partial \boldsymbol{p}_{j} ∂eij/∂pj维度为 2 × 3 2\times3 2×3。
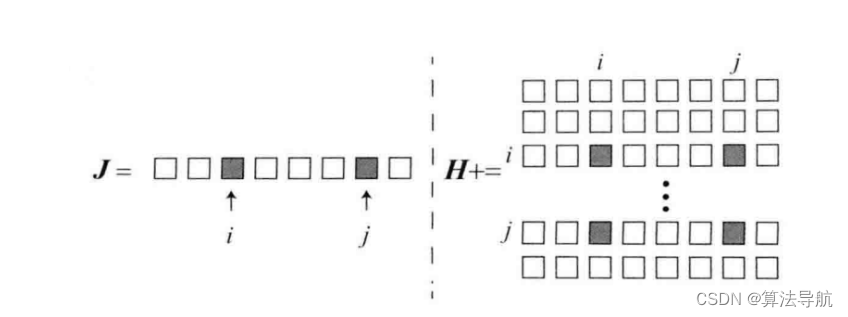
(2)以下图为例,假设 J i j \boldsymbol{J}_{ij} Jij 只在 i i i、 j j j 处有非零块,那么它对 H \boldsymbol{H} H矩阵的贡献为 J i j T J i j \boldsymbol{J}_{ij}^\mathrm{T}\boldsymbol{J}_{ij} JijTJij, J i j T J i j \boldsymbol{J}_{ij}^\mathrm{T}\boldsymbol{J}_{ij} JijTJij 矩阵有 4 个非零块,位于 ( i , i ) (i,i) (i,i)、 ( i , j ) (i,j) (i,j)、 ( j , i ) (j,i) (j,i)、 ( j , j ) (j,j) (j,j)。对整体的 H \boldsymbol{H} H,有
H = ∑ i , j J i j T J i j (8-46) \boldsymbol{H}=\sum_{i,j}\boldsymbol{J}_{ij}^\mathrm{T}\boldsymbol{J}_{ij} \tag{8-46} H=i,j∑JijTJij(8-46)
将 H \boldsymbol{H} H 矩阵分块
H = [ H 11 H 12 H 21 H 22 ] (8-47) \boldsymbol{H}=\left[\begin{array}{ll} \boldsymbol{H}_{11} & \boldsymbol{H}_{12} \\ \boldsymbol{H}_{21} & \boldsymbol{H}_{22} \end{array}\right] \tag{8-47} H=[H11H21H12H22](8-47)
结合式(8-44)可知, H 11 \boldsymbol{H}_{11} H11 只和相机位姿有关, H 22 \boldsymbol{H}_{22} H22 只和路标点有关。当遍历矩阵 H \boldsymbol{H} H时,总有:
① H 11 \boldsymbol{H}_{11} H11 是对角矩阵,且只在 H i i \boldsymbol{H}_{ii} Hii 处有非零块;
② H 22 \boldsymbol{H}_{22} H22 也是对角矩阵,且只在 H j j \boldsymbol{H}_{jj} Hjj处有非零块;
③ H 12 \boldsymbol{H}_{12} H12 和 H 21 \boldsymbol{H}_{21} H21 可能是稀疏的,也可能是稠密的,视具体观测数据而定。
(3)以下图为例
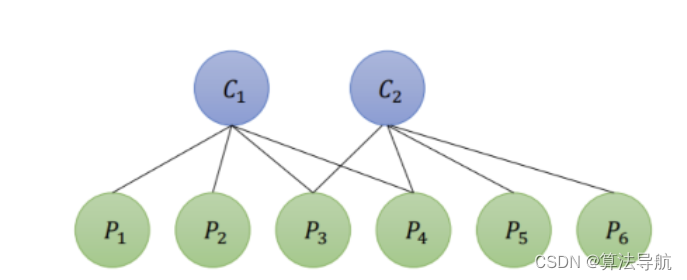
假设一个场景内,有 2 个相机位姿( C 1 \boldsymbol{C}_1 C1、 C 2 \boldsymbol{C}_2 C2)和 6 个路标点( P 1 \boldsymbol{P}_1 P1、 P 2 \boldsymbol{P}_2 P2、 P 3 \boldsymbol{P}_3 P3、 P 4 \boldsymbol{P}_4 P4、 P 5 \boldsymbol{P}_5 P5、 P 6 \boldsymbol{P}_6 P6),这些相机位姿和路标点所对应的变量为 T i , i = 1 , 2 \boldsymbol{T}_{i}, i=1,2 Ti,i=1,2 和 p j , j = 1 , 2 \boldsymbol{p}_{j}, j=1,2 pj,j=1,2。可以推出,此场景下的 BA 目标函数为:
1 2 ( ∥ e 11 ∥ 2 + ∥ e 12 ∥ 2 + ∥ e 13 ∥ 2 + ∥ e 14 ∥ 2 + ∥ e 23 ∥ 2 + ∥ e 24 ∥ 2 + ∥ e 25 ∥ 2 + ∥ e 26 ∥ 2 ) (8-48) \frac{1}{2}\left(\left\|e_{11}\right\|^{2}+\left\|e_{12}\right\|^{2}+\left\|e_{13}\right\|^{2}+\left\|e_{14}\right\|^{2}+\left\|e_{23}\right\|^{2}+\left\|e_{24}\right\|^{2}+\left\|e_{25}\right\|^{2}+\left\|e_{26}\right\|^{2}\right) \tag{8-48} 21(∥e11∥2+∥e12∥2+∥e13∥2+∥e14∥2+∥e23∥2+∥e24∥2+∥e25∥2+∥e26∥2)(8-48)
令 J 11 \boldsymbol{J}_{11} J11 为 e 11 \boldsymbol{e}_{11} e11 对应的雅克比矩阵,且 e 11 \boldsymbol{e}_{11} e11 对其他相机变量和路标点的偏导都为零。我们把所有变量以 x = ( ξ 1 , ξ 2 , p 1 , ⋯ , p 6 ) T \boldsymbol{x}=\left(\boldsymbol{\xi}_{1}, \boldsymbol{\xi}_{2}, \boldsymbol{p}_{1}, \cdots, \boldsymbol{p}_{6}\right)^{\mathrm{T}} x=(ξ1,ξ2,p1,⋯,p6)T 的顺序摆放,则有
J 11 = ∂ e 11 ∂ x = ( ∂ e 11 ∂ ξ 1 , 0 2 × 6 , ∂ e 11 ∂ p 1 , 0 2 × 3 , 0 2 × 3 , 0 2 × 3 , 0 2 × 3 , 0 2 × 3 ) (8-49) \boldsymbol{J}_{11}=\frac{\partial \boldsymbol{e}_{11}}{\partial \boldsymbol{x}}=\left(\frac{\partial \boldsymbol{e}_{11}}{\partial \boldsymbol{\xi}_{1}}, \mathbf{0}_{2 \times 6}, \frac{\partial \boldsymbol{e}_{11}}{\partial \boldsymbol{p}_{1}}, \mathbf{0}_{2 \times 3}, \mathbf{0}_{2 \times 3}, \mathbf{0}_{2 \times 3}, \mathbf{0}_{2 \times 3}, \mathbf{0}_{2 \times 3}\right) \tag{8-49} J11=∂x∂e11=(∂ξ1∂e11,02×6,∂p1∂e11,02×3,02×3,02×3,02×3,02×3)(8-49)
我们用下图直观地表示雅克比矩阵的稀疏性:
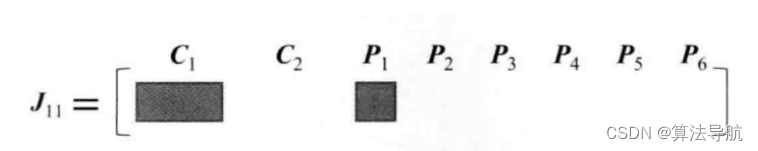
由此,可以得到整体雅克比矩阵 J \boldsymbol{J} J 和 H \boldsymbol{H} H矩阵。
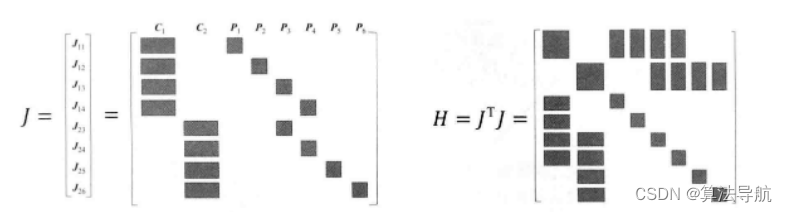
H \boldsymbol{H} H 矩阵中非对角部分的非零矩阵块(长方形块)可理解为其对应的两个变量之间的关系。
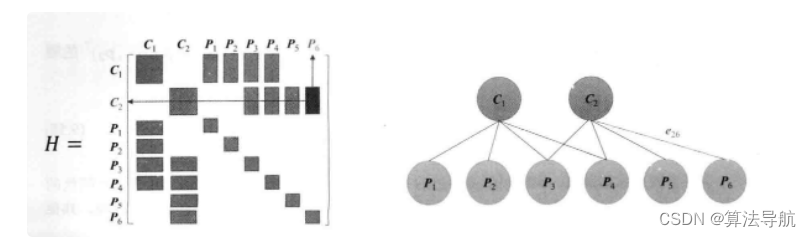
更一般地,假设有 m m m 个相机位姿, n n n个路标点,且通常路标点的数量远多于相机,即 n ≫ m n \gg m n≫m。这种情况下的 H \boldsymbol{H} H 矩阵如下图所示,左上角块非常小,右下对角块很大,由于形状很像箭头,又称为箭头形矩阵。
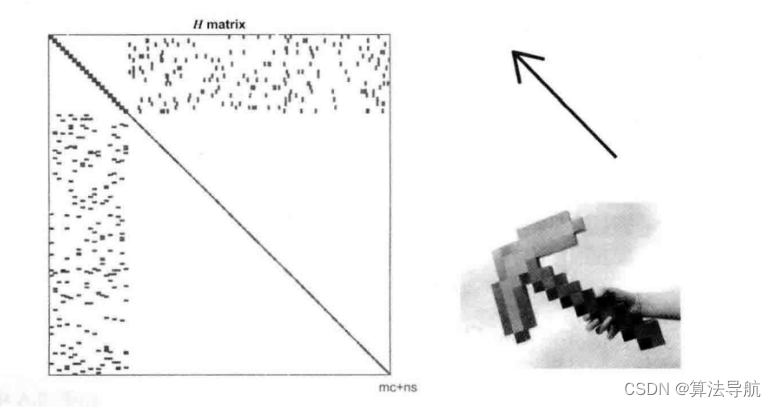
(4)将 H \boldsymbol{H} H 矩阵划分为四个区域,不难看出,左上角为对角块矩阵,且每个对角块元素的维度与相机位姿维度相同,同样的,右下角也是对角块矩阵,且每个对角块元素的维度与路标点维度相同。而且这四个区域和式(8-44)中的矩阵块是对应的。

那么,增量方程 H Δ x = g \boldsymbol{H} \Delta\boldsymbol{x}=\boldsymbol{g} HΔx=g 可写为以下形式
[ B E E T C ] [ Δ x c Δ x p ] = [ v w ] (8-50) \left[\begin{array}{cc} \boldsymbol{B} & \boldsymbol{E} \\ \boldsymbol{E}^{\mathrm{T}} & \boldsymbol{C} \end{array}\right]\left[\begin{array}{l} \Delta \boldsymbol{x}_{\mathrm{c}} \\ \Delta \boldsymbol{x}_{p} \end{array}\right]=\left[\begin{array}{l} \boldsymbol{v} \\ \boldsymbol{w} \end{array}\right] \tag{8-50} [BETEC][ΔxcΔxp]=[vw](8-50)
对角块矩阵求逆的难度远小于一般矩阵的求逆难度,所以只需要对对角块矩阵分别求逆即可。对线性方程组进行高斯消元,得
[ I − E C − 1 0 I ] [ B E E T C ] [ Δ x c Δ x p ] = [ I − E C − 1 0 I ] [ v w ] (8-51) \left[\begin{array}{cc} \boldsymbol{I} & -\boldsymbol{E} \boldsymbol{C}^{-1} \\ \mathbf{0} & \boldsymbol{I} \end{array}\right]\left[\begin{array}{cc} \boldsymbol{B} & \boldsymbol{E} \\ \boldsymbol{E}^{\mathrm{T}} & C \end{array}\right]\left[\begin{array}{l} \Delta \boldsymbol{x}_{\mathrm{c}} \\ \Delta \boldsymbol{x}_{p} \end{array}\right]=\left[\begin{array}{cc} \boldsymbol{I} & -\boldsymbol{E} \boldsymbol{C}^{-1} \\ 0 & \boldsymbol{I} \end{array}\right]\left[\begin{array}{l} \boldsymbol{v} \\ \boldsymbol{w} \end{array}\right] \tag{8-51} [I0−EC−1I][BETEC][ΔxcΔxp]=[I0−EC−1I][vw](8-51)
整理,得
[ B − E C − 1 E T 0 E T C ] [ Δ x c Δ x p ] = [ v − E C − 1 w w ] (8-52) \left[\begin{array}{cc} \boldsymbol{B}-\boldsymbol{E} \boldsymbol{C}^{-1}\boldsymbol{E}^{\mathrm{T}} & \boldsymbol{0} \\ \boldsymbol{E}^{\mathrm{T}} & \boldsymbol{C} \end{array}\right]\left[\begin{array}{l} \Delta \boldsymbol{x}_{\mathrm{c}} \\ \Delta \boldsymbol{x}_{p} \end{array}\right]=\left[\begin{array}{c} \boldsymbol{v}-\boldsymbol{E} \boldsymbol{C}^{-1} \boldsymbol{w} \\ \boldsymbol{w} \end{array}\right] \tag{8-52} [B−EC−1ETET0C][ΔxcΔxp]=[v−EC−1ww](8-52)
可以看出,方程第一行只和 Δ x c \Delta \boldsymbol{x}_c Δxc 有关,我们可以先将 Δ x c \Delta \boldsymbol{x}_c Δxc 解出来:
( B − E C − 1 E T ) Δ x c = v − E C − 1 w (8-53) (\boldsymbol{B}-\boldsymbol{E} \boldsymbol{C}^{-1}\boldsymbol{E}^{\mathrm{T}})\Delta \boldsymbol{x}_c=\boldsymbol{v}-\boldsymbol{E} \boldsymbol{C}^{-1} \boldsymbol{w} \tag{8-53} (B−EC−1ET)Δxc=v−EC−1w(8-53)
Δ x c \Delta \boldsymbol{x}_c Δxc 解出来后,再将其代入第二行方程,从而将 Δ x p \Delta \boldsymbol{x}_p Δxp 求解出来。这个过程称为 Schur (舒尔)消元。相较于直接求解的方法,它的优势在于:
① 消元过程中, C \boldsymbol{C} C 为对角块,故 C − 1 \boldsymbol{C}^{-1} C−1 容易求出;
② Δ x c \Delta \boldsymbol{x}_c Δxc 解出来后,根据 Δ x p = C − 1 ( w − E T Δ x c ) \Delta \boldsymbol{x}_{p}=\boldsymbol{C}^{-1}\left(\boldsymbol{w}-\boldsymbol{E}^{\mathrm{T}} \Delta \boldsymbol{x}_{\mathrm{c}}\right) Δxp=C−1(w−ETΔxc) 解出路标的增量方程。
(5)从概率角度来看,我们称这一步为 边缘化。我们将求解 ( Δ x c , Δ x p ) (\Delta \boldsymbol{x}_c,\Delta \boldsymbol{x}_p) (Δxc,Δxp) 的问题,转化成了先固定 Δ x p \Delta \boldsymbol{x}_p Δxp,求出 Δ x c \Delta \boldsymbol{x}_c Δxc,再求 Δ x p \Delta \boldsymbol{x}_p Δxp 的过程。这相当于做了条件概率展开:
P ( x c , x p ) = P ( x c ∣ x p ) P ( x p ) (8-54) P(\boldsymbol{x}_c,\boldsymbol{x}_p)=P( \boldsymbol{x}_c | \boldsymbol{x}_p)P(\boldsymbol{x}_p) \tag{8-54} P(xc,xp)=P(xc∣xp)P(xp)(8-54)
8.2.4 鲁棒核函数
在前面的 BA 问题中,我们将最小化误差项的二范数平方和作为目标函数,这样虽然直观,但是如果出现误匹配,该误差项会很大,从而将对整体函数产生较大影响,进而影响最终优化结果。
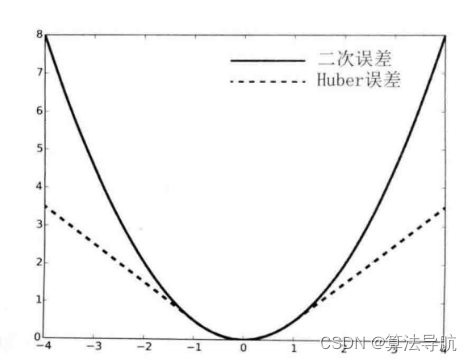
对此,我们将原先误差的二范数度量替换成一个增长没那么快的函数,同时保证光滑性质,使得优化结果更加稳健(减小误匹配项的影响),这样的函数称为 鲁棒核函数。鲁棒核函数有很多种,如 Huber 核:
H ( e ) = { 1 2 e 2 当 ∣ e ∣ ⩽ δ , δ ( ∣ e ∣ − 1 2 δ ) 其他 (8-55) H(e)= \begin{cases}\frac{1}{2} e^{2} & \text { 当 }|e| \leqslant \delta, \\ \delta\left(|e|-\frac{1}{2} \delta\right) & \text { 其他 }\end{cases} \tag{8-55} H(e)={21e2δ(∣e∣−21δ) 当 ∣e∣⩽δ, 其他 (8-55)
当误差
e
e
e 大于阈值
δ
\delta
δ 时,函数增长由二次形式转为一次形式,相当于限制了梯度的最大值。同时 Huber 核函数又是光滑的,可以很方便的求导。如下图,在误差较大时,Huber 核函数增长明显低于二次函数。