论文地址：[1406.2661] Generative Adversarial Networks (arxiv.org)

“GAN之父” Ian Goodfellow 发表的第一篇提出 GAN 的论文，这应该是任何开始研究学习 GAN 的都该阅读的一篇论文，它提出了 GAN 这个模型框架，讨论了非饱和的损失函数，然后对于最佳判别器(optimal discriminator)给出其导数，然后进行证明；最后是在 Mnist、TFD、CIFAR-10 数据集上进行了实验。

摘要：

生成器和判别器在训练过程中相互对抗，共同进化。

一个用来捕获数据分布的生成模型G，和一个用来估计样本来自训练数据而不是G的概率的判别模型D，G的训练过程是最大化D产生错误的概率。这个框架相当于一个极小化极大的双方博弈。在任意函数G和D的空间中唯一的解，其中G恢复训练分布，并且D处处都等于1/2.

研究背景：

最成功的模型之一就是判别式模型，通常他们将高维丰富的输入映射到类标签上。然而生成模型的发展并不乐观，由于最大似然估计和相关策略中出现的许多难以解决的概率计算的困难，以及难以利用在生成上下文中时使用分段线性单元的好处，深度生成模型的影响很小。

作者受到零和博弈的启发，在提出的对抗网络框架中，生成模型对抗着一个对手：一个学习去判别一个样本是来自模型分布还是数据分布的判别模型。生成模型可以被认定是一个伪造团队，试图产生假货并在不被发现的情况下使用它，而判别模型类似于监管/警察，试图检测假币。在这个游戏的竞争中驱使两个团队改进他们的方法，直到真假难分。

 

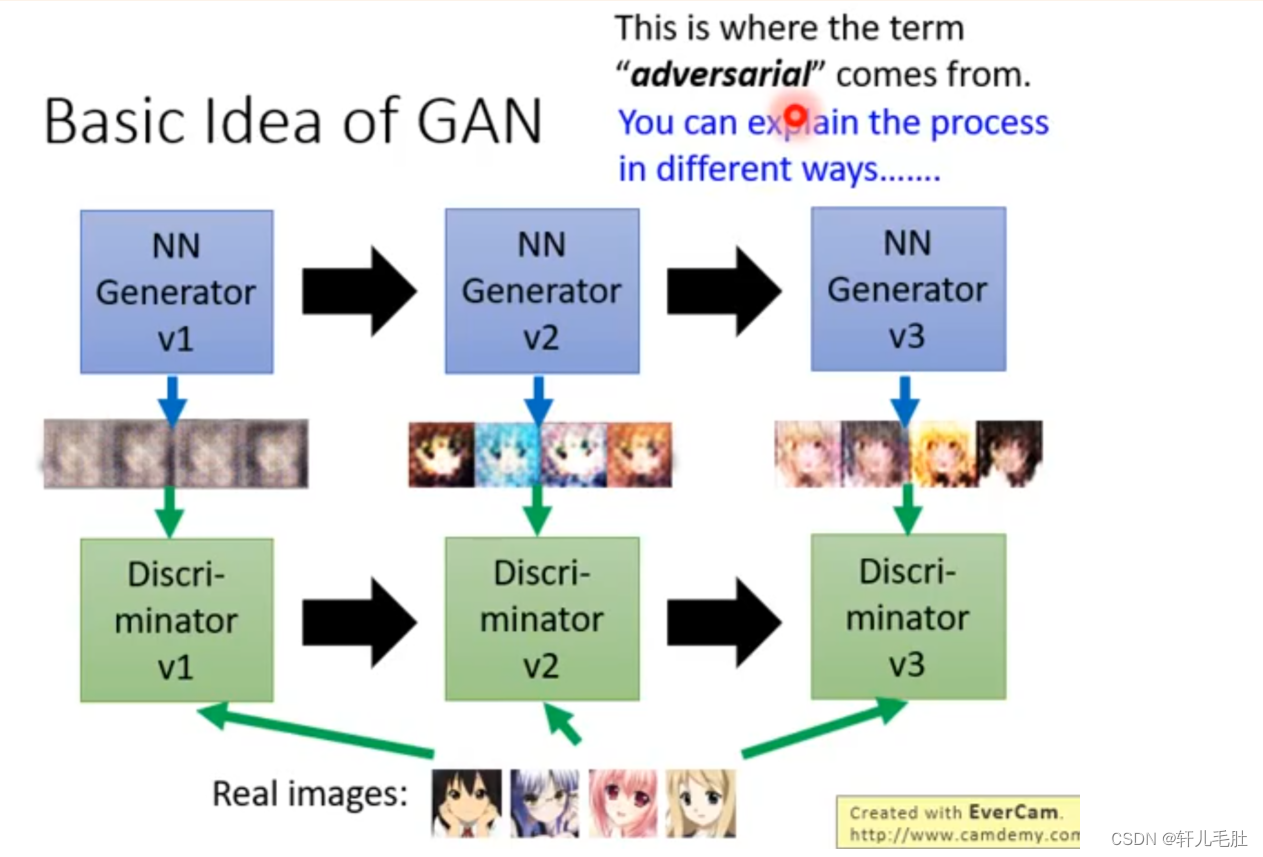
模型概述：

作者用MLP做基本网络层，去搭建判别器和生成器。

生成器G的定义：为了学习生成器关于数据上的分布𝑃𝑔，我们定义输入噪声的先验变量𝑃𝑧(𝑧)，然后使用G(z;𝜃𝑔)来代表数据空间的映射，G是一个由含有参数𝜃𝑔的多层感知机表示的可微函数。

G=argmin𝐺𝐷𝑖𝑣(𝑃𝐺,𝑃𝑑𝑎𝑡𝑎)

G的目标：将任意分布的数据输入和生成数据的分布近似。

判别器D的定义：定义一个多层感知机D(x;𝜃𝑑)用来输出一个单独的标量，这个标量可以理解成判别器对输入数据的打分，代表着输入数据来自于真实数据分布而不是生成数据的概率。

价值函数

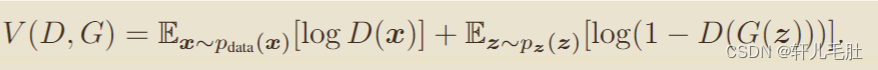
当G被给定的时候，

D=argmaxDV(D,G)

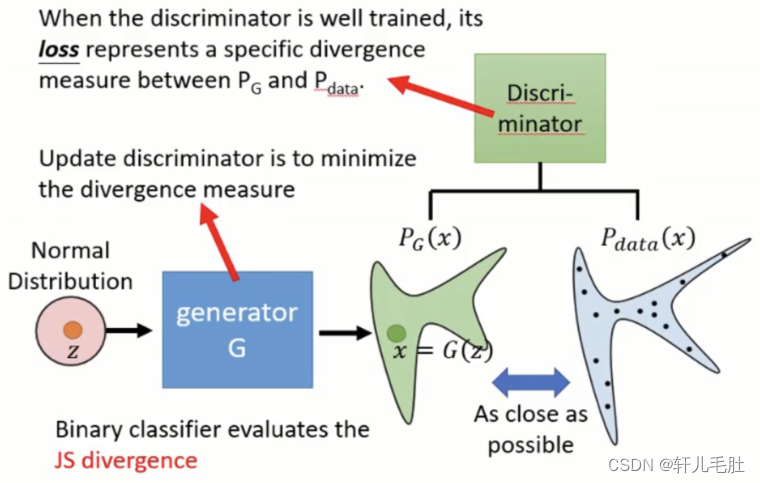
我们训练D来最大化分配正确标签给不管是来自于训练样例还是生成的样例的概率，同时我们训练G去最小化log(1-D(G(z)))

换句话说就是关键价值函数的两人博弈问题：

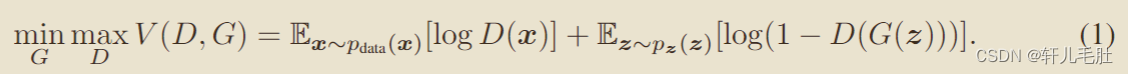
理论分析：

如何训练这个网络？

实际上，我们必须使用迭代数值方法来实现这个过程。在训练的内部循环中直接将D优化到头是不可行的，并且在有限的数据集上会导致过拟合。相反，我们在优化D的k个步骤和优化G的一个步骤之间交替进行。只要G变化足够慢，就可以保证D保持在接近其最优解的位置。

算法

理论分析：

优缺点：

缺点：主要是为𝑃𝑔(𝑥)没有明确的表示，可解释性差，且训练期间，生成器和判别器必须很好的同步（尤其是，不更新D时，G不必过度训练，为避免“Helvetica情景”）

优点：①根据实际结果。GAN的结果看上去可以比其他模型产生更好的样本②无需马尔可夫链，仅用反向传播就可以获得梯度，学习间无需推理，且模型中可融入多种函数

思考：

如何去评估模型的好坏？

生成器可以模拟任何数据分布？对input数据有什么样的要求？