今天开始讲图论
目录
图的存储
算任意两点的最短路径:
floyed算法:
算一个点到其他所有点的最短距离
dijkstra算法:
spfa算法:
图的存储
其实:邻接矩阵和链式向前星都能存边的信息,vector只能存点的信息,再搭配上v[]便可存点的权值,如果是树的话也建议vector)
邻接矩阵:(可存边信息)
邻接表:vector法(存点信息)(也可以搞一个fa[]存每个点父亲)链式向前星(存边信息)
下面是链式向前星的模板
#include <bits/stdc++.h>
using namespace std;
int tot,n,m;
int head[100];//存放每个点起边的标号
struct edge{
int to,w,next;//to是边终点,next是下一条边的标号(不用存起点,因为我们是通过起点来找边号的)
}e[100];//存储边,每条边都有唯一下标
void add(int u,int v,int w){
e[++tot].to=v; //这里我们一般从1开始存边,是因为head里面我们默认0时无边 !!!
e[tot].w=w;
e[tot].next=head[u]; head[u]=tot;//后来的边就插在最前面(这里有个细节:因为最开始head内容是0,所以最后一个边的next一定是0)
}
int main(){
int u,v,w;
cin>>n>>m; //n个点,m个边
for(int i=1;i<=m;i++){
cin>>u>>v>>w;
add(u,v,w);
}
for(int x=1;x<=n;x++){//把每个起点都遍历一遍
for(int i=head[x];i!=0;i=e[i].next){ //遍历每个点连的边i
cout<<x<<','<<e[i].to<<'\n';
}
}
}
算任意两点的最短路径:
floyed算法:
O(n^3) 可以处理负权图,不能判断负环图
思想:从第一个点开始,循环n次,依次加入每个点,看看因为这个点的加入,所有点间距离因此而变小就更新
int main(){ //floyed算法
int n;cin>>n;int w[n+1][n+1];
memset(w,0x3f,sizeof(w));//若是无向图,对角点初始化为0即可,有联系的点间放权值即可;对角点要初始化
for(int k=1;k<=n;k++)//依次放入每个点进行中转,这一层是可以单独拿出来的
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
if(w[i][j]>w[i][k]+w[k][j])//距离变短就更新
w[i][j]=w[i][k]+w[k][j];
}
}
算一个点到其他所有点的最短距离
spfa算法:O(nm)=O(KV) 可以处理负权图,判断负环图(负环就是一圈相加起来的权值是个负数)
思想:先将起点加入队列,每次从队列中取出一个点,遍历相邻边找到因该点加入而距离变小的点更新,更新成功的点重新入队,重复至队空
bellman-ford算法:
时间复杂度O(nm) 可以处理负权图,判断负环图
dijkstra算法:
O(n^2)或O(nlogn) 只能处理非负权图
思想:每次贪心地选出一个最小路径的点变成白点(确定点),遍历相邻边找到因该点加入而距离变小的点更新,重复至队空(白点自动会跳过)(如果出现负权,这会直接导致选白点的时候就出错了,因此就不能使用该算法)
题:

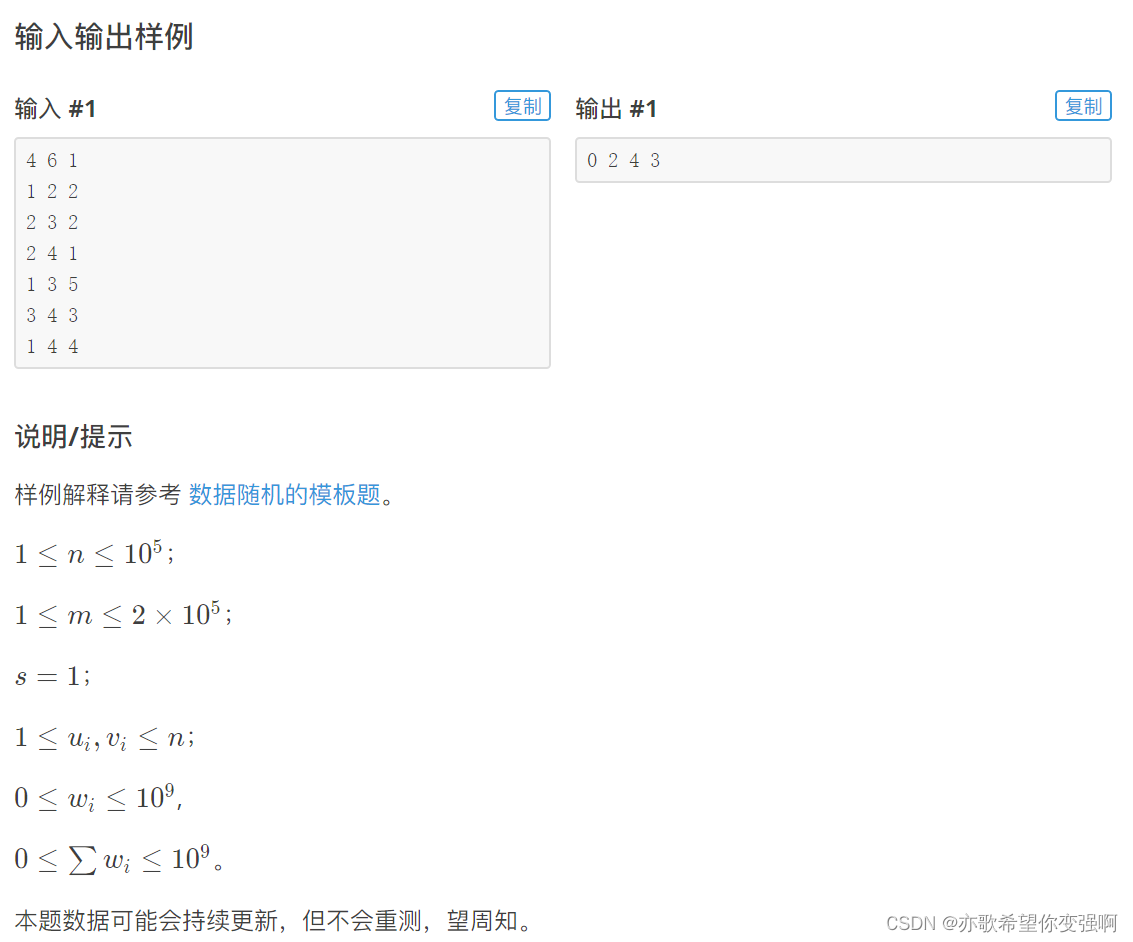
dijkstra算法:
(原理:贪心思想,确定白点的过程就是贪心,故不能处理负边权)
1. 初始化dis[s]=0,其余点dis为无穷大.
2. 取出队中dis值最小的蓝点cur,变成白点后遍历周围点v,当dis[cur]+w<dis[v],就更新dis[v] (若cur已为白点,就跳过,这点不同于spfa)
3,被更新的点入队,等待重新更新周围点
4,重复操作,直到队空,也就是所有点都变成了白点
(注意队列一些点的dis值会越来越多,分两种情况:(对蓝点)取出来的一定是可以变成白点的,不用管; (对白点)dis中值一定比队列中的小,我们跳过即可)
我们提供有两种判断办法:
第一种是对出队元素pos的dis和dis[cur]比较,若不相等则说明选出旧白点了,就跳过
第二种方法是对已经成为白点的进行标记,若出队元素早已经是白点了,就跳过
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> pa; //pair中first是距离,second是起点到的它点
const int N=1e5+10,M=2e5+10;
int n,m,s,t,tot;
int pre[N];
int head[N],dis[N],vis[N]; //head[i]存放起点i周围的边号,vis标记此点是否为白点(即已确定的点)
struct edge {int to,w,next; } e[M];//如果N,M没有const修饰,这里要报错的
priority_queue<pa,vector<pa>,greater<pa>> Q; //小根堆,按dis升序排列
void add(int u,int v,int w) {e[++tot]=(edge){v,w,head[u]};head[u]=tot;}
void dijkstra(int s) {
memset(dis,0x3f,sizeof(dis));dis[s]=0;
Q.push(make_pair(0,s)); //make_pair函数的返回值是一个pair,功能是将两个数据合成一个pair
while (!Q.empty()) {
int cur=Q.top().second;Q.pop();//出队就相当于取出最小蓝点
if (vis[cur]) continue;//跳过旧白点
vis[cur]=1;
for (int i=head[cur];i;i=e[i].next) { //i为边号 遍历cur连向周围所有边i的点v
int v=e[i].to,w=e[i].w;
if (dis[cur]+w<dis[v]) dis[v]=dis[cur]+w,Q.push(make_pair(dis[v],v));//更新后就要入队,等待重新更新周围点
}
}
}
int main() {
cin>>n>>m>>s;int u,v,w;
for (int i=1;i<=m;++i) {
cin>>u>>v>>w;
add(u,v,w);
}
dijkstra(s);
for (int i=1;i<=n;++i) cout<<dis[i]<<' ';
return 0;
}
//另一个判断方式+具体路径输出
void print(int u){
if(u==0)return;
print(pre[u]);
cout<<u<<"->";
}
void dijkstra(int s) {
memset(dis,0x3f,sizeof(dis));dis[s]=0;
Q.push(make_pair(0,s));
while (!Q.empty()) {
int pos=Q.top().second,dis_=Q.top().first; Q.pop();
if (dis_!=dis[pos]) continue;//跳过旧白点
for (int i=head[pos];i;i=e[i].next) {
int to=e[i].to,w=e[i].w;
if (dis[pos]+w<dis[to]) dis[to]=dis[pos]+w,pre[v]=cur,Q.push(make_pair(dis[to],to));
}
}
}
main:
for (int i=1;i<=n;++i) {
cout<<dis[i]<<": ";
print(i);cout<<'\n';
}
spfa算法步骤:
(原理就是线性dp,由以确定点按拓扑序推下个未确定点,然后未确定点由前面多个以确定点决策,就是按层递推)
1. 初始化dis[s]=0,其余dis为无穷大(vis[s]=1)
2,cur出队,遍历周围点v,当dis[cur]+w<dis[v],就更新dis[v](vis[cur]=0)
3,(松弛,入队)被更新的且不在队伍的点入队,等待重新更新周围点(vis[v]=1)(这一步与dijkstra不同,因为已经入过队的可能还会入队,故可处理负边权)
4,重复操作,直到队空
不过此题卡spfa,但是因为还是要给出来,因为spfa算法可用地方太多了,比如spfa还可以处理最长路问题
#include <bits/stdc++.h>
using namespace std;
const int N=1e4, M=1e4;
int head[N],vis[N],dis[N],tot,n,m;//head是表头(head[i]表示i起点的边号),vis表示该点是否已在队列中,为了防止同个点重复入队
struct node{int to,w,next;} e[M];
void add(int u,int v,int w){e[++tot]=(node){v,w,head[u]};head[u]=tot;}
void spfa(int t){
queue<int> q;
memset(dis,0x3f,sizeof(dis));
dis[t]=0; vis[t]=1; //注意vis等于1表示队列中已经存在此点
q.push(t);
while(!q.empty()){
int cur=q.front(); q.pop();
vis[cur]=0;//扩展后此点出队
for(int i=head[cur];i;i=e[i].next){//i是边号 遍历点cur连向的周围边i的点v
int v=e[i].to,w=e[i].w;
if(dis[v]>dis[cur]+w){//判断是否需要更新,更新过的且不在队伍的点才入队,方便找更优解
dis[v]=dis[cur]+w;
if(!vis[v])q.push(v),vis[v]=1;
}
}
}
}
int main(){
int n,m,t;
cin>>n>>m>>t;
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
add(u,v,w);
}
spfa(t);
for(int i=1;i<=n;i++){
cout<<dis[i]<<" ";
}
return 0;
}
题目:我们把上百件衣服从商店运回赛场,求最短的从上商店到赛场的路线
输入:第一行N(<=100),M(<=10000),N表示有几个路口(1号路口是商场所在地,n号是赛场)M表示有几条路,N=M=0时输入结束,接下来M行每行包括A,B,C表示A,B两口路需要耗时C时间
输出:对每组输入,输出一行,表示工作人员从商店到赛场的最短时间
样例: 2 1 输出:3
1 2 3 2
3 3
1 2 5
2 3 5
3 1 2
0 0
#include <bits/stdc++.h>
using namespace std;
const int N=1e4+10;
const int M=1e4+10;
long long dis[N],u[N],v[N],w[N];//按边初始化无向图
int n,m,cnt;
long long ans;
long long bellman_fold(int s,int t){
memset(dis,0x3f,sizeof(dis));//初始化无穷大
dis[s]=0;
for(int i=1;i<=n-1;i++){//最多松弛n-1次
int check=0;//是否可以提前结束松弛
for(int j=1;j<=cnt;j++){//对每条边进行松弛,更新dis
if(dis[u[j]]+w[j]<dis[v[j]]){
dis[v[j]]=dis[u[j]]+w[j];
check=1;
}
}
if(check==0)break;
}
return dis[t];
}
int main(){
while((cin>>n>>m)&&(n+m)){
cnt=1;
for(int i=1;i<=m;i++){//初始化无向图(按边),因为只需要用到每条边,所有初始化只需要按边初始化即可
int x,y,z;
cin>>x>>y>>z;
u[cnt]=x;v[cnt]=y;w[cnt]=z;//w表示每条边的长度,u表示对应边的起点,v表示对边的终点,这样方便对每条边访问
cnt++;
u[cnt]=y;v[cnt]=x;w[cnt]=z;
cnt++;
}
ans=bellman_fold(1,n);
cout<<ans<<endl;
}
}不过bellman我不怎么用,只是给出来一下。