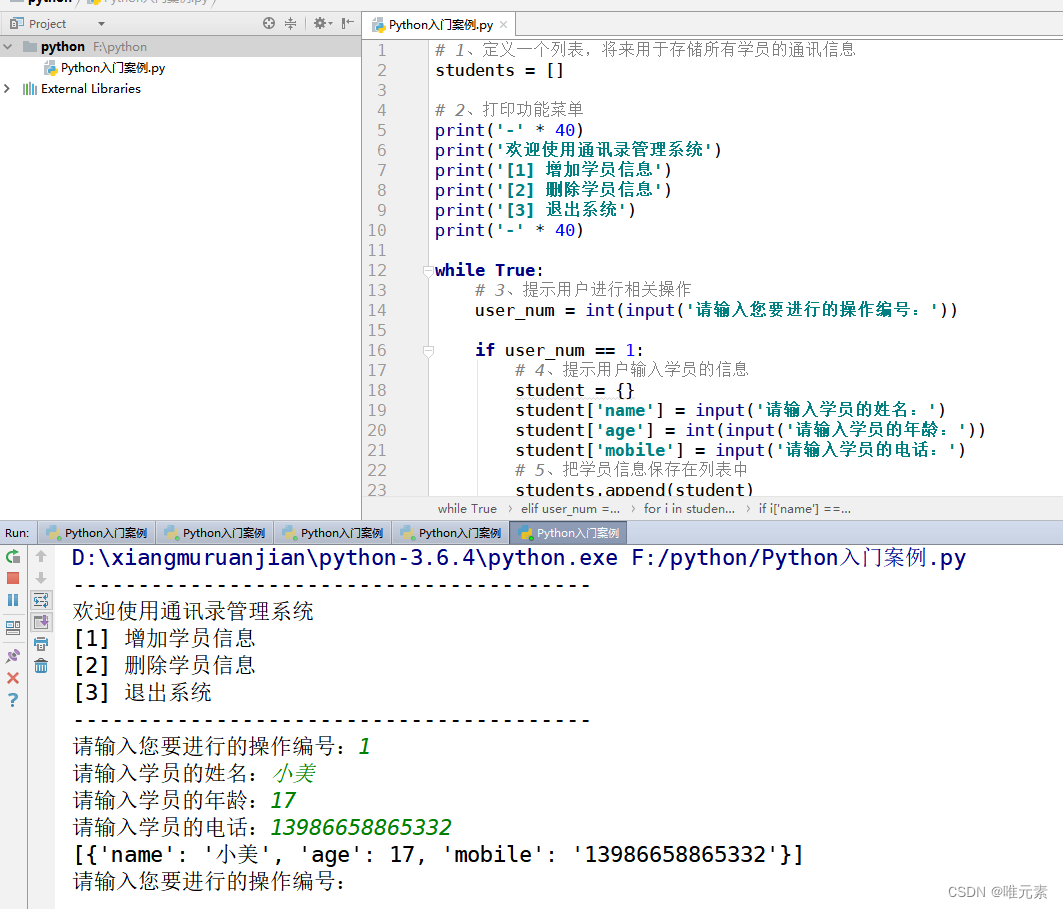
本博客参考算法（第4版）：算法（第4版） - LeetBook - 力扣（LeetCode）全球极客挚爱的技术成长平台

本文用Java实现相关算法。

我们关注的主要对象是重新排列数组元素的算法，其中每个元素都有一个主键。排序算法的目标就是将所有元素的主键按照某种方式排列（通常是按照大小或是字母顺序）。排序后索引较大的主键大于等于索引较小的主键。元素和主键的具体性质在不同的应用中千差万别。在 Java 中，元素通常都是对象，对主键的抽象描述则是通过一种内置的机制，如Comparable接口。

大多数情况下，我们的排序代码只会通过两个方法操作数据：less() 方法对元素进行比较，exch() 方法将元素交换位置。exch() 方法的实现很简单，通过 Comparable 接口实现 less() 方法也不困难。将数据操作限制在这两个方法中使得代码的可读性和可移植性更好，更容易验证代码的正确性、分析性能以及排序算法之间的比较。

在本文主键全是整数，因此不做接口实现，直接实现相关函数。

private static void exch(int[] arr, int i, int j) {
    int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp;
}
private static boolean less(int pre, int suf) {
    return pre < suf;
}

排序默认从小到大升序

初级排序算法

选择排序

一种最简单的排序算法是这样的：首先，找到数组中最小的那个元素，其次，将它和数组的第一个元素交换位置（如果第一个元素就是最小元素那么它就和自己交换）。再次，在剩下的元素中找到最小的元素，将它与数组的第二个元素交换位置。如此往复，直到将整个数组排序。这种方法叫做选择排序，因为它在不断地选择剩余元素之中的最小者。

代码实现：

public class lab {
    private static void exch(int[] arr, int i, int j) {
        int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp;
    }
    private static boolean less(int pre, int suf) {
        return pre < suf;
    }
    public static void sort(int[] arr) {
        int N = arr.length; // 数组长度
        for(int i = 0; i < N; ++i) {
            int pos = i; // 最小元素下标
            for(int j = i + 1; j < N; ++j) {
                // 如果有比当前最小元素a[j]小的，则更新最小元素下标
                if(less(arr[j], arr[pos])) pos = j;
            }
            // 交换当前位置i 和最小元素下标
            exch(arr, i, pos);
        }
    }
    public static int[] a = {5, 4, 1, 56, 3};
    // 测试
    public static void main(String[] args) {
        sort(a);
        for(int i : a) System.out.println(i);
    }
}

交换元素的代码写在内循环之外，每次交换都能排定一个元素，因此交换的总次数是 N。所以算法的时间效率取决于比较的次数。

对于长度为 N 的数组，选择排序需要大约 N^2/2 次比较和N次交换。

选择排序两个鲜明的特点：

• 运行时间和输入无关
• 数据移动是最少的

插入排序

通常人们整理桥牌的方法是一张一张的来，将每一张牌插入到其他已经有序的牌中的适当位置。在计算机的实现中，为了给要插入的元素腾出空间，我们需要将其余所有元素在插入之前都向右移动一位。这种算法叫做插入排序。

和选择排序不同的是，插入排序所需的时间取决于输入中元素的初始顺序。例如，对一个很大且其中的元素已经有序（或接近有序）的数组进行排序将会比对随机顺序的数组或是逆序数组进行排序要快得多。

代码实现：

public class lab {
    private static void exch(int[] arr, int i, int j) {
        int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp;
    }
    private static boolean less(int pre, int suf) {
        return pre < suf;
    }
    public static void sort(int[] arr) {
        int N = arr.length; // 数组长度
        for(int i = 1; i < N; ++i) {
            // 将 a[i] 插入到 a[i-1]、a[i-2]、a[i-3]...之中
            for(int j = i; j > 0 && less(a[j], a[j - 1]); --j) {
                exch(arr, j, j - 1);
            }
        }
    }
    public static int[] a = {5, 4, 1, 56, 3};
    // 测试
    public static void main(String[] args) {
        sort(a);
        for(int i : a) System.out.println(i);
    }
}

对于随机排序的长度N且主键不重复的数组，平均情况下插入需要N * N / 4次比较及N * N / 4次交换。最坏是N * N / 2次比较和交换。最好情况是N - 1次比较和0次交换（已有序数组）。

插入排序对部分有序的数组很有效果，例如：

• 数组中每个元素距离它的最终位置都不远；
• 一个有序的大数组接一个小数组；
• 数组中只有几个元素的位置不正确。

插入排序需要的交换操作和数组中倒置的数量相同，需要的比较次数大于等于倒置的数量，小于等于倒置的数量加上数组的大小再减一。

希尔排序

优化插入排序。希尔排序为了加快速度简单地改进了插入排序，交换不相邻的元素以对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。

希尔排序的思想是使数组中任意间隔为 h 的元素都是有序的。这样的数组被称为 h 有序数组。对于任意以 1 结尾的 h 序列，我们都能够将数组排序，这就是希尔排序。

实现希尔排序的一种方法是对于每个 h，用插入排序将 h 个子数组独立地排序。但因为子数组是相互独立的，一个更简单的方法是在 h- 子数组中将每个元素交换到比它大的元素之前去（将比它大的元素向右移动一格）。只需要在插入排序的代码中将移动元素的距离由 1 改为 h 即可。这样，希尔排序的实现就转化为了一个类似于插入排序但使用不同增量的过程。

public class lab {
    private static void exch(int[] arr, int i, int j) {
        int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp;
    }
    private static boolean less(int pre, int suf) {
        return pre < suf;
    }
    public static void sort(int[] arr) {
        int N = arr.length; // 数组长度
        int h = 1;
        while(h < N / 3) h = 3 * h + 1; //  // 1, 4, 13, 40, 121, 364, 1093, ... 这样效果更优
        while(h >= 1) {
            // 虽然是两个for循环，但是加在一起是O(N)
            for(int i = h; i < N; ++i) {
                // 插入思想
                for(int j = i; j >= h && less(a[j], a[j - h]); j -= h) {
                    exch(arr, j, j - h);
                }
            }
            h /= 3;
        }
    }
    public static int[] a = {5, 4, 1, 56, 3};
    // 测试
    public static void main(String[] args) {
        sort(a);
        for(int i : a) System.out.println(i);
    }
}

归并排序

归并排序，可以先（递归地）将它分成两半分别排序，然后将结果归并起来。归并排序有原地归并、自顶向下、自顶向上这几种方法，本文只讲自顶向下的方法。

public class lab {
    private static void exch(int[] arr, int i, int j) {
        int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp;
    }
    private static boolean less(int pre, int suf) {
        return pre < suf;
    }
    public static void sort(int[] arr, int lo, int hi) {
        if(lo >= hi) return ;
        int mid = (lo + hi) / 2;
        // 将数组分为两部分，并对这两部分进行排序
        sort(arr, lo, mid); sort(arr, mid + 1, hi);
        merge(arr, lo, mid, hi);
    }
    // 将两个有序数组进行合并
    public static void merge(int[] arr, int lo, int mid, int hi) {
        int i = lo, j = mid + 1, k = 0;
        while(i <= mid && j <= hi) {
            if(less(arr[i], arr[j])) tmp[k++] = arr[i++];
            else tmp[k++] = arr[j++];
        }
        while(i <= mid) tmp[k++] = arr[i++];
        while(j <= hi) tmp[k++] = arr[j++];
        for(i = lo, k = 0; i <= hi; ++i, ++k) arr[i] = tmp[k];
    }
    public static int[] a = {5, 4, 1, 56, 3};
    public static int[] tmp = new int[5]; // 辅助数组
    // 测试
    public static void main(String[] args) {
        sort(a, 0, 4);
        for(int i : a) System.out.println(i);
    }
}

该算法需要N * lg(N) / 2到 N * lg(N)次比较。最多访问数组6 * N * lg(N)次。

快速排序

快速排序可能是应用最广泛的排序算法了。快速排序流行的原因是它实现简单、适用于各种不同的输入数据且在一般应用中比其他排序算法都要快得多。快速排序引人注目的特点包括它是原地排序（只需要一个很小的辅助栈）。

快速排序是一种分治的排序算法。它将一个数组分成两个子数组，将两部分独立地排序。**快速排序和归并排序是互补的：归并排序将数组分成两个子数组分别排序，并将有序的子数组归并以将整个数组排序；而快速排序将数组排序的方式则是当两个子数组都有序时整个数组也就自然有序了。**归并排序的递归调用发生在处理整个数组之前；快速排序是递归调用发生在处理整个数组之和。

public class lab {
    private static void exch(int[] arr, int i, int j) {
        int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp;
    }
    private static boolean less(int pre, int suf) {
        return pre < suf;
    }
    public static void sort(int[] arr, int lo, int hi) {
        if(lo >= hi) return ;
        // 进行切分，下标为partidx的元素在整个数组中是已经排序好的
        int partidx = partition(arr, lo, hi);
        // 对左右两部分进行排序
        sort(arr, lo, partidx - 1); sort(arr, partidx + 1, hi);
    }
    // 得到第j位是有序的对于整个数组来说
    public static int partition(int[] arr, int lo, int hi) {
        int i = lo, j = hi + 1; // 左右指针
        int v = arr[lo]; // 切分元素的值
        while(true) {
            // 扫描左右，检查扫描是否结束并交换元素
            while(less(arr[++i], v)) if(i == hi) break;
            while(less(v, arr[--j])) if(j == lo) break;
            if(i >= j) break;
            exch(arr, i, j);
        }
        exch(arr, lo, j);
        // 将这个数组第j位最终态找到
        return j;
    }
    public static int[] a = {5, 4, 1, 56, 3};
    public static int[] tmp = new int[5]; // 辅助数组
    // 测试
    public static void main(String[] args) {
        sort(a, 0, 4);
        for(int i : a) System.out.println(i);
    }
}

优先队列

优先队列是一种数据结构：支持快速的删除最大元素和插入元素。

优先队列可以用二叉堆实现。二叉堆，本质上是一种完全二叉树。

分类：二叉堆分为最大堆和最小堆两种类型，最大堆和最小堆分别又可称为大顶堆和小顶堆。最大堆中，任何一个父节点的值都大于或等于它的左、右孩子节点的值；最小堆中，任何一个父节点的值都小于或等于它的左、右孩子节点的值。

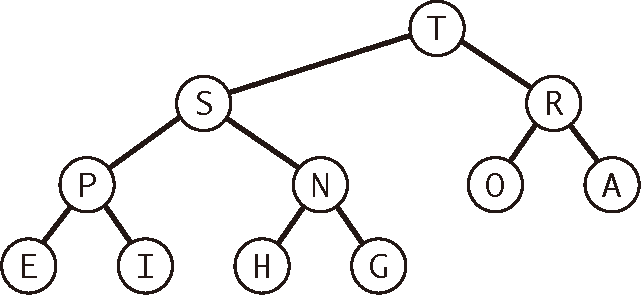
用数组（堆）实现的完全二叉树的结构是很严格的，但它的灵活性已经足以让我们高效地实现优先队列。用它们我们将能实现对数级别的插入元素和删除最大元素的操作。利用在数组中无需指针即可沿树上下移动的便利和以下性质，算法保证了对数复杂度的性能。

在有序化的过程中我们会遇到两种情况。当某个结点的优先级上升（或是在堆底加入一个新的元素）时，我们需要由下至上恢复堆的顺序。当某个结点的优先级下降（例如，将根结点替换为一个较小的元素）时，我们需要由上至下恢复堆的顺序。首先，我们会学习如何实现这两种辅助操作，然后再用它们实现插入元素和删除最大元素的操作。

由下向上的堆有序（上浮）

如果堆的有序状态因为某个结点变得比它的父结点更大而被打破，那么我们就需要通过交换它和它的父结点来修复堆。交换后，这个结点比它的两个子结点都大（一个是曾经的父结点，另一个比它更小，因为它是曾经父结点的子结点），但这个结点仍然可能比它现在的父结点更大。我们可以一遍遍地用同样的办法恢复秩序，将这个结点不断向上移动直到我们遇到了一个更大的父结点。

private void swim(int k)
{
   while (k > 1 && less(k/2, k))
   {
      exch(k/2, k);
      k /= 2;
   }
}

由上到下的堆有序（下沉）

private void sink(int k) {
    while(2 * k <= N) {
        int j = 2 * k;
        if(j < N && less(j, j + 1)) ++j;
        if(!less(k, j)) break;
        exch(k, j);
        k = j;
    }
}

堆排序

public class lab {
    private static void exch(int i, int j) {
        int temp = a[i]; a[i] = a[j]; a[j] = temp;
    }
    private static boolean less(int i, int j) {
        return a[i] < a[j];
    }
    public static void sort() {
        int N = a.length - 1;
        for(int k = N / 2; k >= 1; --k) {
            sink(k, N);
        }
        while(N > 1) {
            exch(1, N--);
            sink(1, N);
        }
    }
    private static void swim(int k) {
        while(k > 1 && less(a[k / 2], a[k])) {
            exch(k / 2, k);
            k /= 2;
        }
    }
    private static void sink(int k, int N) {
        while(2 * k <= N) {
            int j = 2 * k;
            if(j < N && less(j, j + 1)) ++j;
            if(!less(k, j)) break;
            exch(k, j);
            k = j;
        }
    }
    public static int[] a = {0, 5, 4, 1, 56, 3};
    // 测试
    public static void main(String[] args) {
        sort();
        for(int i : a) System.out.println(i);
    }
}

排序算法的时间复杂度和稳定性

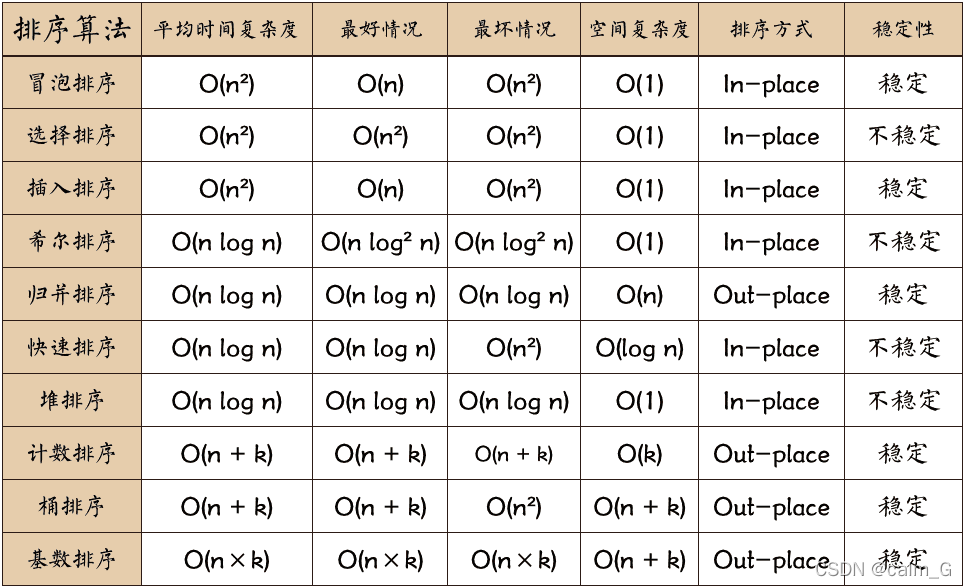
算法（第4版） - LeetBook - 力扣（LeetCode）全球极客挚爱的技术成长平台

二叉堆的节点插入、删除以及构建过程_二叉堆插入-CSDN博客

常用十大排序算法-CSDN博客