目录

介绍： 

代码：

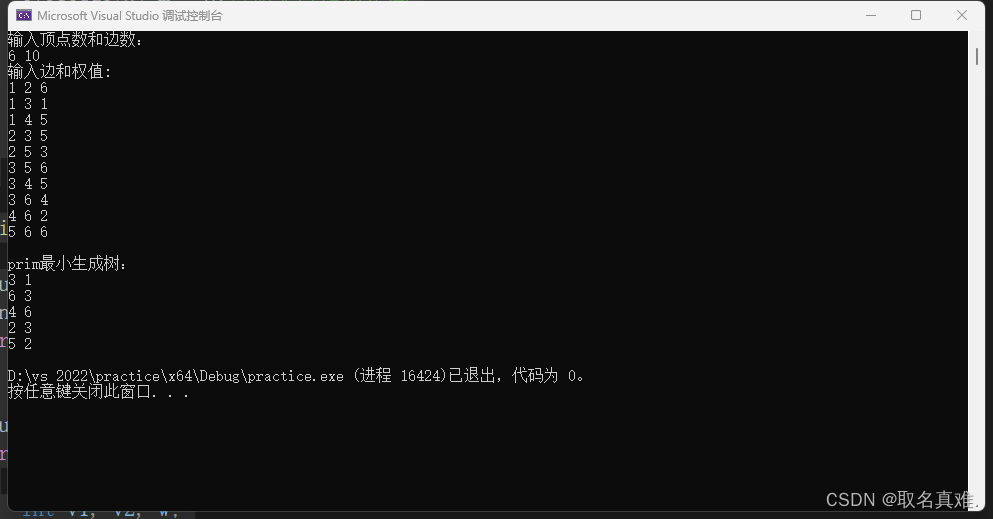
结果： 

介绍： 

   Prim算法是一种用于解决最小生成树问题的贪心算法。该算法的主要思想是从一个顶点开始，不断向图中添加边，直到构成一棵包含所有顶点的生成树，使得树的边权之和最小。

具体来说，Prim算法的过程如下：

1. 选择一个起始点，将其加入生成树中。

2. 若生成树中已经包含所有顶点，则算法结束；否则，从与生成树相邻的所有边中选择一条边权最小的边，将其加入生成树中。

3. 重复步骤2，直到生成树包含所有顶点。

需要注意的是，Prim算法要求构成的图必须是连通的。若原图不连通，则需要对每个连通分量分别运行Prim算法。此外，Prim算法的时间复杂度为O(E*logV)，其中E为边数，V为顶点数。

代码：

#include<iostream>
#include<vector>
using namespace std;
typedef struct node
{
	int adjvex;//与之相连最小权值边的另一顶点
	int w;//权值
}node;
int g [100][100];
int n, e;
node closedge[100];
void prim(int u)
{
	for (int i = 1; i <= n; i++)
		if (i != u)
			closedge[i] = { u, g[u][i] };//初始化closedge
	closedge[u].w = 0;//为零表示已经访问过，加入已访问集合
	for (int j = 1; j < n; j++)
	{
		int min = 999;
		int v;
		for (int i = 1; i <= n; i++)//找closedge中权值最小的边
		{
			if (closedge[i].w != 0 && closedge[i].w < min)
			{
				min = closedge[i].w;
				u = i;
			}
		}
		v = closedge[u].adjvex;
		cout << u << " " << v << endl;//输出权值最小的边
		closedge[u].w = 0;//加入已访问集合
		for (int i = 1; i <= n; i++)//加入新顶点后，更新closedge
		{
			if (g[u][i] < closedge[i].w)
				closedge[i] = { u,g[u][i] };
		}
	}
}
int main()
{
	cout << "输入顶点数和边数：" << endl;
	cin >> n >> e;
	for (int i = 1; i <= n; i++)//初始化矩阵
		for (int j = 1; j <= n; j++)
			g[i][j] = 999;
	cout << "输入边和权值:" << endl;
	for (int i = 0; i < e; i++)
	{
		int v1, v2, w;
		cin >> v1 >> v2>>w;
		g[v1][v2] = w;
		g[v2][v1] = w;//无向图
	}
	cout << endl;
	cout << "prim最小生成树：" << endl;
	prim(1);//从1点开始
}

结果：