矩阵置零00

news2024/11/17 11:41:37

题目链接

矩阵置零

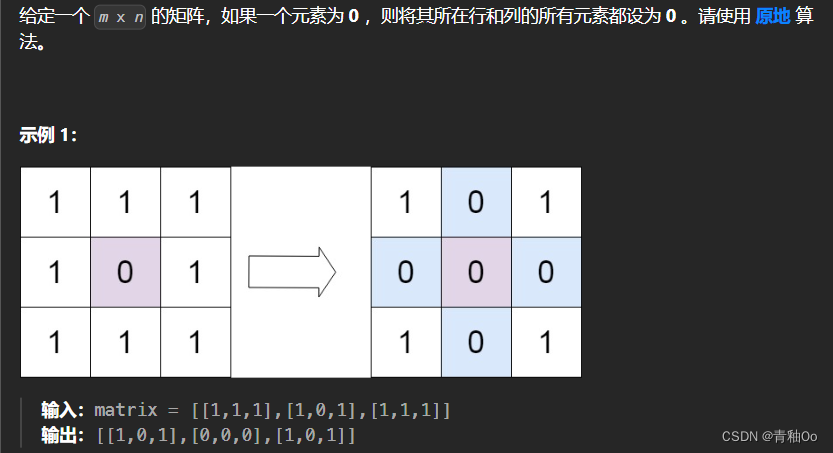
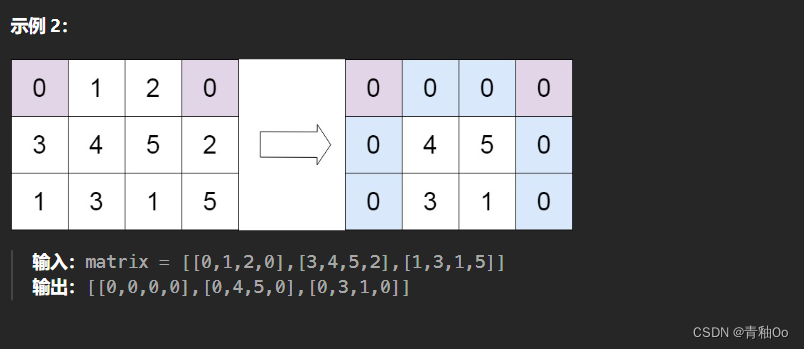
题目描述

注意点

使用原地算法

解答思路

思路是需要存储每一行以及每一列是否有0，因为要尽可能使用更少的空间，且新设置为0的格子不能对后续的判断产生影响，所以要在原有矩阵上存储该信息
先用两个参数存储第一行和第一列是否有0，再用第一行和第一列分别存储相应列和相应行中是否有0，也就是matrix[i][0]存储第i行是否有0，matrix[0][j]存储第j列是否有0，这样做相当于只用了2个额外空间，后续再根据matrix[i][0]和matrix[0][j]的信息更新matrix[i][j]的值，最后再更新第一行和第一列的值即可

代码

class Solution {
    public void setZeroes(int[][] matrix) {
        int row = matrix.length;
        int col = matrix[0].length;
        // 存储第一行和第一列是否有0
        int flag_row = 0;
        int flag_col = 0;
        while (flag_row < row && matrix[flag_row][0] != 0) {
            flag_row++;
        }
        while (flag_col < col && matrix[0][flag_col] != 0) {
            flag_col++;
        }
        // 第一行存储每一列是否有0，第一列分别存储每一行是否有0
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (flag_row != row) {
            for (int i = 0; i < row; i++) {
                matrix[i][0] = 0;
            }
        }
        if (flag_col != col) {
            for (int j = 0; j < col; j++) {
                matrix[0][j] = 0;
            }
        }
    }
}