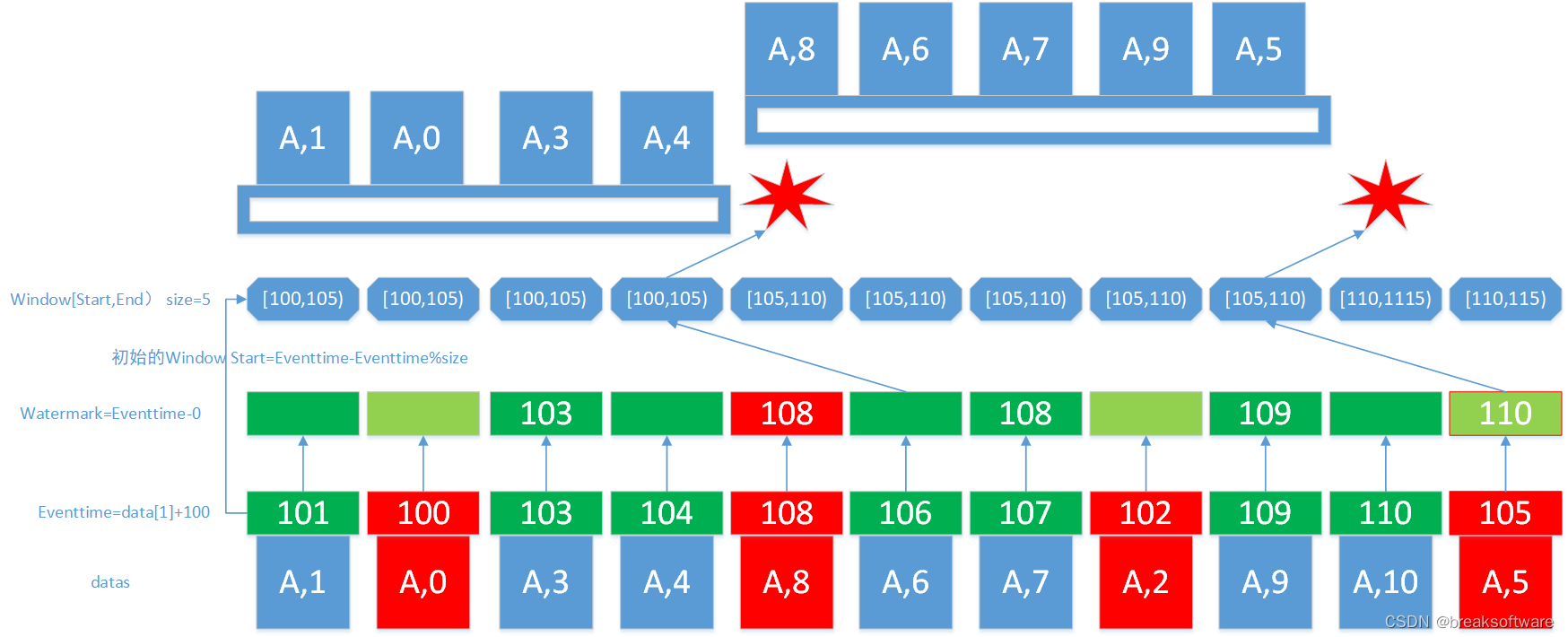
二叉排序树(BST)
二叉排序树,又称二叉查找树(BST,Binary Search Tree)
一颗二叉树或者是空二叉树,或者是具有如下性质的二叉树:
左子树上所有结点的关键字均小于根结点的关键字;
右子树上所有结点的关键字均大于根结点的关键字;
左子树和右子树又各是一颗二叉排序树
左子树结点值<根结点值<右子树结点值
进行中序遍历,可以得到一个递增的有序序列
二叉排序树的查找
BSTNode *BST_Search(BSTree T,int key){
while(T!=NULL&&key!=T->key){ //若树空或等于根结点值,则结束循环
if(key<T->key) T=T->lchild; //小于,则在左子树上查找
else T=T->rchild; //大于,则在右子树上查找
}
return T;
}
//在二叉排序树中查找值为key的结点(递归实现)
BSTNode *BSTSearch(BSTree T,int key){
if(T==NULL)
return NULL;//查找失败
if(key==T->key)
return T;//查找成功
else if(key<T->key)
return BSTSearch(T->lchild,key);//在左子树中找
else
return BSTSearch(T->rchild,key);//在右子树中找
}
二叉排序树的插入
若原二叉排序树为空,则直接插入结点;否则,若关键字k小于根结点值,则插入到左子树,若关键字k大于根结点值,则插入到右子树
//在二叉排序树插入关键字为k的新结点(递归实现)
int BST_Insert(BSTree &T,int k){
if(T==NULL){ //原树为空,新插入的结点为根结点
T=(BSTree)malloc(sizeof(BSTNode));
T->key=k;
T->lchild=T->rchild=NULL;
retunr 1; //返回1,插入成功
}
else if(k==T->key) //树中存在相同关键字的结点,插入失败
return 0;
else if(k<T->key) //插入到T的左子树
return BST_Insert(T->lchild,k);
else //插入到T的右子树
return BST_Insert(T->rchild,k);
}
二叉排序树的删除
先搜索找到目标结点:
1、若被删除结点z是叶结点,则直接删除,不会破坏二叉排序树的性质。
2、若结点z只有一棵左子树或右子树,则让z的子树成为z父结点的子树,替代z的位置。
3、若结点z有左、右两棵子树,则令z的直接后继(或直接前驱)替代z,然后从二叉排序树中删去这个直接后继(或直接前驱),这样就转换成了第一或第二种情况。
z的后继:z的右子树中最左下结点(该节点一定没有左子树)
z的前驱:z的左子树中最右下结点(该节点一定没有右子树)
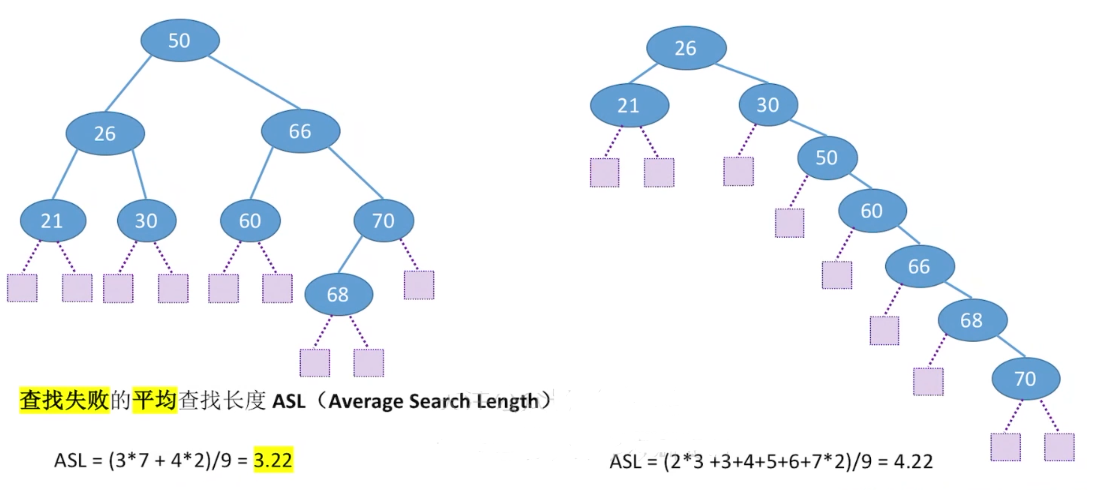
查找效率分析
查找长度–在查找运算中,需要对比关键字的次数称为查找长度,反映了查找操作时间复杂度

平衡二叉树
平衡二叉树(Balanced Binary Tree),简称平衡树(AVL树)–树上任一结点的左子树和右子树的高度之差不超过1。
结点的平衡因子=左子树高-右子树高
平衡二叉树的插入
每次调整的对象都是“最小不平衡子树”
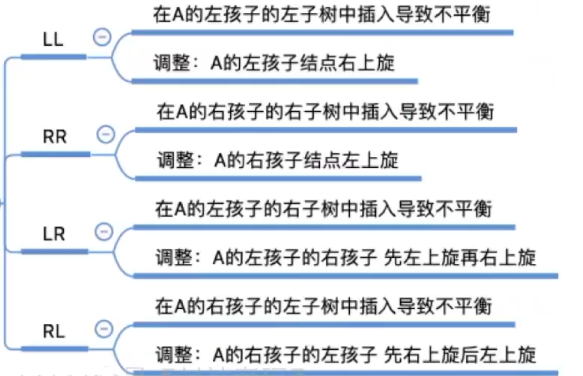
调制最小不平衡子树
LL在A的左孩子的左子树中插入导致不平衡
RR在A的右孩子的右子树中插入导致不平衡
LR在A的左孩子的右子树中插入导致不平衡
RL在A的右孩子的左子树中插入导致不平衡
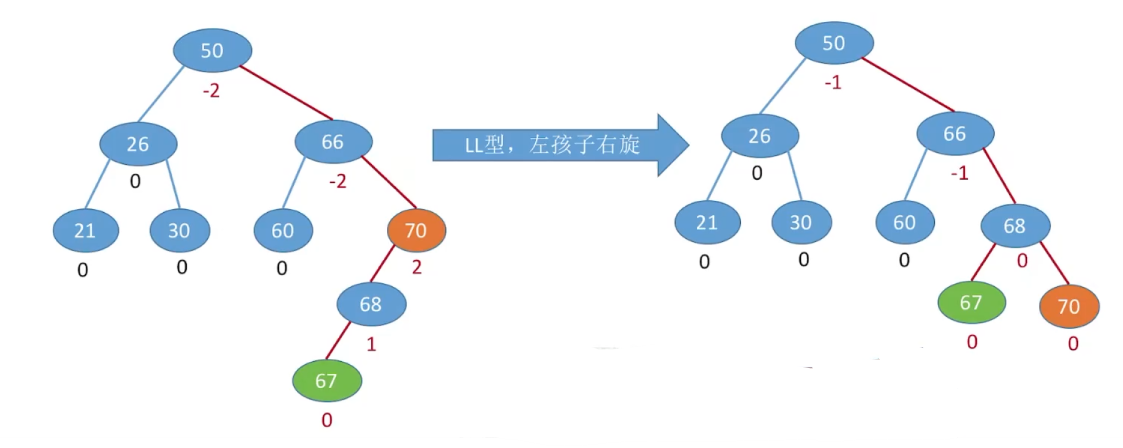
调整最小不平衡子树(LL)
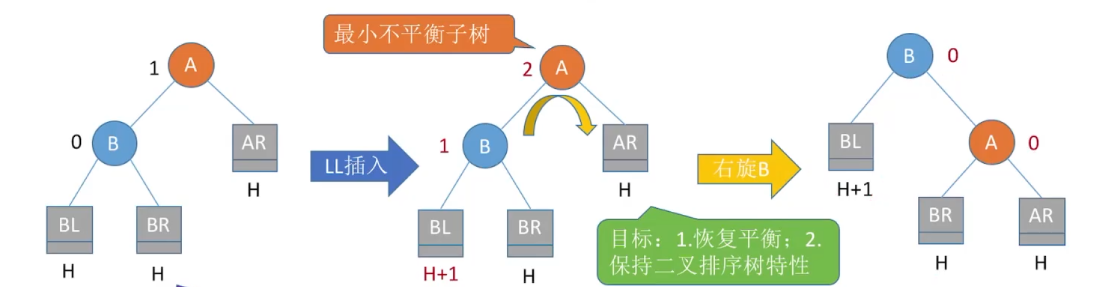
- LL平衡旋转(右单旋转)。由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。
调整最小不平衡子树(RR)
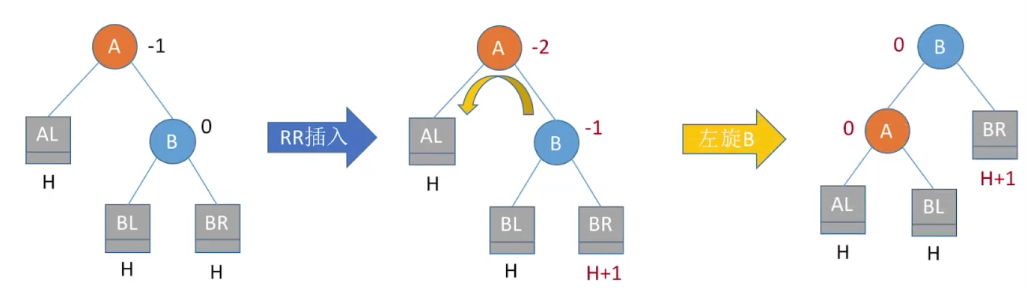
2)RR平衡旋转(左单旋转)。由于在结点A的右孩子®的右子树®上插入了新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点,将A结点向左下旋转成为B的左子树的根结点,而B的原左子树则作为A结点的右子树
代码思路
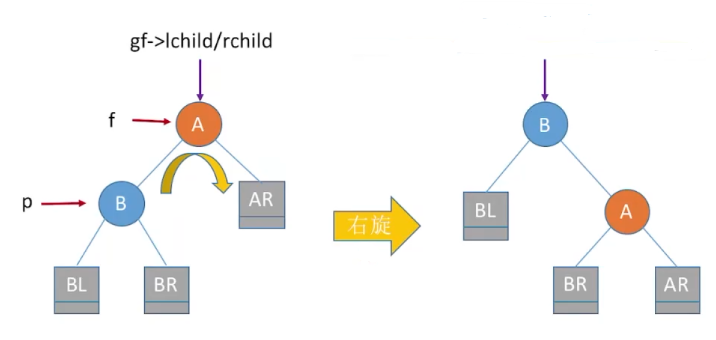
实现f向右下旋转,p向右上旋转:
其中f是爹,p为左孩子,gf为f他爹
1:f->lchild=p->rchild;
2:p->rchild=f;
3:gf->lchild/rchild=p;
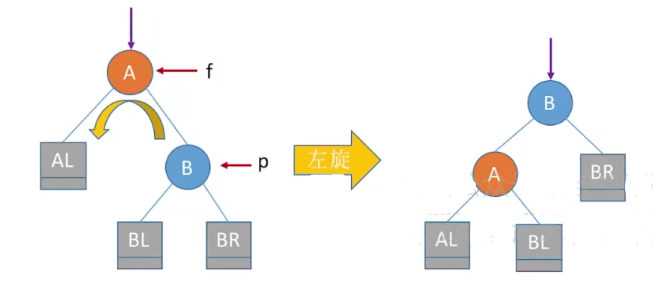
实现f向左下旋转,p向左上旋转:
其中f是爹,p为右孩子,gf为f他爹
1:f->rchild=p->lchild;
2:p->lchild=f;
3:gf->lchild/rchild=p;
调整最小不平衡子树(LR)
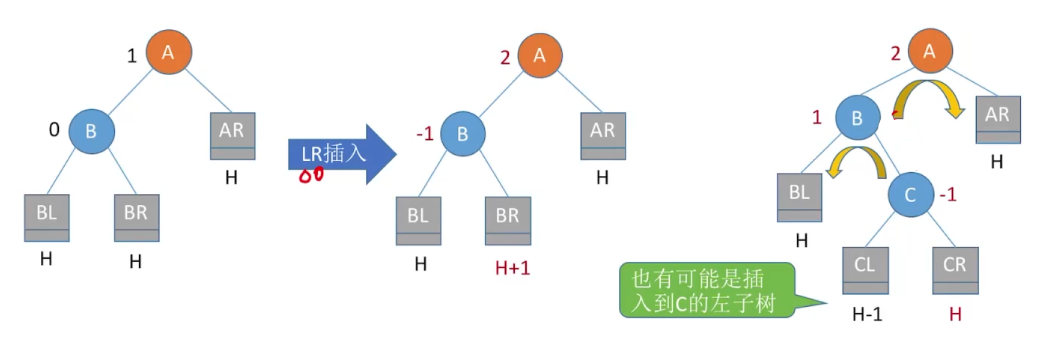
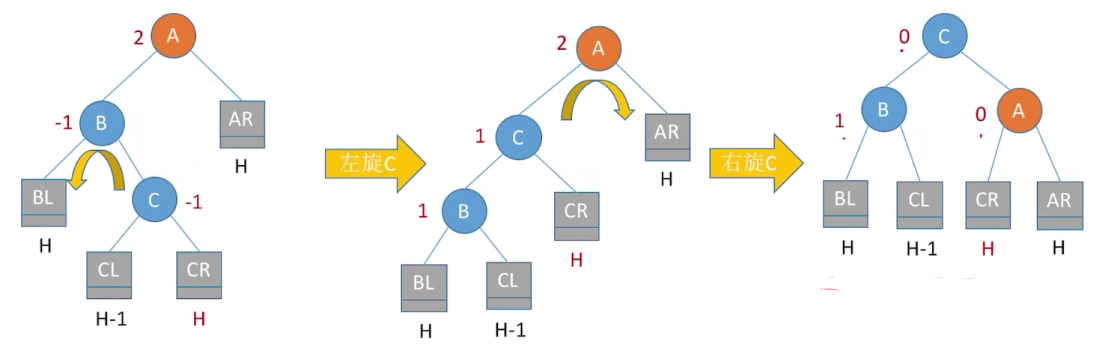
3)LR平衡旋转(先左后右双旋转)。由于在A的左孩子(L)的右子树®上插入新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先左旋转后右旋转。先将A结点的左孩子B的右子树的根结点c向左上旋转提升到B结点的位置,然后再把该c结点向右上旋转提升到A结点的位置
调整最小不平衡子树(RL)
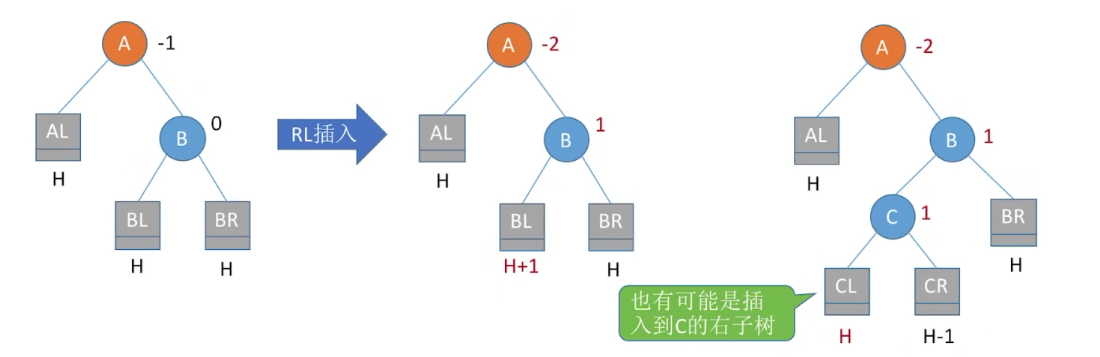
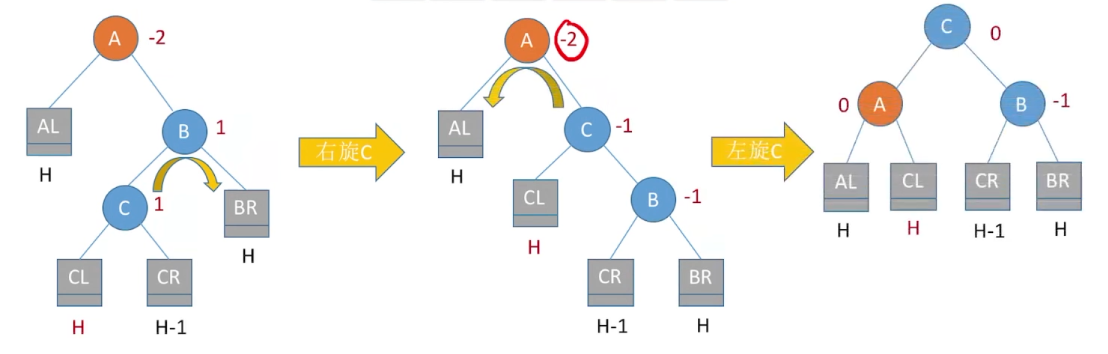
4)RL平衡旋转(先右后左双旋转)。由于在A的右孩子(R)的左子树(L)上插入新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置,然后再把该C结点向左上旋转提升到A结点的位置
查找效率分析
若树高为h,则最坏情况下,查找一个关键字最多需要对比h次,即查找操作的时间复杂度不可能超过O(h)

红黑树
为什么发明红黑树?
平衡二叉树AVL:插入\删除 很容易破坏“平衡”特性,需要频繁调整树的形态。如:插入操作导致不平衡,则需要先计算平衡因子,找到最小不平衡子数(时间开销大),再进行LL\RR\LR\RL调整
红黑树:插入\删除 很多时候不会破坏“红黑”特性,无需频繁调整树的形态。即使需要调整,一般都可以在常数级时间内完成
平衡二叉树:适用于以查为主、很少插入\删除的场景
红黑树:适用于频繁插入、删除的场景,实用性更强
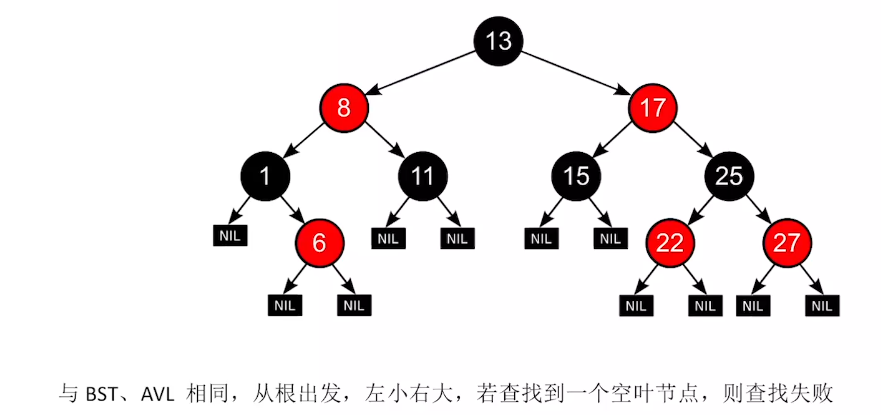
红黑树的定义
红黑树是二叉排序树->左子树结点值<=根结点值<=右子树结点值
与普通BST相比:
1、每个结点或是红色,或是黑色的
2、根节点是黑色的
3、叶结点(外部结点、NULL结点、失败结点)均是黑色的
4、不存在两个相邻的红结点(即红结点的父节点和孩子结点均是黑色)
5、对每个结点,从该节点到任一叶结点的简单路径上,所含黑结点的数目相同
struct RBnode{ //红黑树的结点定义
int key; //关键字的值
RBnode* parent; //父节点指针
RBnode* lChild; //左孩子指针
RBnode* rChild; //右孩子指针
int color; //结点颜色,如:0/1 表示 黑/红
}
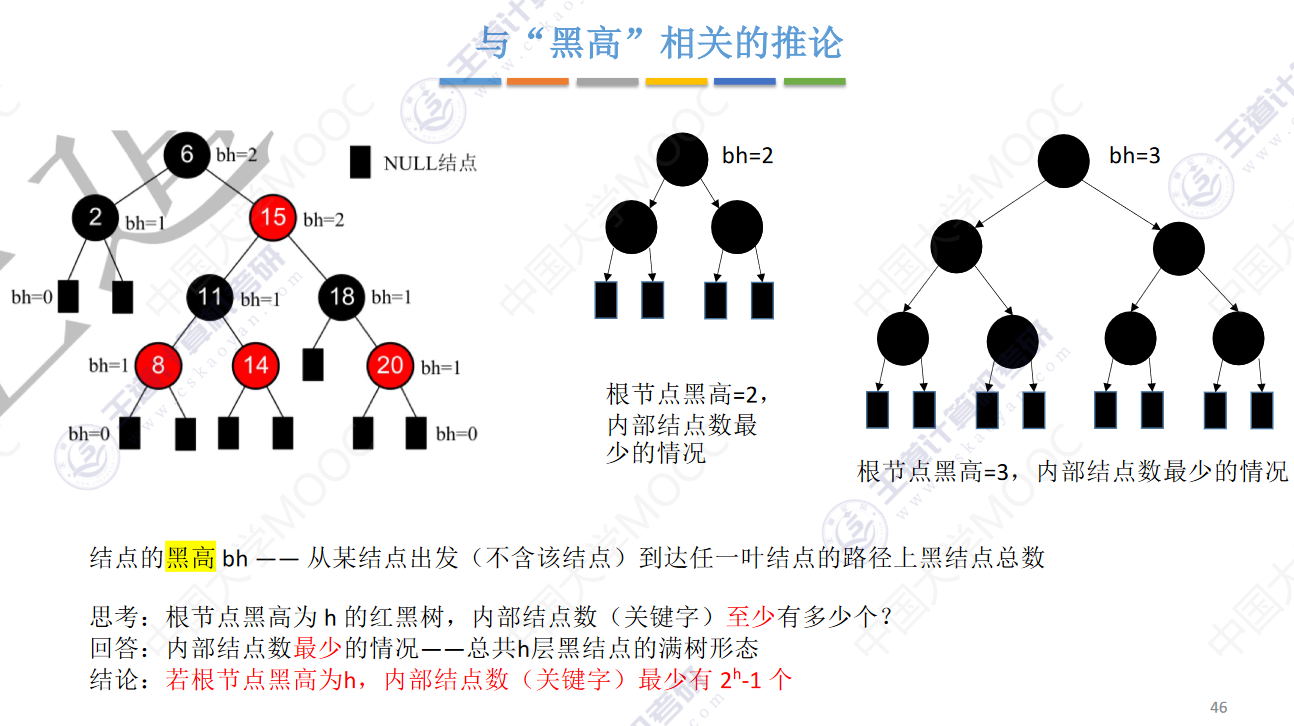
结点的“黑高”
从某结点出发(不含该结点)达到任一空叶结点的路径上黑结点总数

红黑树性质
1、从根节点到叶结点的最长路径不大于最短路径的2倍
2、有n个内部节点的红黑树高度h<=2log(n+1)
红黑树的查找
红黑树的插入
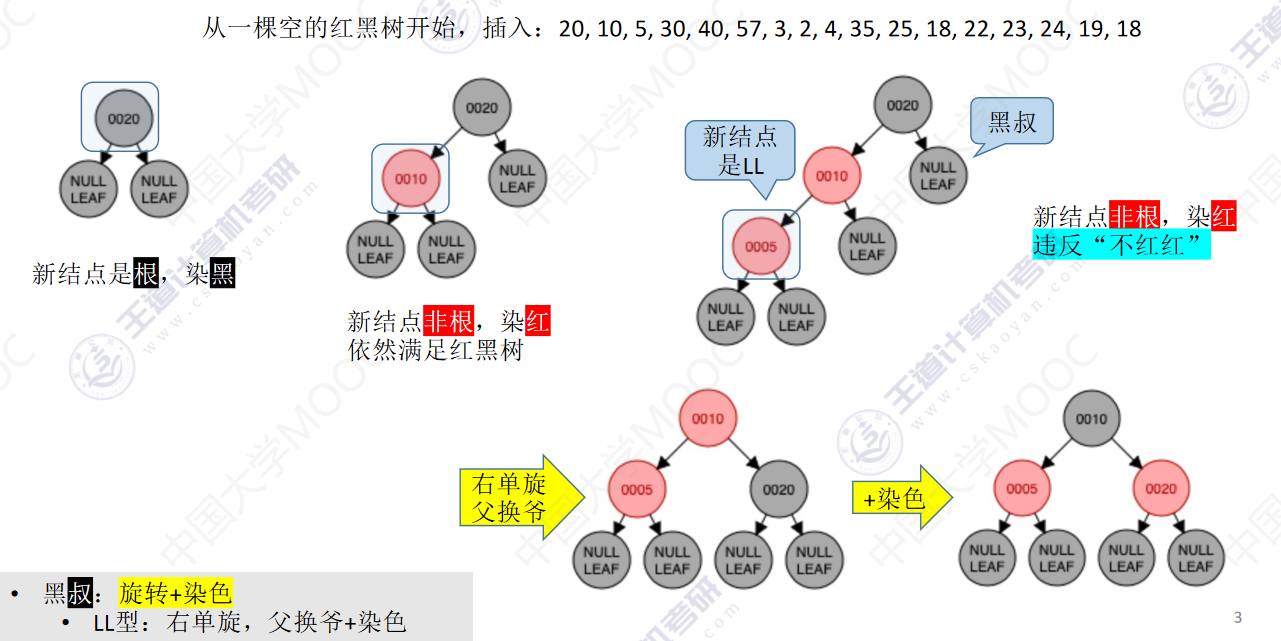
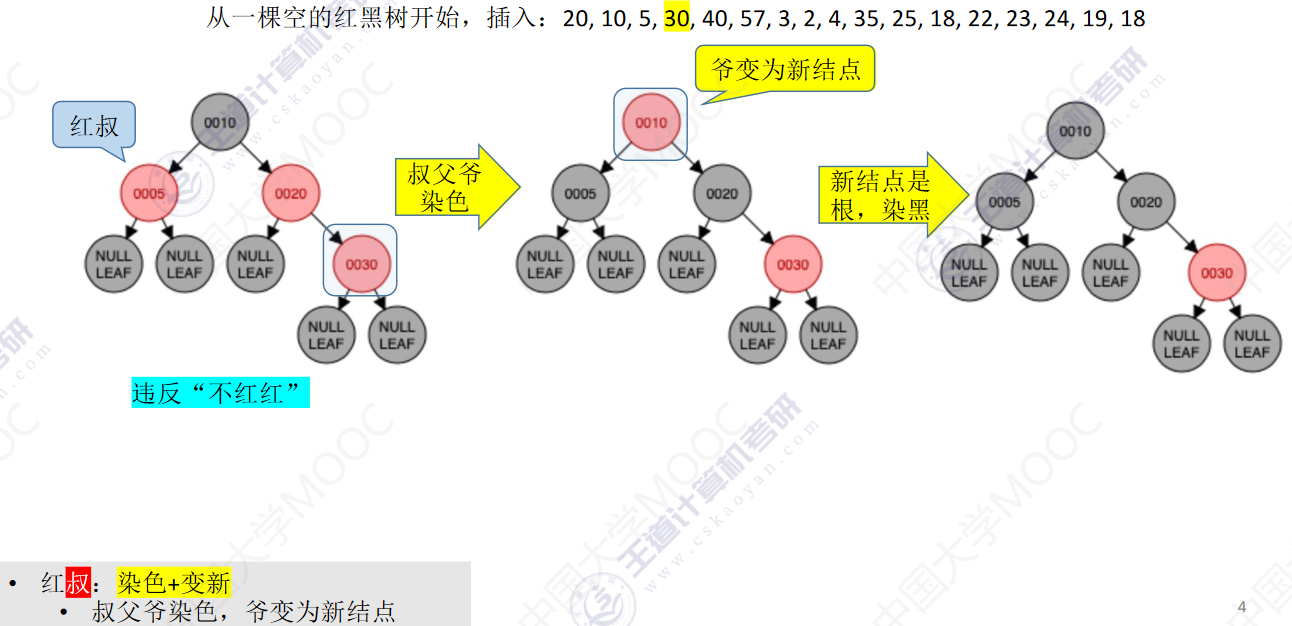
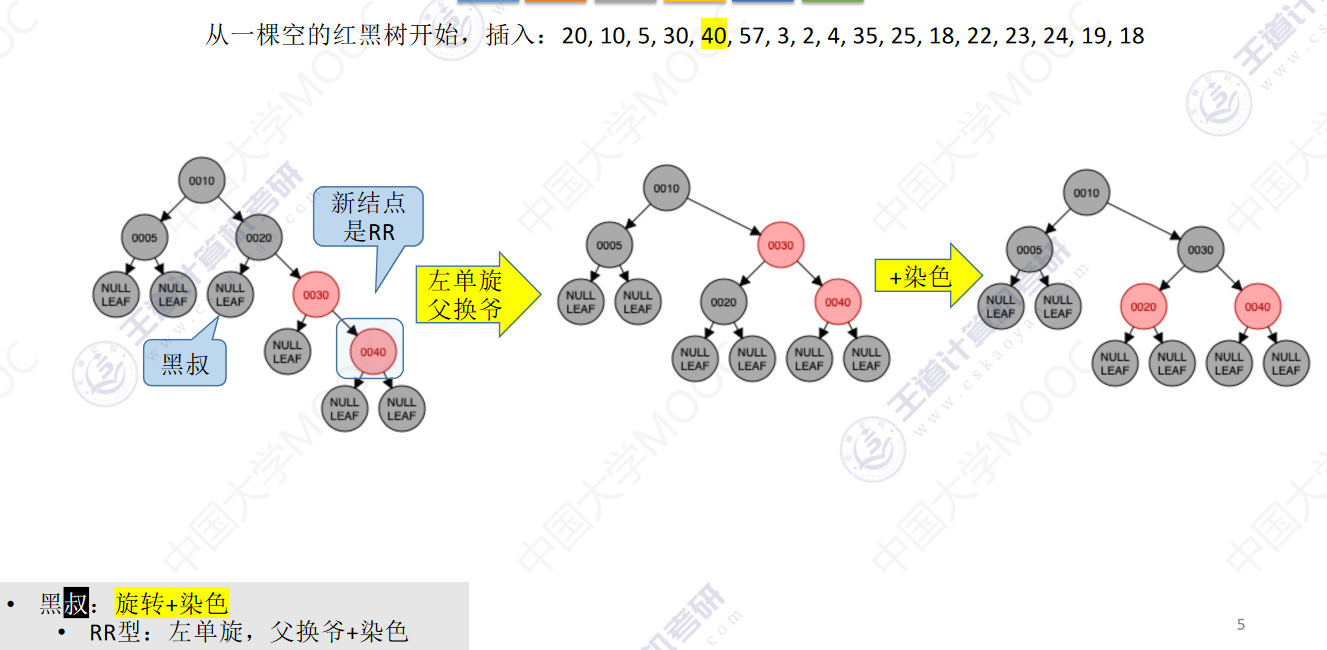
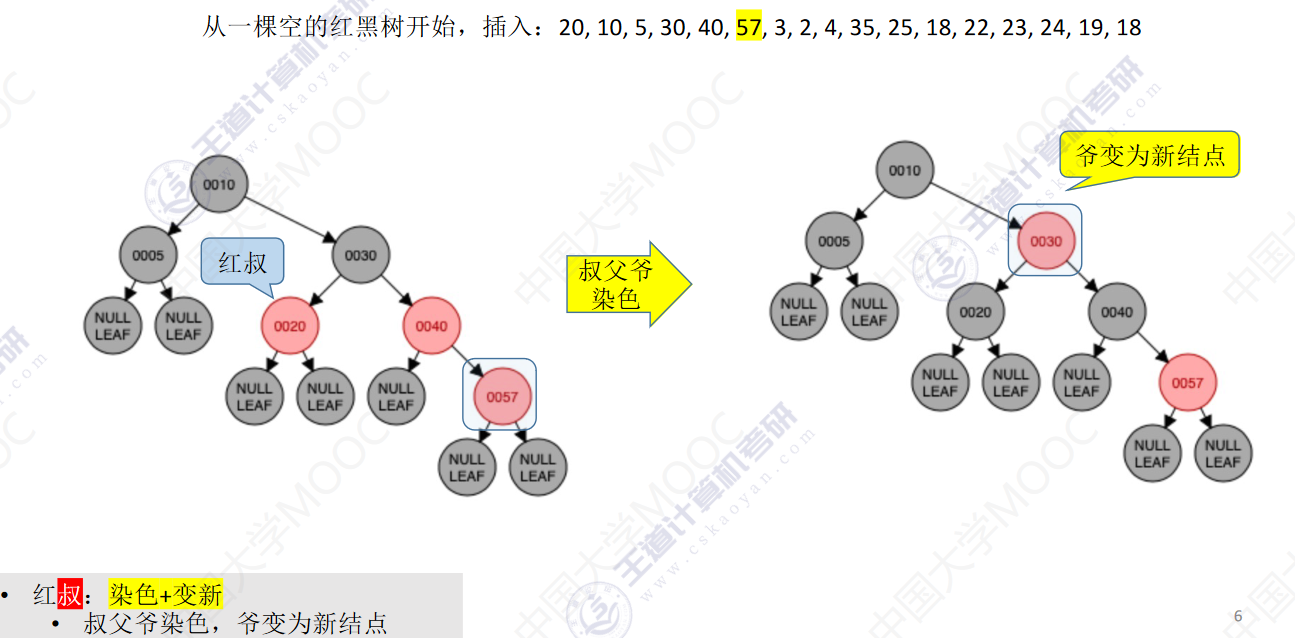
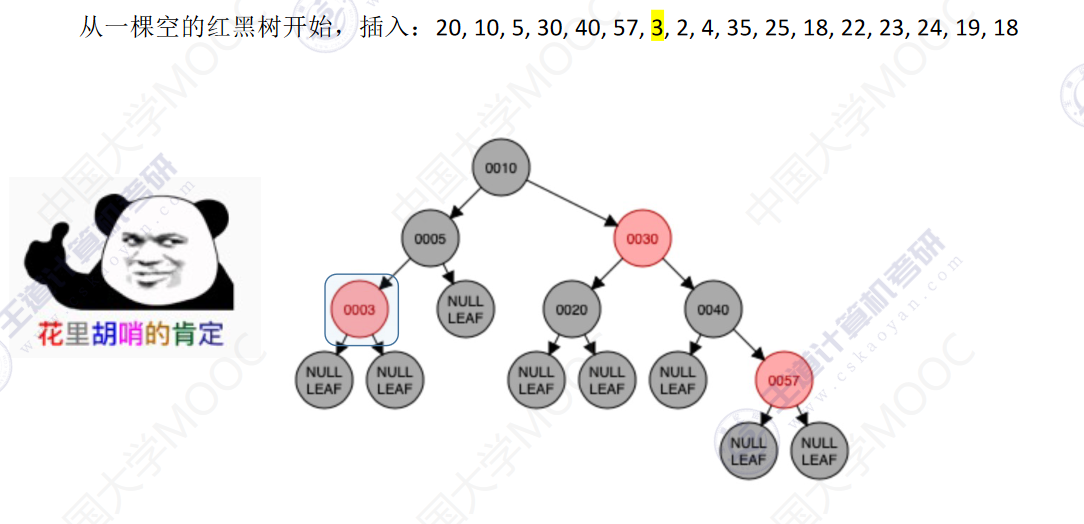
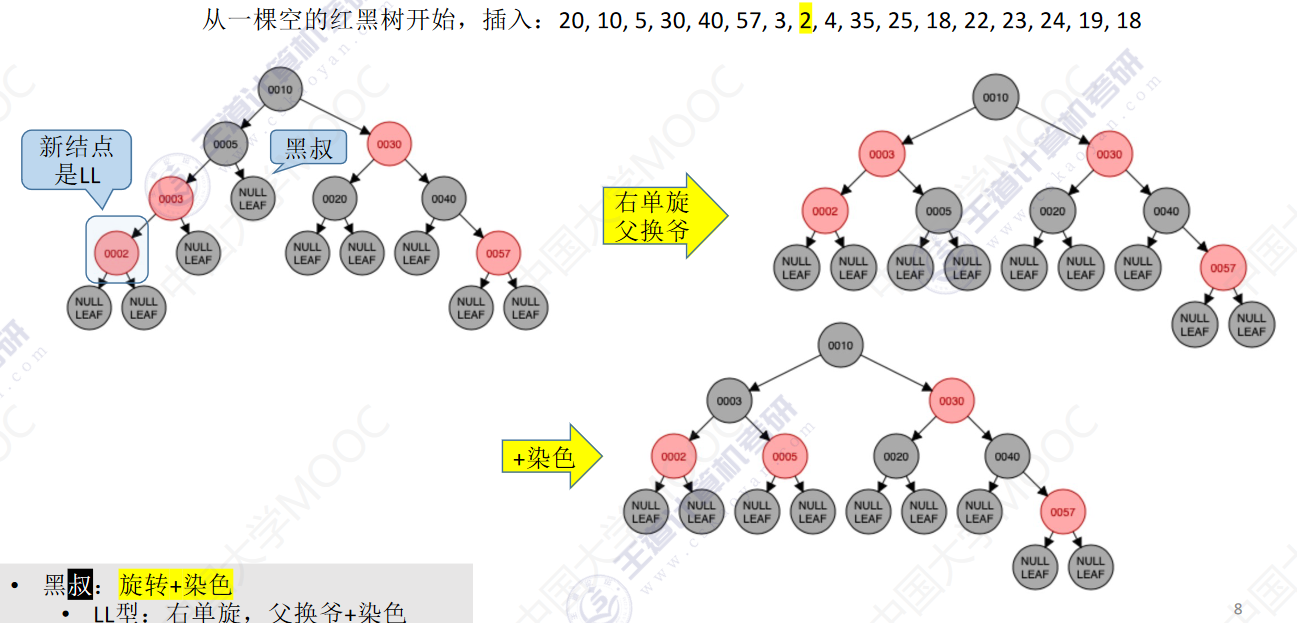
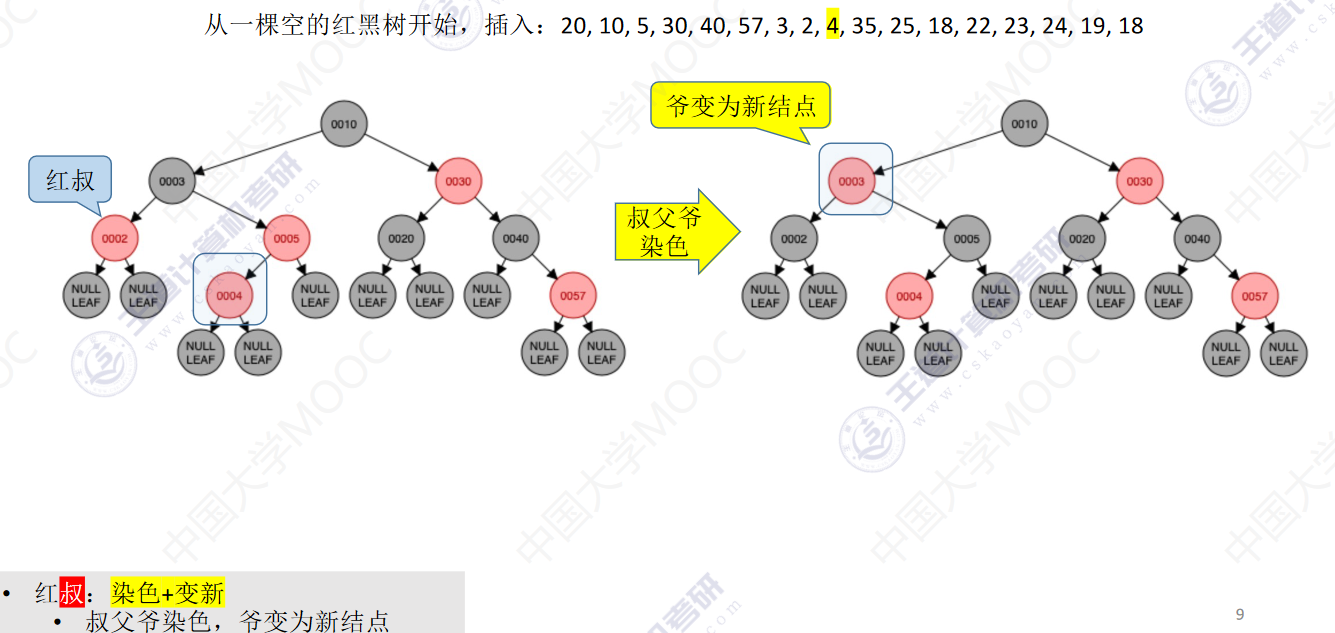
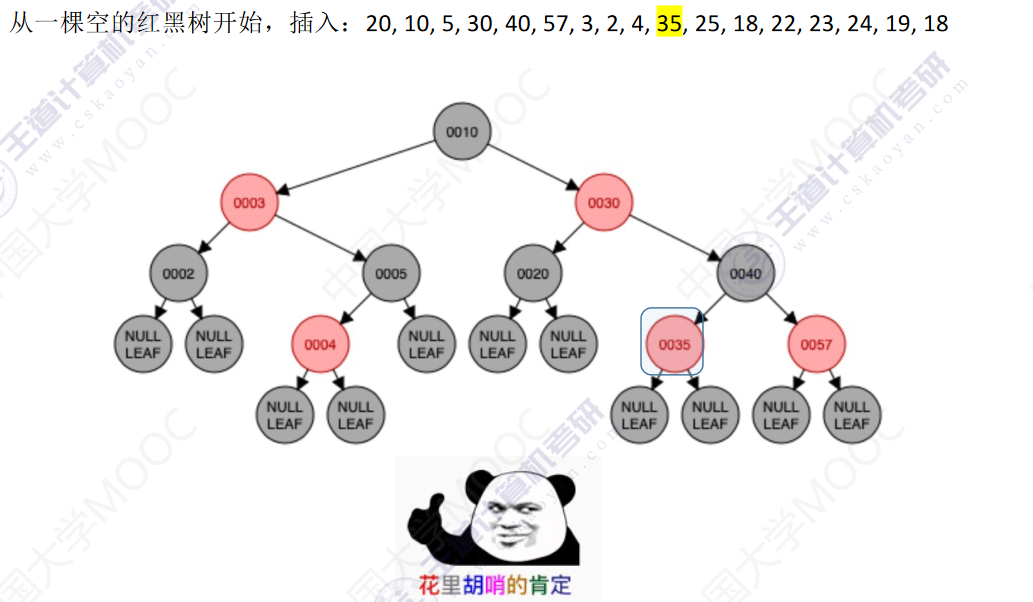
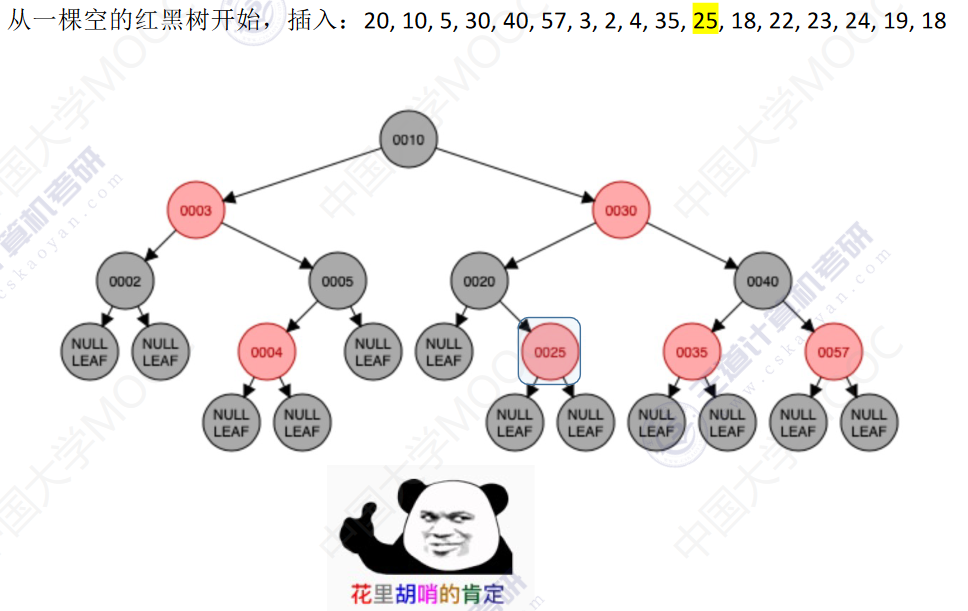
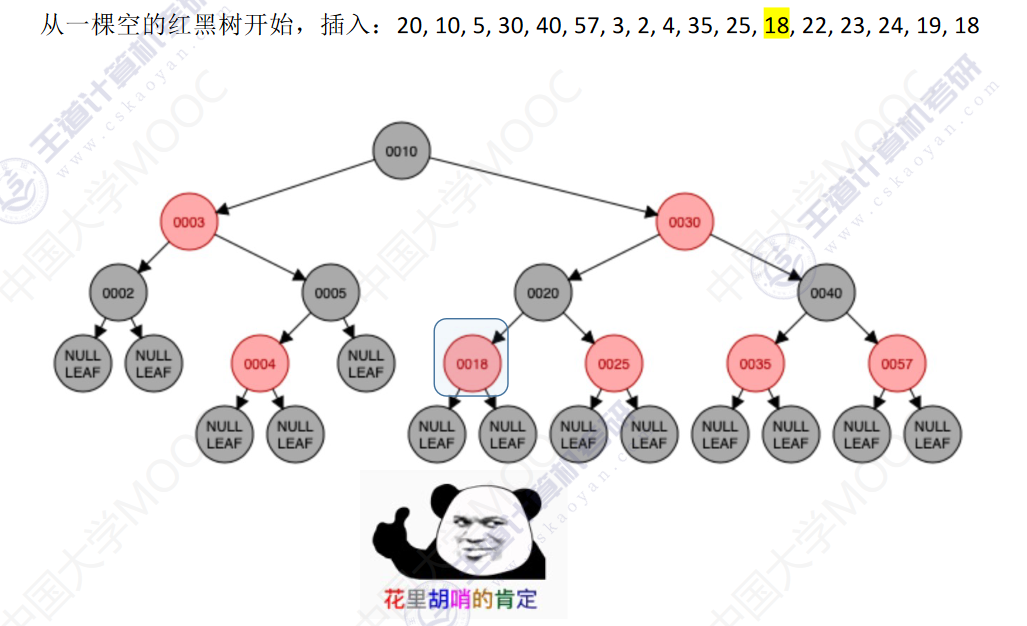
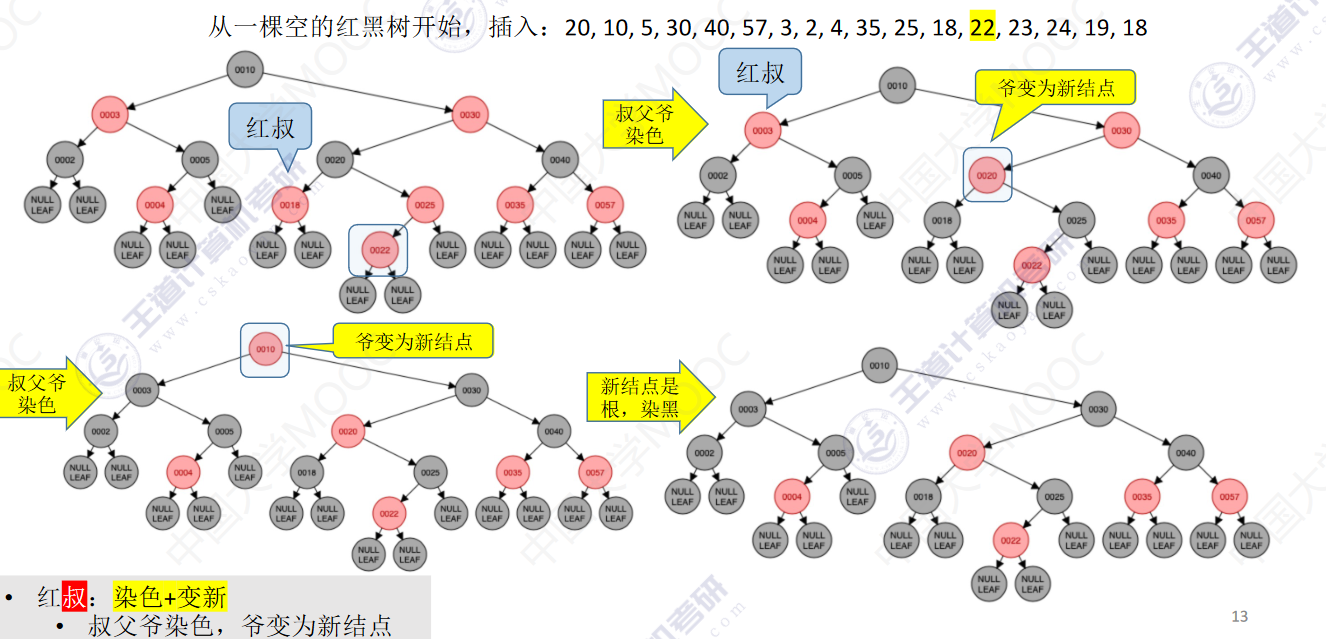
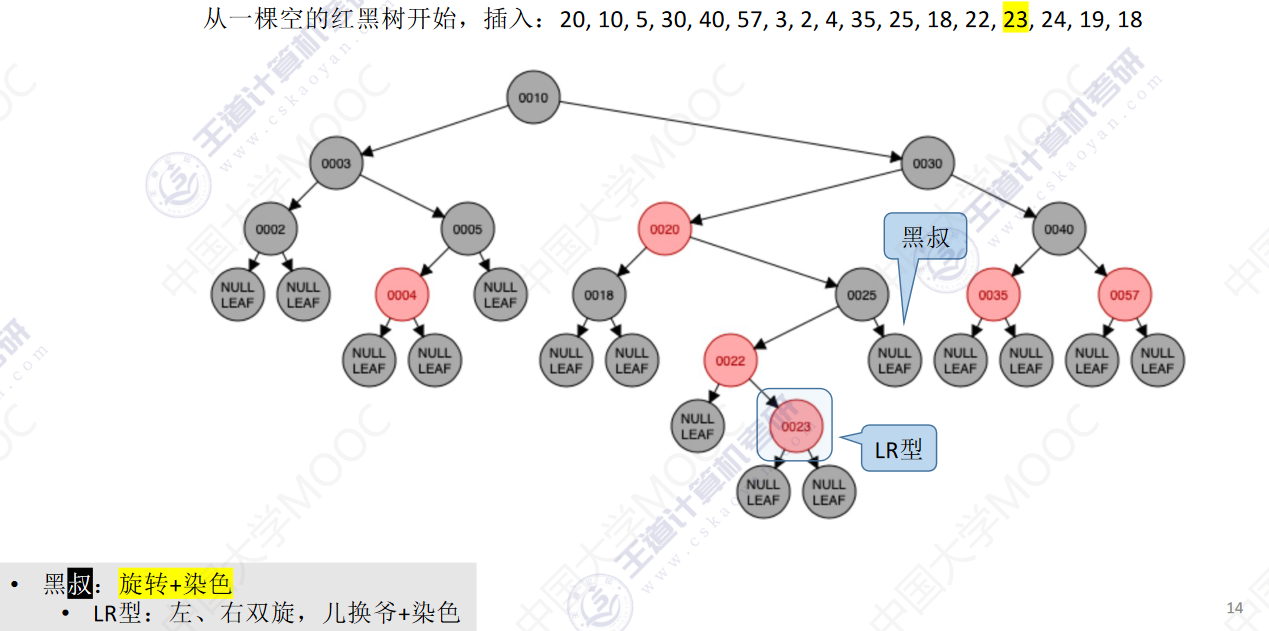
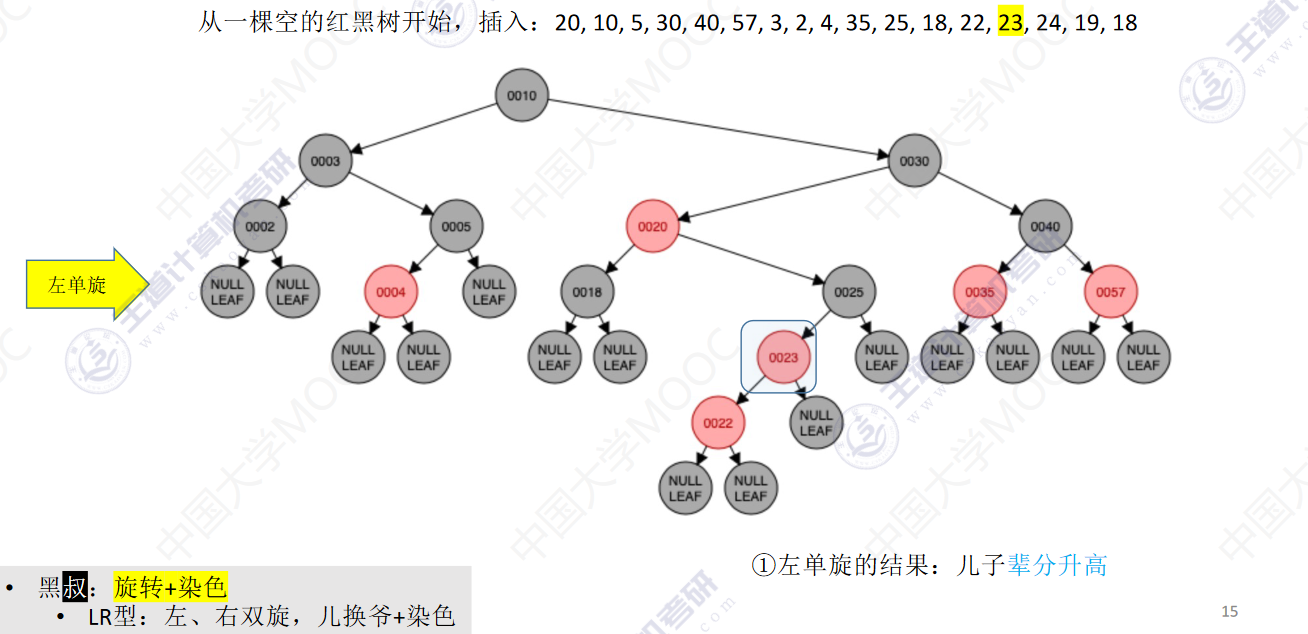
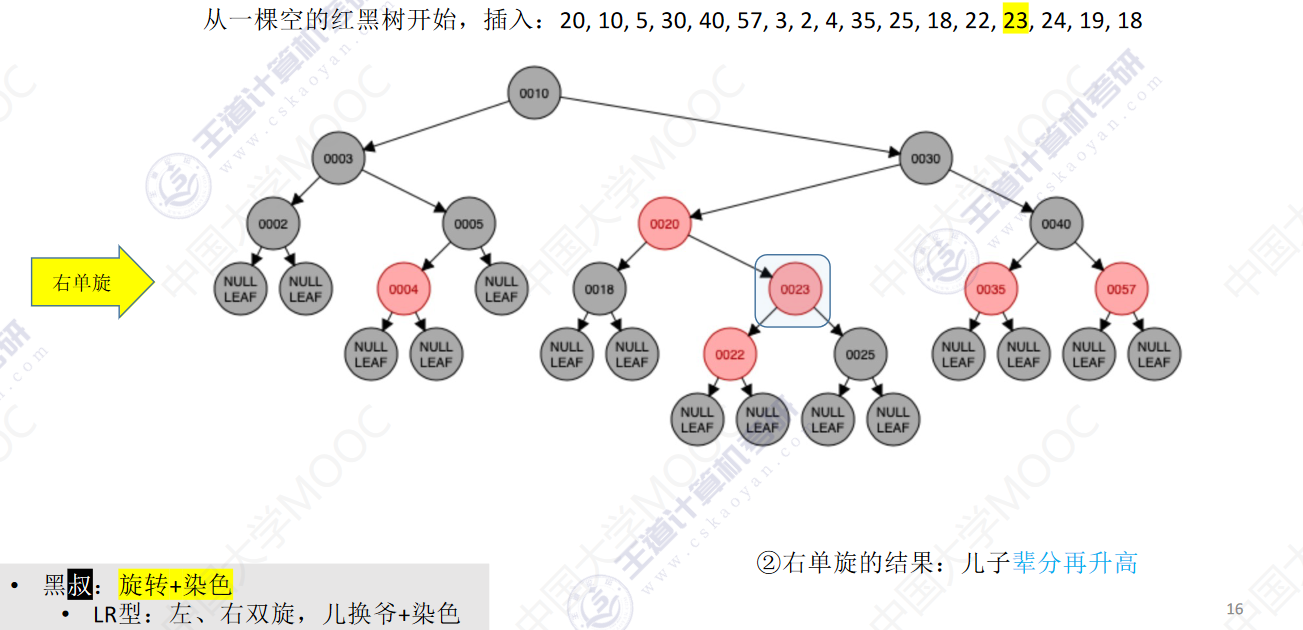
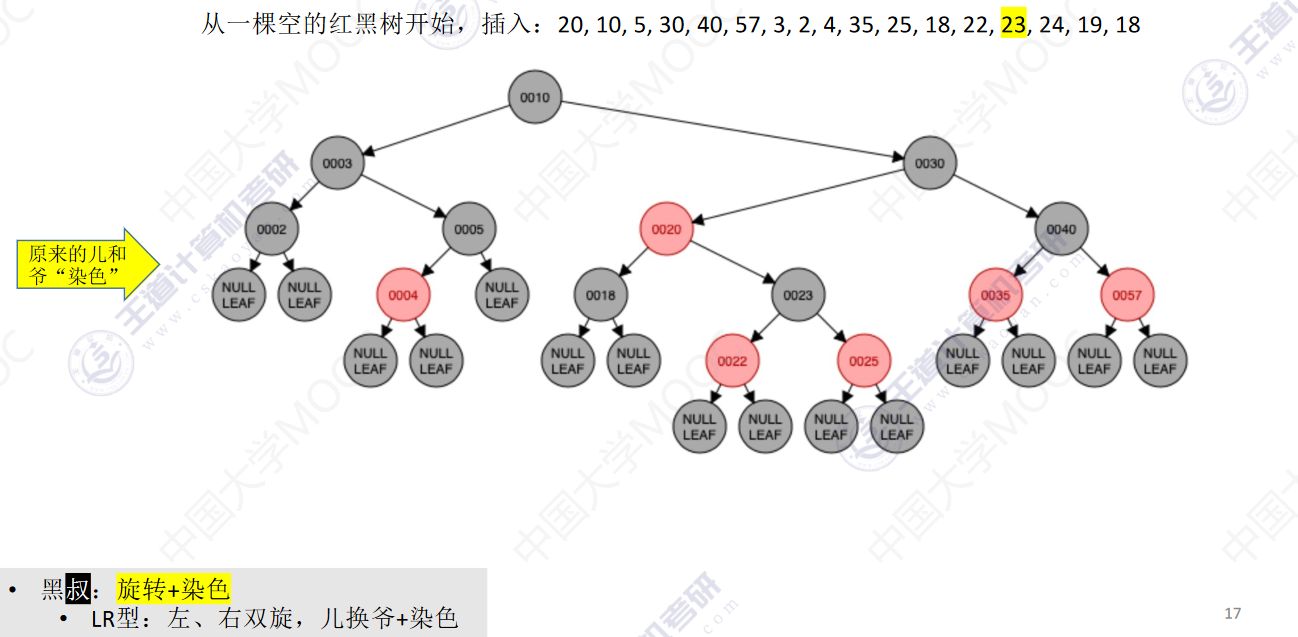
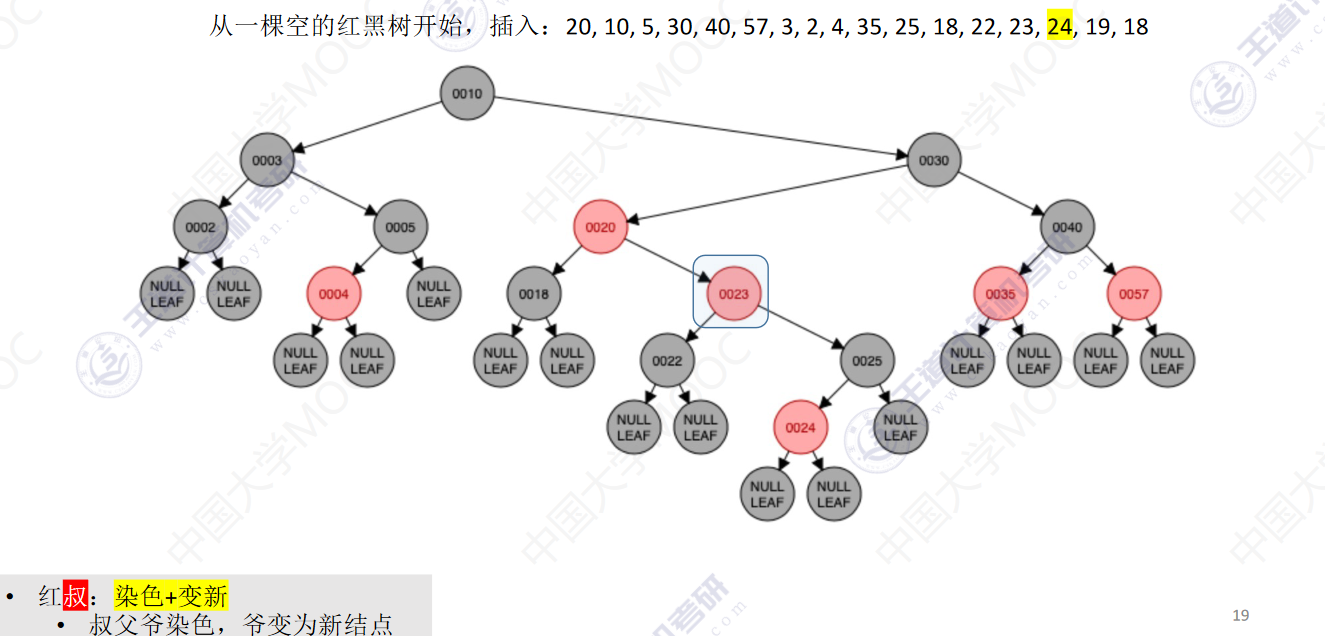
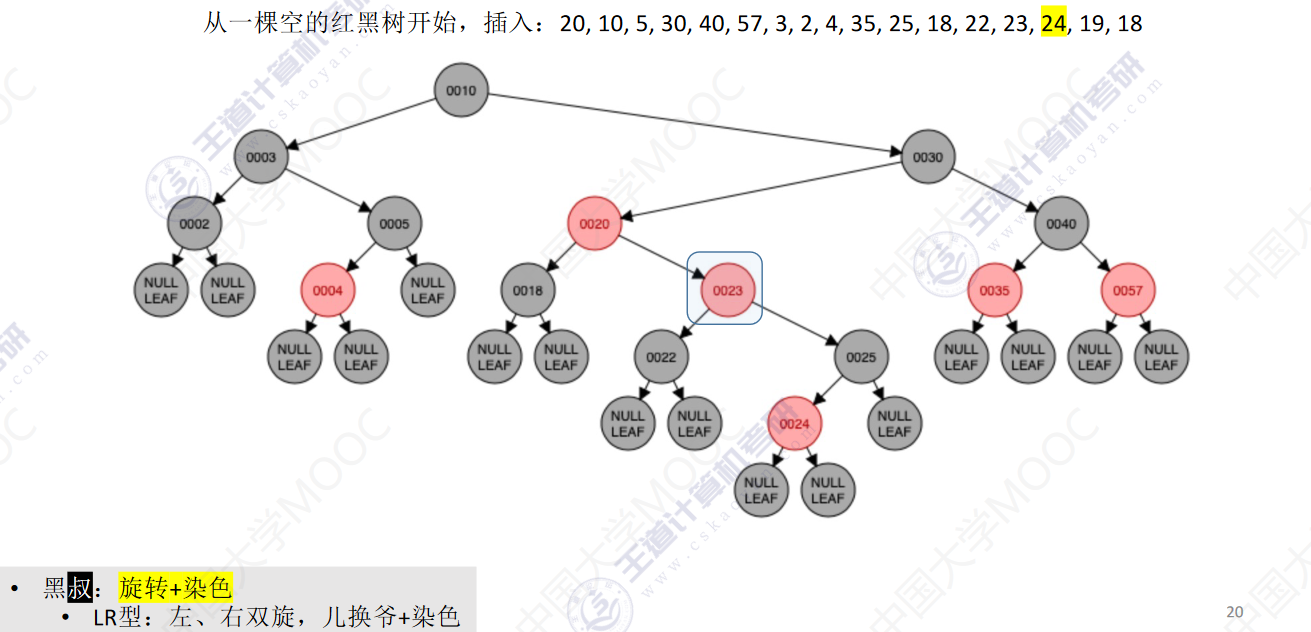
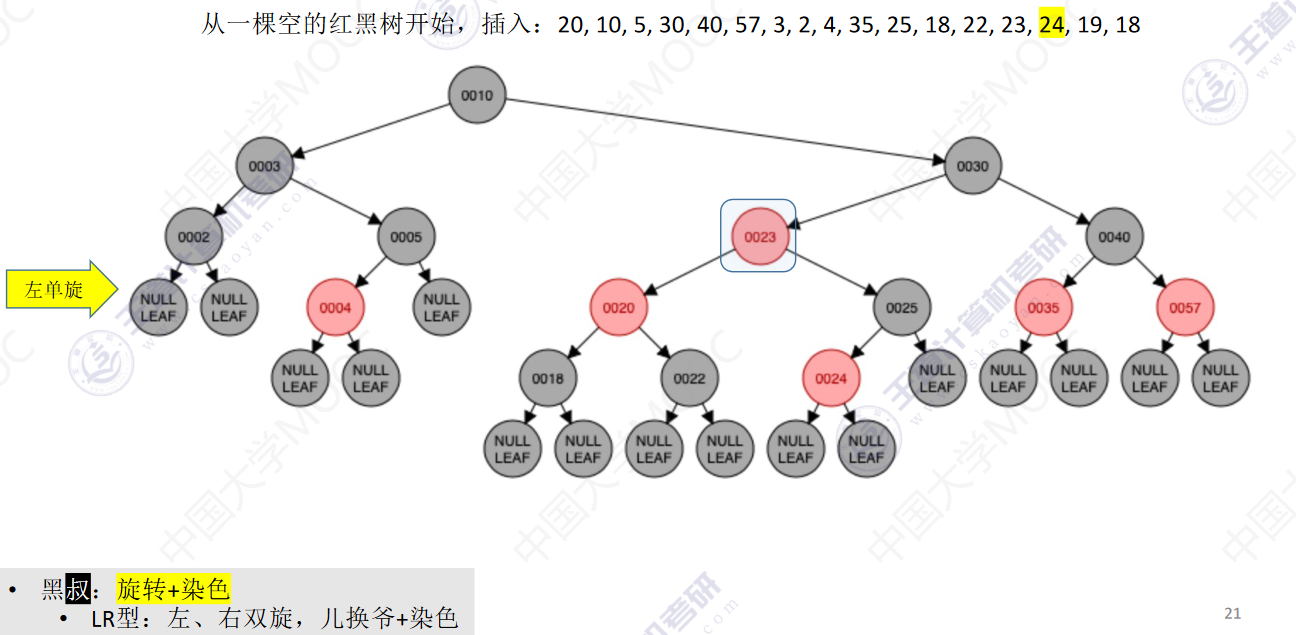
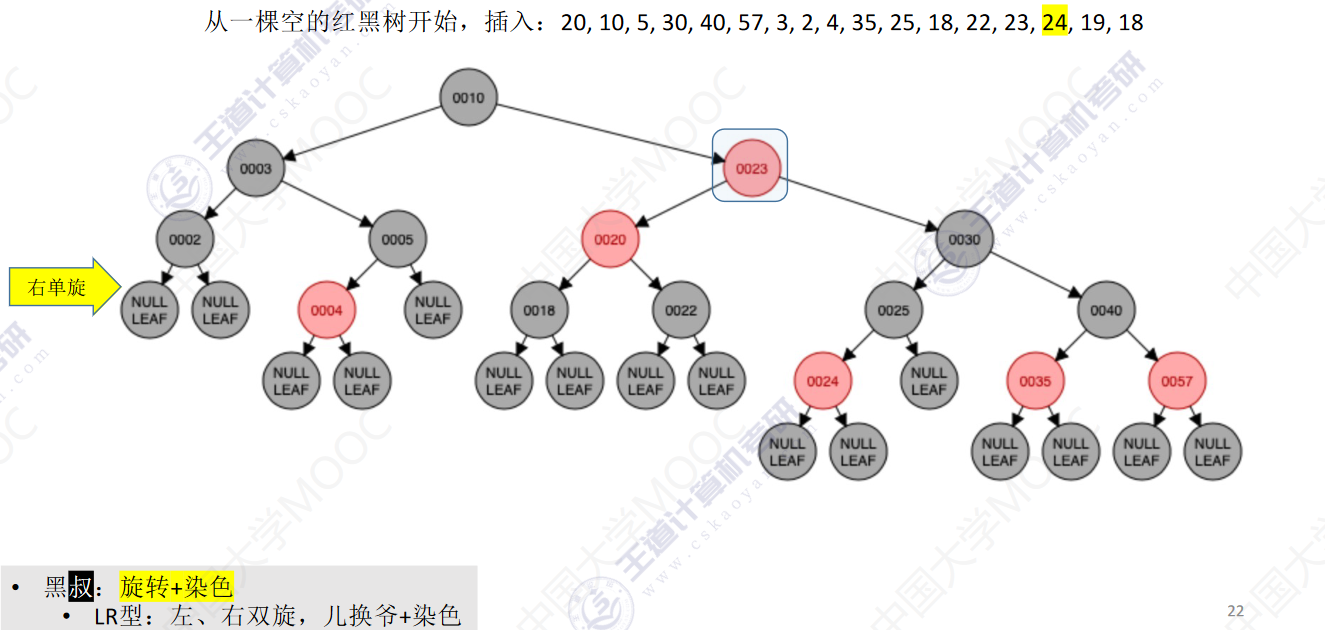
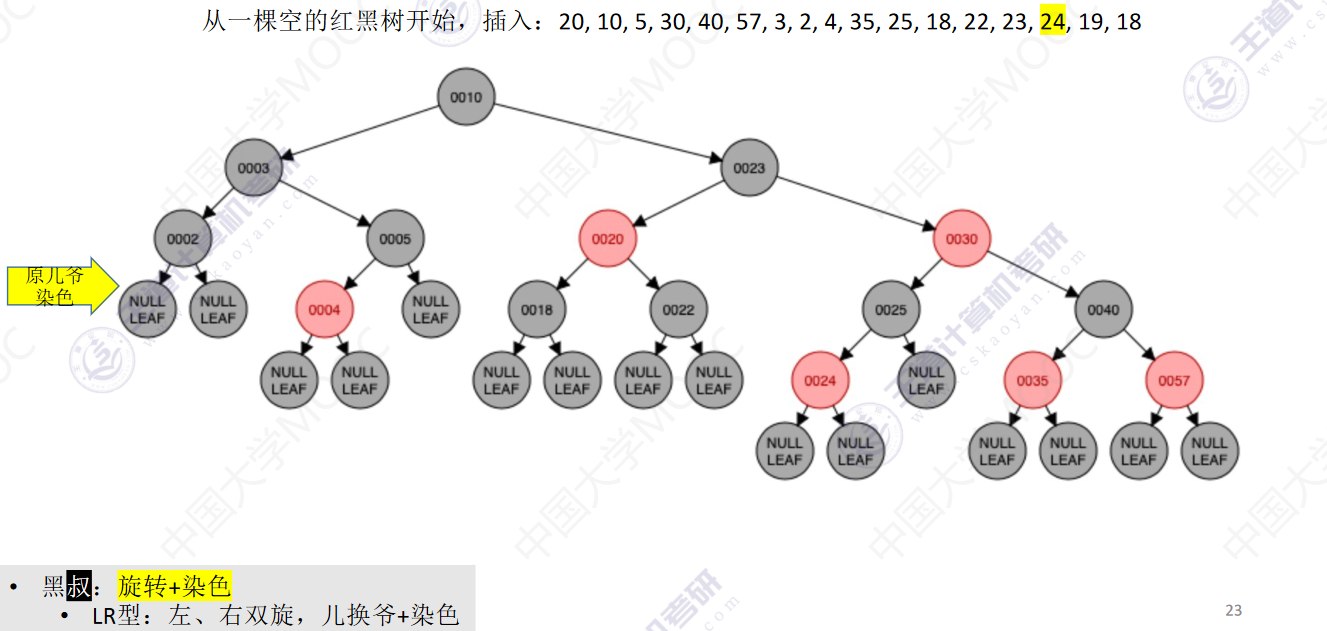
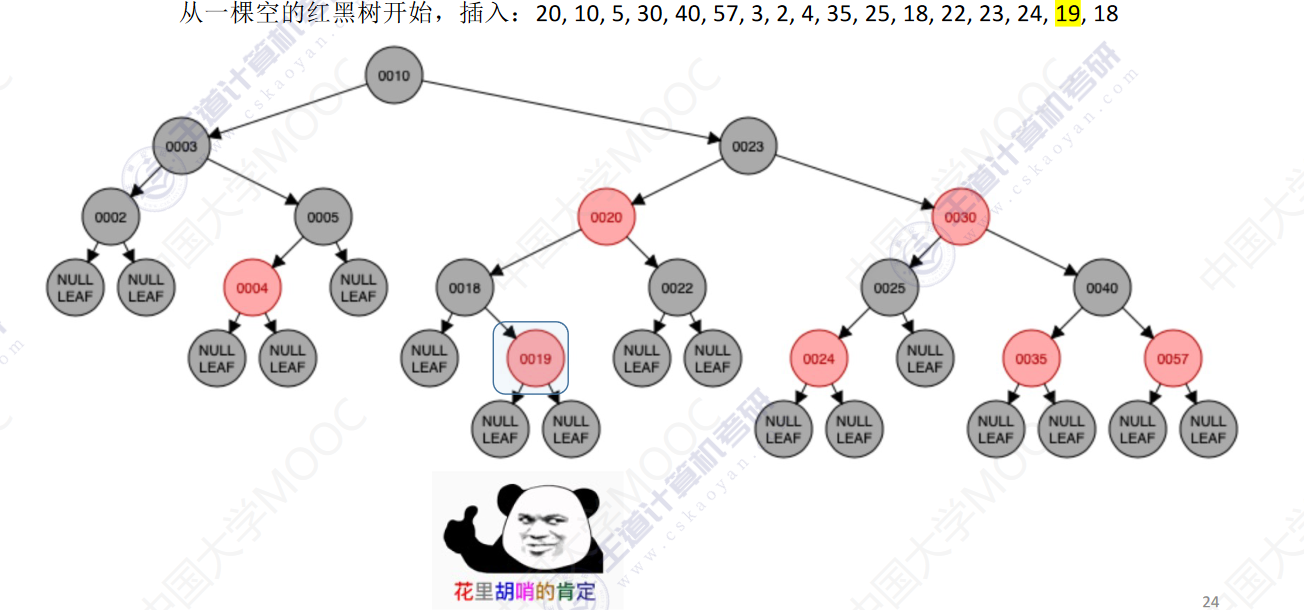
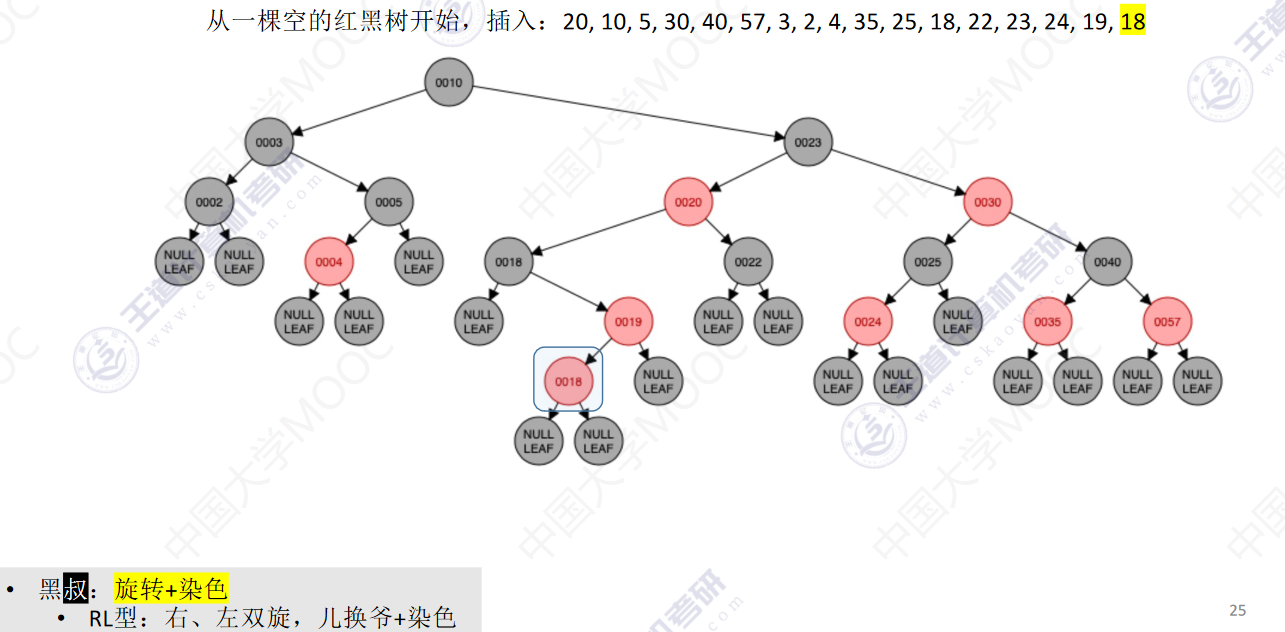
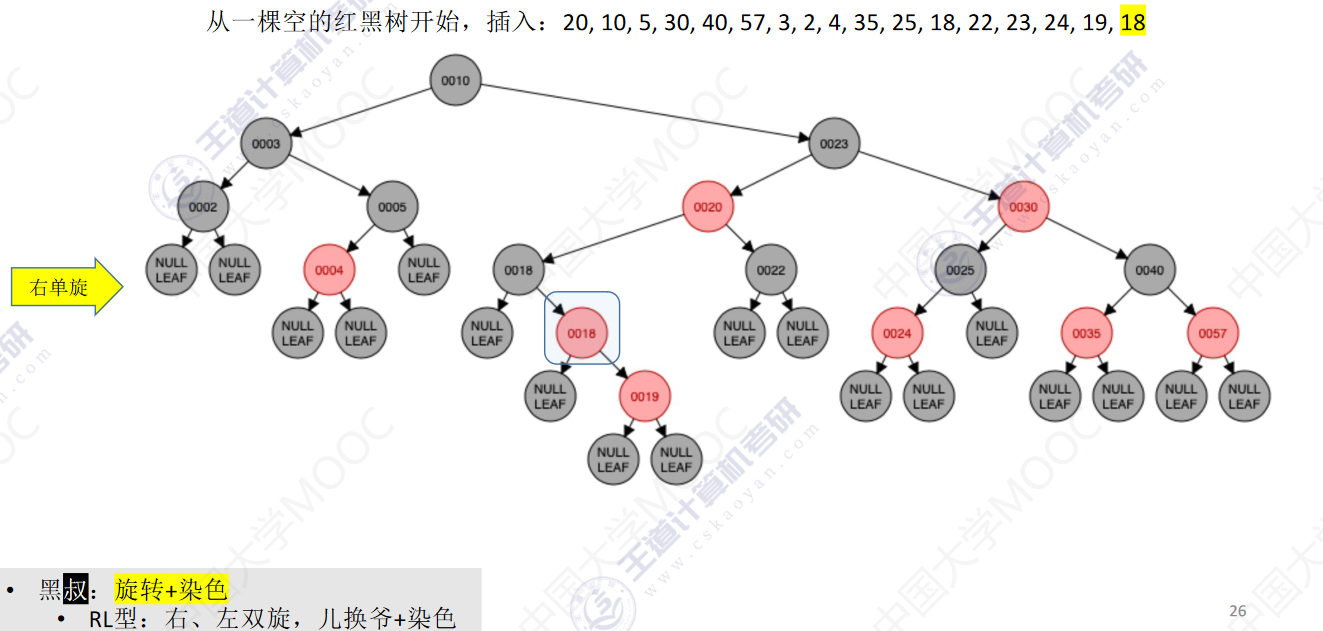
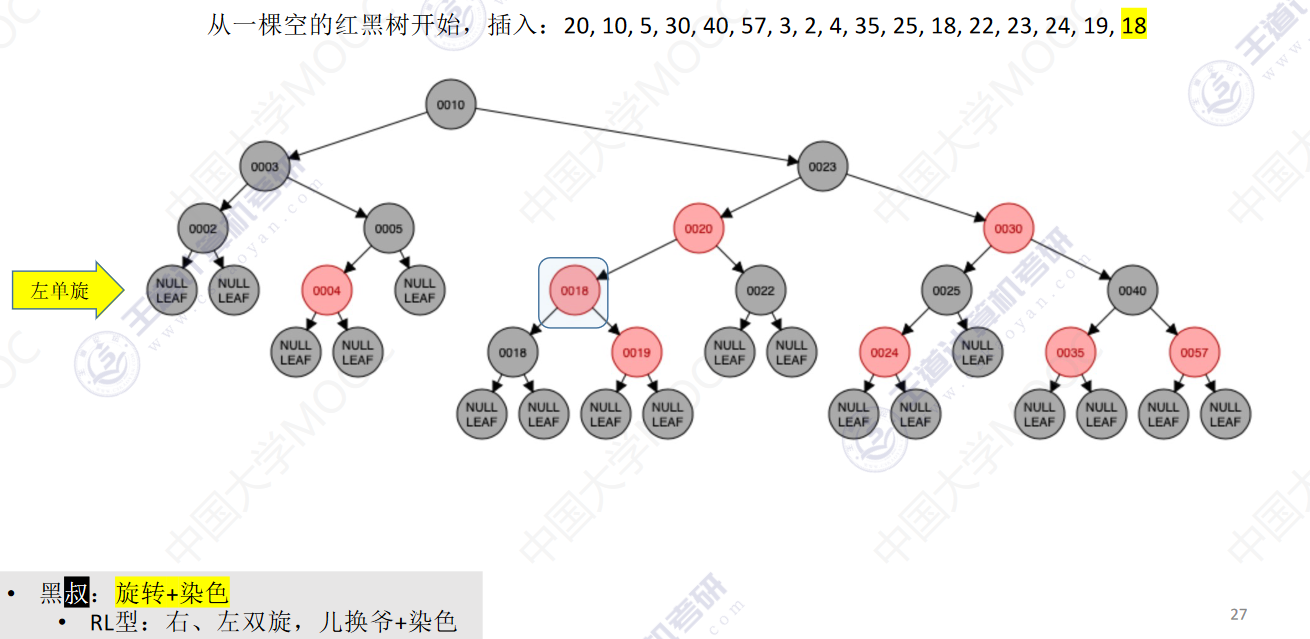
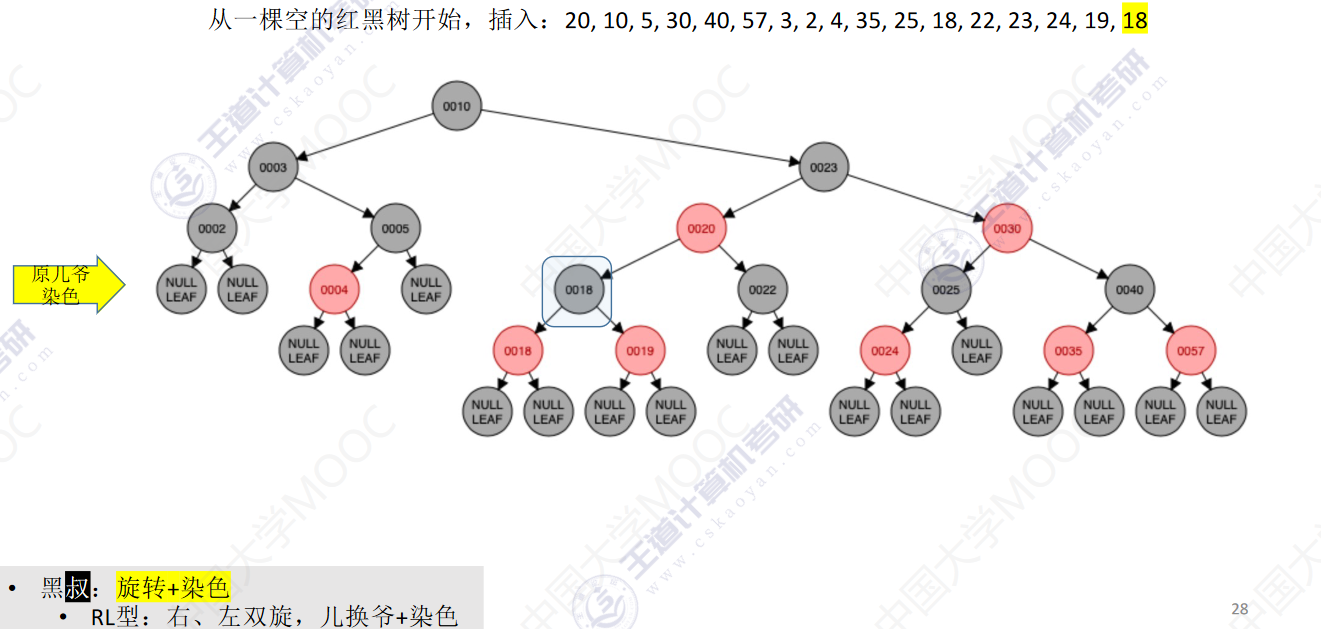
从一颗空的红黑树开始,插入:20,10,5,30,40,57,3,2,4,35,25,18,22,23,24,19,18
先查找,确定插入位置(原理同二叉排序树),插入新结点
新结点是根–染为黑色
新结点非根–染为红色
- 若插入新结点后依然满足红黑树定义,则插入结束
- 若插入新结点后不满足红黑树定义,需要调整,使其重新满足红黑树定义(看新结点叔叔的颜色)
- 黑叔:旋转+染色
- LL型:右单旋,父换爷+染色
- RR型:左单旋,父换爷+染色
- LR型:左、右双旋,儿换爷+染色
- RL型:右、左双旋,儿换爷+染色
- 红叔:染色+变新
- 叔父爷染色,爷变为新结点
- 黑叔:旋转+染色