一、说明
这是卡尔曼滤波器系列的第一部分。但这并不是另一本定义繁重的读物,它会给你带来一堆行话和方程式!在本文中,我们首先关注需要解决方案的问题(当然是卡尔曼滤波器),然后直观地了解卡尔曼滤波器。只有这样我们才会引入方程和数值例子来使我们的想法具体化。
可是等等!如果没有实现,每个工具都是不完整的 - 在接下来的文章中,我们还将用 Python 构建卡尔曼滤波器。
因此,本系列分为以下几个:
- 直观了解卡尔曼滤波器、Alpha-Beta滤波器;
- 形式贝叶斯滤波器和卡尔曼滤波器;
- Python 中的一维卡尔曼滤波器从头开始;
- Python 中的二维卡尔曼滤波器从头开始。
在本文中,我们对卡尔曼滤波器有一个直观的理解,并正式介绍构成下一部分卡尔曼滤波器基础的 Alpha-Beta 滤波器。
让我们从两个现实世界的问题陈述开始,而不是从卡尔曼滤波器的无聊术语定义开始。使用它们,我们建立了对卡尔曼滤波器的直觉。
二、问题陈述
2.1 示例 1 — 机器人定位
想象一下,巴黎卢浮宫博物馆决定购买一台移动自主机器人,以在夜间巡逻整个博物馆内部。该机器人具有差动运动模型,并配备摄像头。此外,机器人还可以通过使用摄像头图像的先进物体识别系统来识别周围的物体。
为了完成巡逻任务,机器人需要不断估计自己在环境中的位置,并计算到达目的地的路径,同时避开障碍物。当前的问题是——机器人将如何估计其当前位置?
解决这个问题的一种可能的方法是每秒积累机器人的运动数据。从初始点 (0,0) 开始,通过将机器人里程计的线性和角运动值相加,可以使用基本数学随时估计机器人的位置。
然而,事情要复杂得多。研究小组注意到,机器人行进的距离越远,它对自身位置的信念(估计)就越错误。经过仔细检查,发现机器人执行的运动与里程计传感器读取的值略有不同。随着时间的推移,这种差异的积累只会让机器人更加相信自己的位置。以下是里程传感器读取的线性运动值(以米为单位)以及机器人在六次情况下执行的实际线性运动。

因此,我们无法估计该机器人的位置如何随时间变化,因为传感器信息充满噪音。我们做什么?在提出解决方案之前,我们先看另一个例子。
2.2 示例 2 — 计算机视觉
想象一下,您正在尝试跟踪视频流中的足球。然而,由于相机噪声、运动模糊和检测噪声等因素,帧中检测到的球位置存在噪声。因此,我们无法准确估计球的位置如何随时间变化。让我们更进一步讨论这个问题。
在实际场景中,某些帧会存在遮挡。那么,如果我们需要维持每一帧的球位置估计,即使某些帧中存在遮挡,会发生什么?
现在,让我们让它变得更加困难。如果框架中有 2 个球并且我们想要跟踪它们的移动情况该怎么办?每个球都会有一个ID,我们当然不能更换ID。好吧,如果我们很天真,我们只会继续获得每帧的2 个球位置(检测 1和检测 2 )的检测结果。我们可以在每对帧中选择最近的球并分配相同的 ID。但如果其中一项检测缺失 20 帧怎么办?我们没有估计机制来预测 20 帧后球的位置。到那时,在真实情况下,也许球会交叉,我们将无法再比较连续两帧中的位置。如果测量缺失,我们没有可以估计位置的系统。
为了跟踪球随时间的运动,需要一种可以结合多个帧的信息来更准确地估计球的位置的方法。
三、卡尔曼滤波器——一种直觉
一般来说,在这两个问题陈述中,我们的目标是估计对象的状态- 示例 1 中的机器人位置和示例 2 中的球位置。
卡尔曼滤波器是一种工具,可以帮助您高精度地估计状态,即使您正在使用的测量结果有噪声或不确定。它通过使用数学模型根据前一个时间实例t-1中的位置及其移动方式(状态估计)来预测时间实例t的状态值应为多少。然后,它将该预测与在时间t接收到的传感器测量值进行比较,并根据差异调整其估计(状态更新)。
让这个稍微正式一点,卡尔曼滤波器有两个步骤:
- 状态预测:根据时间 t-1 的估计值来预测时间 t 的状态值。它使用状态传播/外推模型来预测该值。我们稍后会讨论这个状态外推模型是什么样的。
- 状态更新:将状态预测的预测与测量值(均针对时间t)进行比较,并根据差异更新/调整其对时间 t 的最终估计。此步骤使用传感器/探测器。
为什么这两个步骤都很重要-
—如果我们没有状态预测步骤,我们将只能受到容易产生噪声的传感器/探测器值的支配。因此我们的估计也容易出现噪声和漂移。
—如果我们没有状态更新步骤,我们只会有一个状态外推模型,它告诉我们在理想世界中状态应该如何随时间变化。但世界并不理想。将理想值变为真实值的步骤将会缺失
四、让我们用关于状态预测和状态更新的新知识再次看看我们的两个问题陈述
3.1 示例 1 — 机器人定位
在示例 1 中,通过向系统添加状态外推模型(此处称为运动模型),机器人的导航算法可以考虑机器人的预期运动,并使用它来纠正里程计读数中的任何错误。
运动模型通常基于机器人运动的物理原理,例如其速度和加速度,并用于预测机器人随时间的运动。例如,使用等速运动模型是很常见的。使用简单的运动定律,根据机器人在时间t-1的位置和速度,它可以预测机器人在时间 t 的位置。此外,该模型假设两次实例之间的速度恒定,而不是永远恒定。如果机器人的速度或方向发生变化,状态更新步骤将纠正下一个状态预测步骤的速度值。
然后将预测的运动与里程计传感器测量的实际运动进行比较,并使用任何差异来更新运动模型。通过不断更新运动模型,机器人的估计位置随着时间的推移变得更加准确。
注意 - 传感器融合是进一步改善定位结果的另一种机制。但这超出了本系列的范围。
3.2 示例 2 — 计算机视觉
在示例2中,除了每个时间步的状态更新中的检测值之外,添加状态外推模型(状态预测步骤)可以帮助使用运动模型来估计球的位置。
本质上,我们使用状态预测和状态更新步骤来结合我们关于状态应如何数学演化的知识和测量值。嗯,卡尔曼滤波器喜欢来自不同来源的数据。没有数据点是没有用的!
五、重新审视这个概念
卡尔曼滤波器的工作原理是根据当前状态预测下一个时间实例t的状态。它使用数学模型来做到这一点。 然后,在下一个时间点t,卡尔曼滤波器将其预测与传感器输出进行比较。预测与实际位置之间的差异用于调整球位置的估计,使其更加准确。
把它想象成和朋友玩猜谜游戏。你的朋友向你扔了一个球,但你看不清楚,因为有其他玩家挡住了。在你的朋友扔球之前,你尝试根据球现在的位置和移动的速度来猜测它会去哪里。然后,当球靠近时,您可以更清楚地看到它,并在您错误的情况下调整您的猜测。当球移动时,你在每个实例中不断执行此操作,并且你可以更好地猜测它会去哪里。
天真地说,你的大脑就像卡尔曼滤波器一样工作。它试图预测下一次球的位置。但是,如果球以意想不到的方式弯曲,您的大脑会将这个数据点与其现有的预测模型合并,并更新模型。这就是卡尔曼滤波器的全部内容!
六、Alpha-Beta 滤波器:卡尔曼滤波器的基础
现在您已经对卡尔曼滤波器是什么以及它的用途有了一个粗略和基本的了解,让我们退后一步,分析一个详细显示每个步骤的实际示例。但在本文中,我们构建了一个更简单版本的卡尔曼滤波器,称为Alpha-Beta 滤波器。卡尔曼滤波器是一种带有更多假设的 Alpha-Beta 滤波器。但我们目前使用 Alpha-Beta 滤波器构建正式基础,并在下一部分中将其发展为卡尔曼滤波器。
让我们想象一下,蜂鸟队正在参加印地自主挑战赛,并且正在其中一场比赛之前进行一项实验。他们的自动驾驶赛车配备了新的后翼,团队希望测量汽车的改进。测试内容是他们的小车匀速直线前进,小车通过天线与团队通信,如下图所示

天线还用于测量汽车在每个时间戳tᵢ 的距离,其中0 ≤ i ≤ n。天线和赛车之间的距离(以米为单位)由与每个tᵢ相关联的xᵢ表示。我们可以假设,无论汽车有多远,该天线都能够测量距离。
为了测量距离,天线发送广播信号,汽车接收到该信号后将其发回。通过时间差可以推算出汽车的速度。Δ t表示天线两次测量之间的时间间隔。对于我们的动态运动模型,我们假设汽车以恒定速度移动(注意 - 不要担心!状态更新步骤将考虑实际速度变化)。因此,我们可以将这个例子的系统动态模型描述如下:
![]()
![]()
将这两个方程翻译成英语,我们可以说当前机器人的距离xₙ等于过去的距离xₙ₋₁(这里我们累加部分距离,假设机器人从距离 0 开始)加上时间间隔, Δ t乘以 先前的速度。此外,由于我们假设汽车以恒定速度移动,因此前一个时间戳的速度等于当前的速度。
这两个方程组成了所谓的状态外推方程。这个名字是因为这个方程组将当前状态(汽车和天线之间的距离)推断到下一个状态(预测)。这里需要强调的是,这个方程组因情况而异,因为它取决于系统动力学。一般状态外推方程有一个矩阵表示法,但我们将在本系列的下一篇文章中详细介绍它。
继续,我们假设这个天线能够每两秒测量一次汽车的距离,Δt = 2。此外,我们说初始距离为0,x₀ = 0 m,估计的汽车速度为55 m/s 。通过状态外推方程,我们可以预测汽车在时间 1 时的目标位置(距离):
![]()
时间 1 的目标速度预测:
![]()
然而,在时间 1,天线测量距离z1等于 95 m,而不是预期的 110 m。预测距离和测量距离之间存在 15 m 的差异。在这种情况下,蜂鸟团队提出了两个可能的原因:
- 天线测量不精确;
- 自动赛车在测量之间改变了速度。新的速度将为 (95 — 0)/2 = 47.5 m/s 。
您认为其中哪一个才是真正的原因?让我们来看看。
赛车位置的状态更新方程为:
![]()
其中 α 在每次迭代中计算 (αₙ = 1/n)。然而,我们假设 α 因子在本例中是恒定的。
总之,α的大小取决于天线测量精度。对于高精度读数,我们可以选择较高的 α,从而更加重视测量zₙ。如果 α = 1,则估计距离等于测量范围:
![]()
另一方面,如果 α = 0,则测量没有意义:
![]()
将此方程应用到我们的示例中,对于 α = 0 和 α = 1,我们将分别得到以下公式:
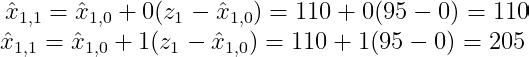
既然引入了α因子,我们继续分析,考虑另一种可能。速度的状态更新方程如下:
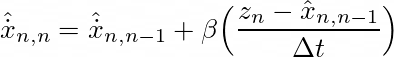
β的值与天线的精度水平有关。假设天线所有测量值中大约 69% (1σ) 的精度为 5 m,则预测距离和测量距离之间的 15 m 差距很可能是由于汽车速度的变化造成的,因为该差距高于精度。因此,蜂鸟团队应该将β设置为一个较高的值,例如β=0.9。在这种情况下,估计速度为:
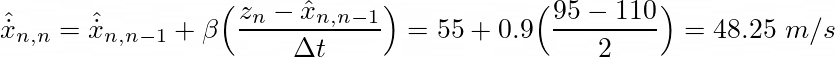
另一方面,假设所有天线测量中 69%(1σ) 的精度为 25 m。那么,15 m 的差异可能是由于天线测量误差造成的。在这种情况下,我们应该为 β 因子定义一个较低的值,因为测量结果不可靠。对于 β = 0.2,我们有:
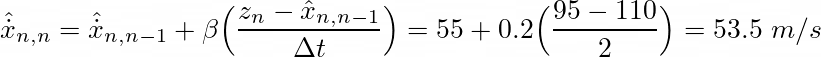
如果赛车的速度从 55 m/s 变为 47.5 m/s,我们会在六个测量周期后看到这一点(运行上述方程六次,β = 0.1)。如果差异是由测量误差引起的,则连续测量将位于预测位置的前面或后面。因此,平均而言,目标速度不会改变。
通过此分析,我们提出了构成天线状态更新方程的方程组。该方程组又称为α—β航迹更新方程(或α—β航迹滤波方程)。
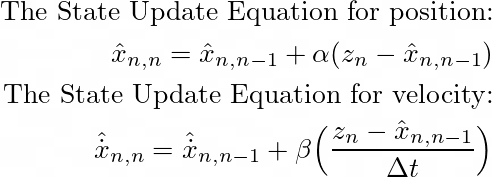
在真实的卡尔曼滤波器中,α 和 β 都被卡尔曼增益取代,卡尔曼增益在每次迭代时计算。在此示例中,我们选择了值,但在接下来的文章中,我们将学习如何计算卡尔曼增益。现在,让我们看一个实际的例子。
七、数值例子
回顾一下,自动赛车正在远离天线,天线每隔 Δ t = 2 秒通过信号强度测量距离。关于参数,我们将使用 α = 0.2 和 β = 0.1。
1) t = 0
初始化:赛车在以下条件下启动
![]()
2) t = 1
此时,我们根据之前的初始化来计算第一个预测。t = 0时的值为:
![]()
步骤 1 - 预测:现在我们可以根据t = 1计算预测。应使用状态外推方程将第一个猜测外推到第一个周期:

这意味着赛车在第一次测量中移动了 110 m,而其匀速使其保持相同的 55 m/s。
![]()
步骤 2 — 更新:假设天线测量值为z₁ = 89 m。然后我们使用状态更新方程计算当前距离:
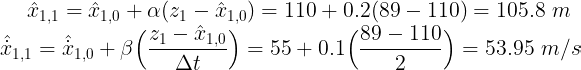
3) t = 2
步骤 1 — 预测:使用状态外推方程进行下一个状态估计:
![]()

第 2 步 — 测量:假设天线测量为
![]()
第 3 步 — 更新:状态更新方程:
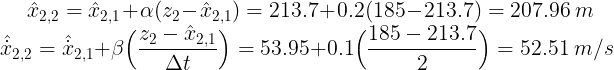
4) t = 3
预测、测量和更新

5) t = 4
预测、测量和更新
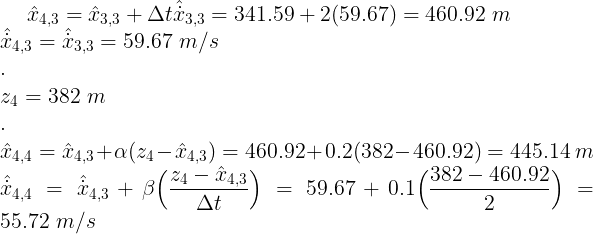
6) t = 5
预测、测量和更新
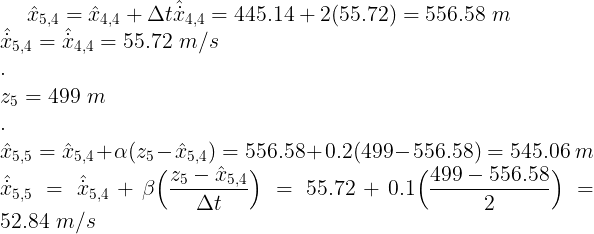
7) t = 6
预测、测量和更新

8) t = 7
预测、测量和更新

9) t = 8
预测、测量和更新
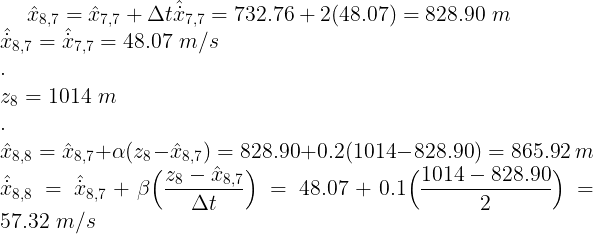
10) t = 9
预测、测量和更新
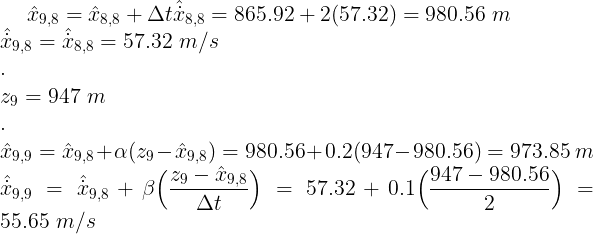
11) t = 10
预测、测量和更新
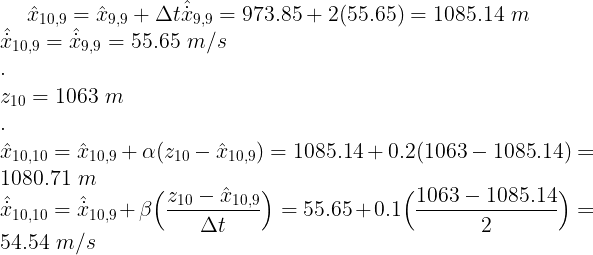
下表总结了每次迭代的值:

在下图中,我们可以看到估计(黄色)值如何接近地面实况,即真实值(恒定速度可以更轻松地估计赛车随时间的进展情况)。我们可以看到天线测量值(红色)变化很大,并且预测(蓝色)对这种变化做出“反应”,正如我们从 14 秒到 16 秒看到的那样。在 16 秒时,系统预测汽车将接近 800 m,因为在 14 秒时计算的速度表明汽车将以 50.55 m/s 的速度移动。然而,通过天线测量和预测结果,更新步骤可以正确估计汽车的位置(在 16 秒时更接近地面实况)。估计(黄色)保持不变,几乎模仿了真实情况(绿色)。

但是如果我们将 α 和 β 值分别更改为 0.8 和 0.4 会怎样?在这种情况下,在两个状态更新方程(距离和速度)中,我们将更加信任测量结果,并且“平滑”程度要低得多。结果是估计和预测将会有更大的差异,如下图所示。比较预测线(蓝色)和估计线(黄色)很有趣。在 8 秒时,系统预测汽车与天线的距离将更远,接近 600 m(因为在 6 秒时,天线测量值与 4 秒时的测量值相比“高”,这意味着汽车会增加它的速度)。然而,在 8 秒进行测量后,系统会考虑预测值和测量值来估计汽车的当前距离,该距离比预测值更接近地面实况。同样的推理适用于14 s ~ 18 s 时段。
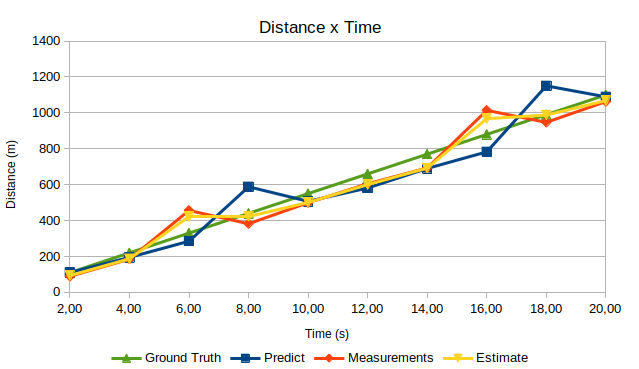
根据这两个图表,您可能想知道我们是否应该始终对 α 和 β 使用较低的值。然而,值得一提的是,这些值取决于测量精度。使用高精度硬件时,建议使用较高的 α 和 β 值,因为预测和估计应遵循传感器进行的精确测量。相反,当使用测量结果不一致的劣质传感器时,α 和 β 的值应该较低,并且滤波器将平滑测量中的不确定性。
八、总结
在这一部分中,我们从两个问题陈述开始,并建立了对卡尔曼滤波器的直观理解。然后我们正式引入了Alpha-Beta滤波器,它构成了卡尔曼滤波器的基础。
以下是一些注意事项:
— 使用Alpha-Beta 过滤器,我们不会忽略错误/噪声(这不会映射到现实生活中的问题),而是会考虑错误/噪声/不一致来计算估计;
—在过滤器需求分析中选择 alpha 和 beta 的值。过滤器是经过设计的,而不是临时选择的。这同样适用于对系统进行“建模”的状态外推方程;
—充分理解问题对于设计滤波器很重要;
— 如前所述,状态预测和状态更新步骤对于良好的估计都至关重要。
现在我们已经很好地理解了这些概念,我们将在下一部分中正式讨论贝叶斯滤波器和卡尔曼滤波器。马蒂亚斯·曼泰利