一、介绍

对于优化问题，贪心算法总是做出当前看起来最好的选择，并将其添加到当前的子解中
最优子结构:剩余的子问题$P^{\prime }$与原问题$P$具有相同的形式，且$P^{\prime }$的最优解继承自$P$
与动态规划不同，动态规划列出所有情况的最优解再进行判断，而贪心算法没有判断，它的最优解基于上一个的最优解，因此必须要决定子问题的最优解。
因此这类问题必须验证每一次求解时最优解就是上一个子问题最优解得出的。
记住不是所有问题都有最优贪心解，需要去证明它

二、分数背包问题

问题描述

大体与0-1背包一样，不一样的地方在于0-1背包中商品是一个整体，而分数背包商品可分，因此不存在填不满的情况。

分析

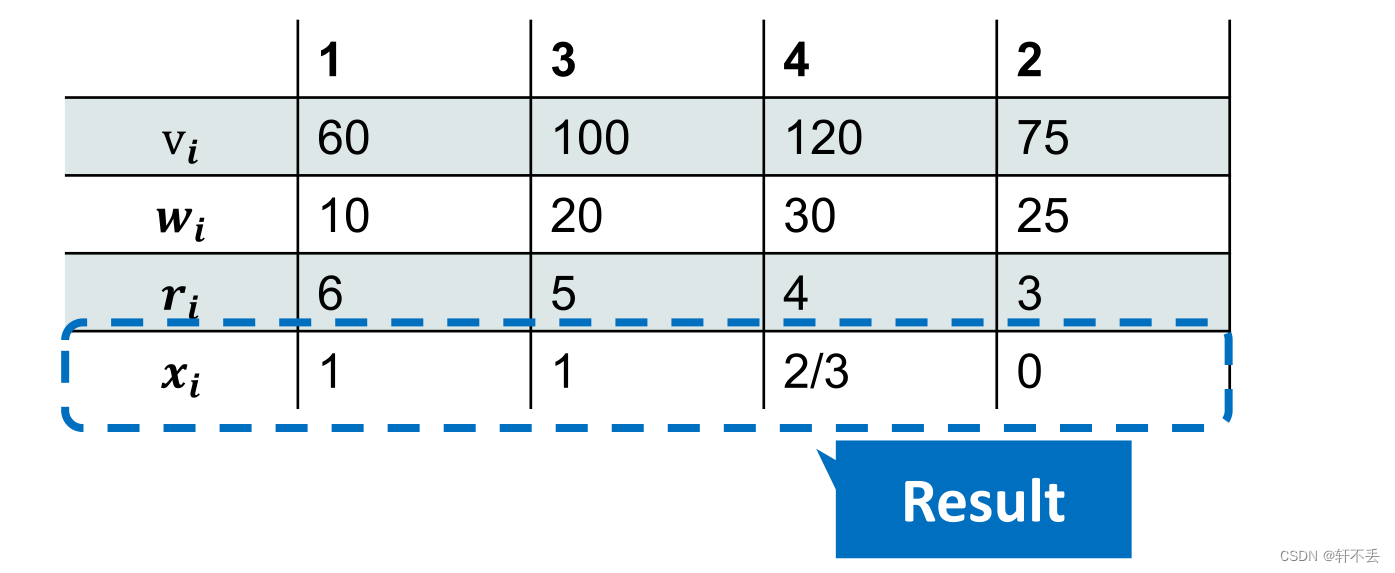
首先计算每件商品单位重量的价值：$p_i=\frac{v_i}{w_i}$ $fori=1,2,...,n$

因为需要价值最大，因此需要按照单价降序排列，让排序后的项目序列为$1、2、\dots 、i、\dots 、n$，对应的每磅值和权重分别是$p_i$和$w_i$
设k为当前权值限制，每次迭代，都按照上述排列选择最大价值且未被选择的
    if $k\ge w_i$，则$x_i$全部都需要被选择，令$k=k-w_i$，考虑下一个商品
    if $k<w_i$，则$x_i=\frac{k}{w_i}$需要被选择，算法终止

时间复杂度

排序最快时间复杂度为$O(nlogn)$，而计算价值只需要一层循环直到k为0为止，因此时间复杂度小于$O(k)$，因此整体时间复杂度$T(n)=O(nlogn)$

伪代码

Fraction-Knapsack(n,v,w,k)
for i ← 1 to n do
	r[i] ← v[i]/w[i]
	x[i] ← 0
end

sort the item in decreasing order

j ← 0
while K>0 and j <= n do
	j ← j+1
	if K>w[j] then
		 x[j] ← 1
		 K ← K-w[j]
	end
	else
		x[j] ← k/w[j]
	end
end
return xi

案例

彩蛋

0-1背包问题没有贪心解，每次都选择最佳的，最后不一定是最优解

三、活动选择问题

问题描述

$有很多活动，每个活动在不同的时间开始或结束，目标是为了参加尽可能多的活动$

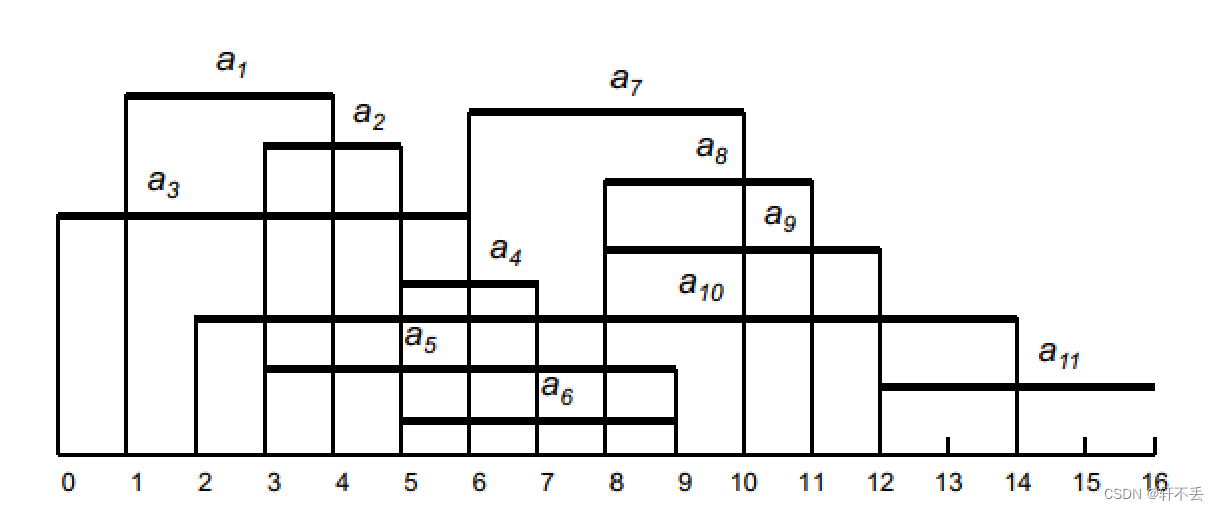
活动时间会有重叠，因此所要做的是选择最多数量的不重叠的活动

分析

每次选择一个，怎么选择可以导致据局部最优，每次选择完毕后，我们需要留更多的时间让剩下的活动有更充足空间，这样选择才是最优的，因此我们每次应该选择最早结束的那个。

一旦做出选择，删除所有不兼容的活动（即与所选活动重叠）

对剩余的活动重复算法

伪代码

Greedy-Activity-Selection(A)
Sort activities in increasing order of finishing time
P ← a1
k ← 1
for i ← 2 to n do
	if s[i]>= f[k] then
		p ← p U ai
		k ← i
	end
end
return P

时间复杂度

只有一个循环，之间复杂度是$O(n)$，排序时间复杂度是$O(nlogn)$，因此总的时间复杂度$T(n)=O(nlogn)$

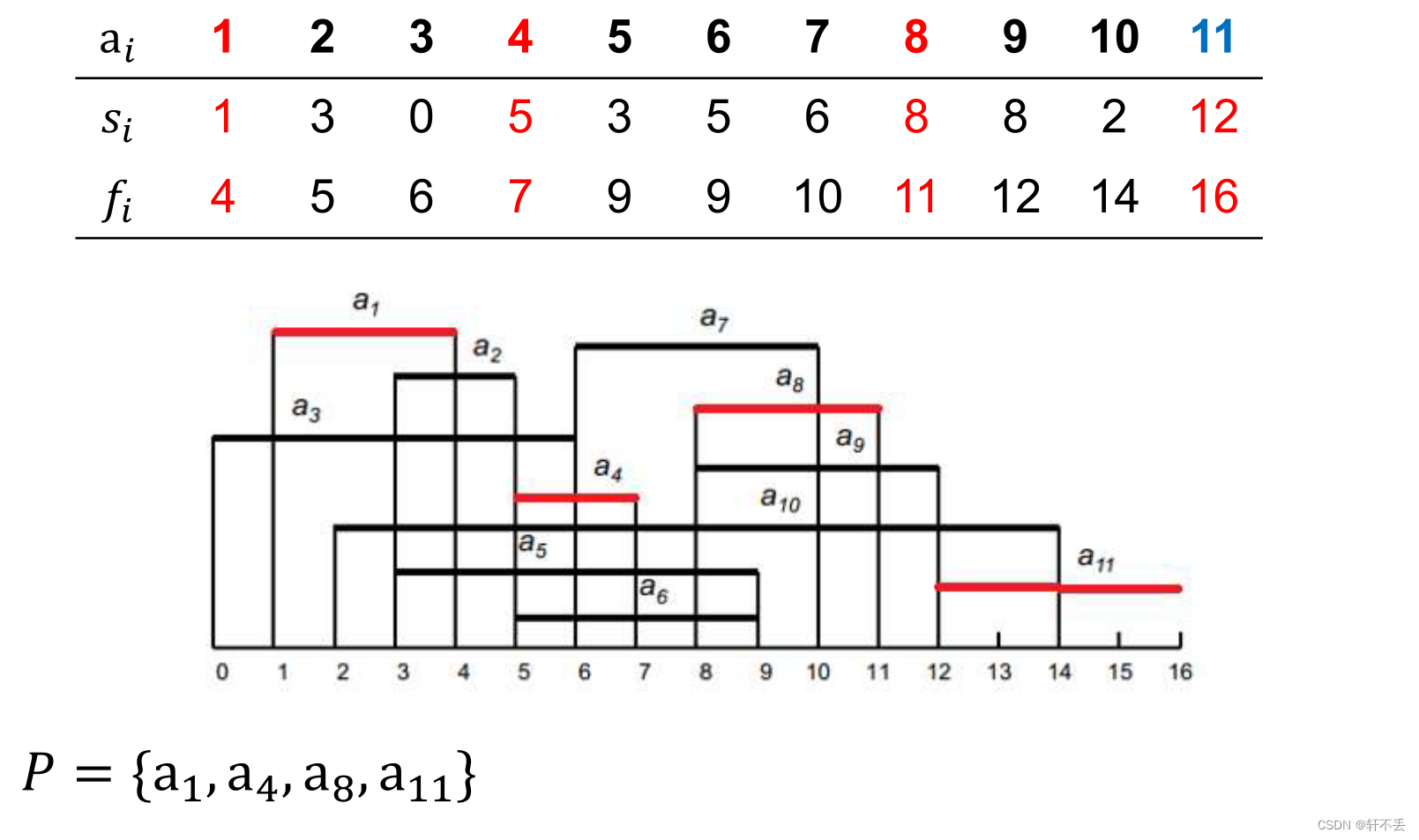
拓展：加权活动选择

$每个活动都增加权重，现在的目标找到相互兼容的活动的最大加权子集$

分析

再用上述思路就不行了，有可能某个权重特别高，就不能选择个数多的了。
如下图：

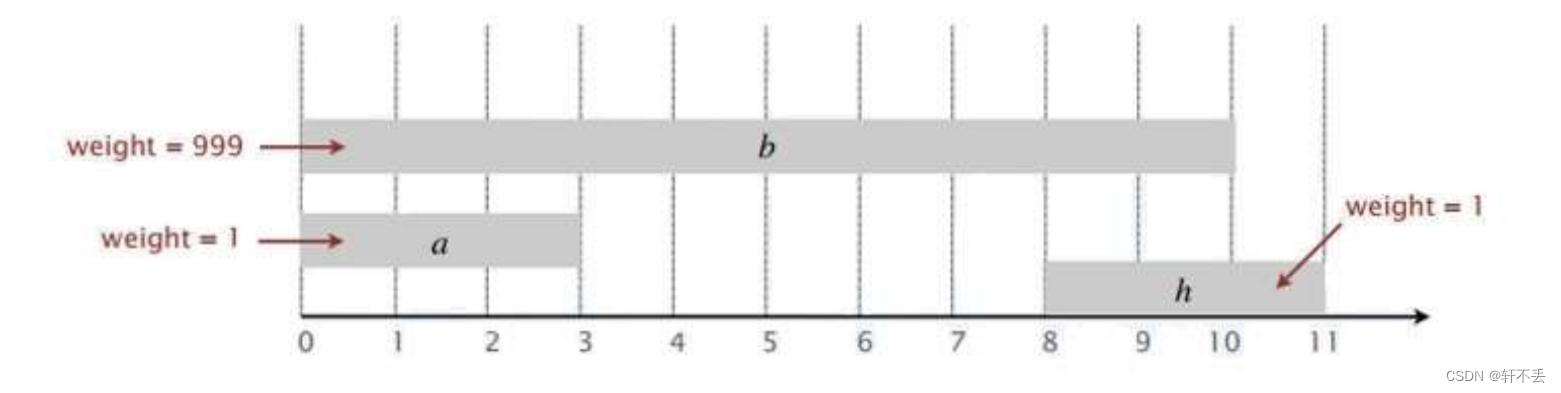
事实上，涉及到加权的都无法用贪心算法去计算，因为无法验证前一个解是否是最优解。加权最优解我们最常用的解决方法就是动态规划。
设计到状态转移，我们应该指定一个顺序，与无加权的动态规划一样按照结束时间排序。

计算

将活动按照结束时间从小到大排序，记为$a_1,a_2...a_j$

定义$OPT(j)$为$a_1,a_2...a_j$这些活动的最大加权值。$P(j)$为最大的$i$，使得$a_i$与$a_j$时间活动不重叠。

目标：计算$OPT(n)$的最大值

边界：$OPT(0)=0$

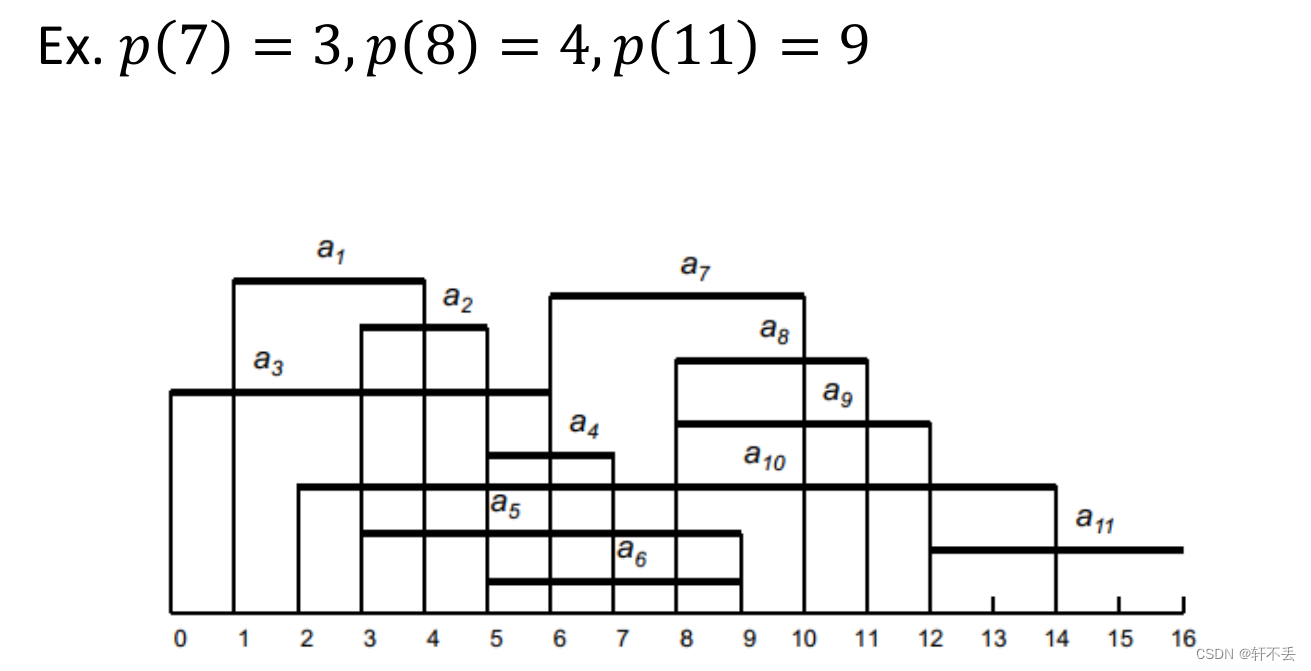
$p(j)$可以很简单利用二分法去计算。
根据上述分析，列出状态方程
$OPT(j)=\{\begin{array}{ll}0& ifj=0\\ max(OPT(j-1),w_i+OPT(p(j)))& ifx>0\end{array}$

伪代码

sort and get a1,a2,...,an
compute p[1],p[2],...,p[n]
OPT(0) ← 0
for j =1 to n do
	OPT(j) ← max{OPT(j-1),wj+OPT(p[j])}
end
return OPT(n)

时间复杂度

排序$O(nlogn)$，计算$p(j)$采用二分法$O(nlogn)$，循环$O(n)$，因此总体时间复杂度$T(n)=O(nlogn)$

案例

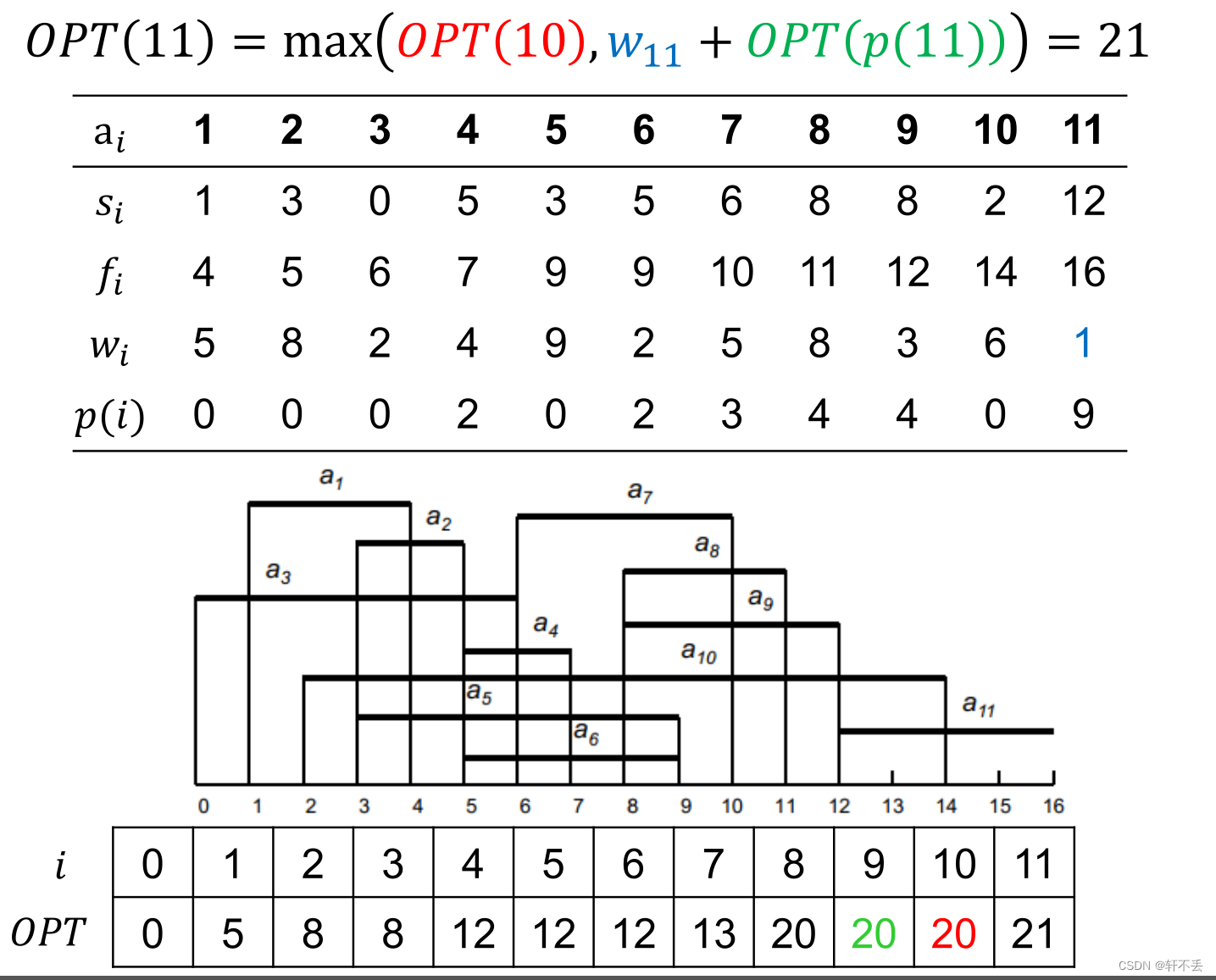
对比动态规划和贪心算法

贪心算法从不考虑自己的选择，总是关注现在。

动态规划基于之前的决定，记录历史进行改变。

四、哈夫曼编码

将字符串变成二进制编码形式，但是需要这样一个编码，使得每个消息都是唯一可解码的，这样才能具有唯一可破译性。

分类

定长编码

每个码字都有相同的长度。因为是固定长度，所以肯定是唯一可破译的，不可能会有歧义。

目标

为了让转换为二进制串占有内存最小，我们需要让出现频率高的字符转换的码字长度小

变长码

每个码字有不同的长度。

根据字符串每个字符出现的频率采取不同编码长度，这样使用的Bit位比定长编码效率高。但是变长码可能出现歧义，因此要找到唯一可破译的解决方法。

我们定义前缀自由码：如果一个代码没有一个码字是另一个码字的前缀。每个由前缀自由码编码的消息都是唯一可破译的。
由于没有任何码字是其他码字的前缀，我们总是可以在消息中找到第一个码字，剥离它，并继续解码。

案例

下图可以看出，叶子节点和字符1-1对应（这样就能保持唯一可解码的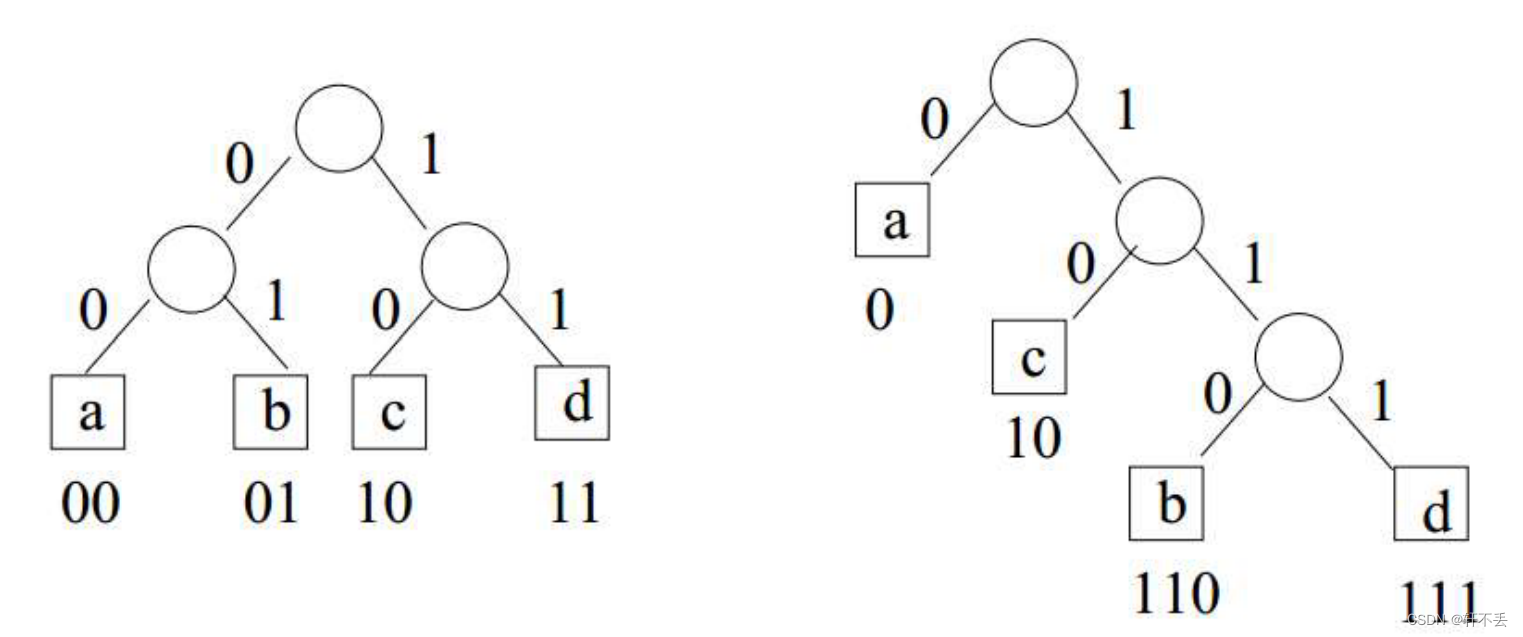）从根节点到叶节点的路径上的二进制字符串是与叶节点上的字符相关联的码字。
叶子$a_i$的深度$d(a_i)$等于与该叶子相关的码字的长度$L(c(a_i))$
哈夫曼编码问题等价于最小加权外路径长度问题：以下公式即求最小加权路径长度
${\sum }_{i=1}^{n}f(a_i)d(a_i)={\sum }_{i=1}^{n}f(a_i)L(c(a_i))$
$f(a_i)为第a_i个叶子出现频率$

分析

$$\begin{gathered} 从字符串A中选出两个频率最小的字符x,y。 \\ 创建一个以这两个字符作为叶子的子树。 \\ 将这个子树的根标记为z \\ 设频率f(z)=f(x)+f(y) \\ 去除x，y加上z，形成一个新的字母a^{\prime }。 \\ 重复这个过程，称为合并，与新的字母A^{\prime }，直到一个字母只剩下一个符号。 \\ 生成的树是哈夫曼代码。 \\ 给定频率分布的最优(最小代价)前缀码。 \end{gathered}$$

伪代码

利用优先队列（堆）去维护树，以频率最为关键字。

Huffman(A)
for i ← 1 to n-1 do
	z ← a new code
	z.left ← Extract-Min(Q);
	z.right ← Extract-Min(Q);
	z.freq ← z.left.freq+z.right.freq;
	Insert(Q,z)
end
return Extract-Min(Q);

时间复杂度

每个优先队列操作（最小堆的更新）需要花费$O(logn)$时间，循环$n次$，因此时间复杂度$T(n)=O(nlogn)$

彩蛋-dangling suffix

唯一可译码的判决算法实现。(即判断一个编码是否是可译码)