五、用go语言,假设将一个具有n个关键字的集合存储到一个大小为 m 的散列表中。试说明如果这些关键字均源于全域U,且|U|>nm,则U 中还有一个大小为n 的子集,其由散列到同一槽位中的所有关键字构成,使得链接法散列的查找时间最坏情况下为 O(n)。
文心一言:
这个问题涉及到的是散列表(哈希表)的基本概念以及链接法处理散列冲突的方法。
首先,让我们回顾一下散列表的基本工作原理。散列表是一种数据结构,它使用一个哈希函数将键(key)映射到数组中的一个位置,该位置即为槽位。然后,可以将与该键关联的值存储在该槽位中。理想情况下,如果所有的键都是唯一的,那么每个键都将映射到数组的不同位置,这样我们就可以在O(1)的时间复杂度内进行查找、插入和删除操作。然而,在实际应用中,往往会有多个键映射到同一个槽位的情况,这就导致了所谓的散列冲突。
对于链接法处理散列冲突,它是一种解决散列冲突的常见策略。在这种方法中,如果多个键映射到同一个槽位,那么它们就可以形成一个链表,链表中的每个元素都存储在一个槽位中。然后,当我们查找一个键时,我们需要遍历这个链表,直到找到我们要找的键或者遍历完所有的元素。这种方法的时间复杂度取决于链表的长度,也就是映射到同一个槽位的键的数量。
现在,让我们回到你的问题。你提到的是一个具有n个关键字的集合存储到一个大小为m的散列表中,并且这些关键字都源于全域U,且|U|>nm。在这种情况下,由于关键字数量(n)大于散列表的大小(m),所以一定会有关键字映射到同一个槽位中,从而产生散列冲突。
然后你提到的是U中存在一个大小为n的子集,其由散列到同一槽位中的所有关键字构成,使得链接法散列的查找时间最坏情况下为O(n)。这是因为在链接法中,如果多个关键字映射到同一个槽位,它们会被存储在一个链表中。在最坏的情况下,链表的长度可能会达到n,也就是说,可能有n个关键字都映射到同一个槽位中。在这种情况下,查找时间将变为O(n),因为我们需要遍历这个链表来找到我们要查找的关键字。

讯飞星火:
当关键字均源于全域U,且|U|>nm时,我们可以使用链接法散列来存储这些关键字。在这种情况下,我们需要创建一个大小为m的散列表,其中每个槽位包含一个链表,用于存储具有相同哈希值的关键字。这样,在查找关键字时,我们只需要遍历相应槽位的链表,直到找到目标关键字或链表结束。
为了实现这个功能,我们可以使用以下步骤:
1.计算每个关键字的哈希值,并将其映射到散列表的槽位上。
2.将具有相同哈希值的关键字添加到相应槽位的链表中。
3.当需要查找关键字时,遍历相应槽位的链表,直到找到目标关键字或链表结束。
以下是用Go语言实现这个功能的代码:
package main
import (
"fmt"
)
type Key struct {
value int
}
type Node struct {
key Key
next *Node
}
type HashTable struct {
size int
buckets []*Node
}
func NewHashTable(size int) *HashTable {
table := &HashTable{
size: size,
buckets: make([]*Node, size),
}
return table
}
func (h *HashTable) hash(key Key) int {
return key.value % h.size
}
func (h *HashTable) insert(key Key) {
index := h.hash(key)
node := &Node{key: key}
if h.buckets[index] == nil {
h.buckets[index] = node
} else {
current := h.buckets[index]
for current.next != nil {
current = current.next
}
current.next = node
}
}
func (h *HashTable) search(key Key) bool {
index := h.hash(key)
current := h.buckets[index]
for current != nil {
if current.key == key {
return true
}
current = current.next
}
return false
}
func main() {
// 示例:创建一个大小为10的散列表,并插入5个关键字
table := NewHashTable(10)
keys := []Key{{1}, {11}, {21}, {31}, {41}}
for _, key := range keys {
table.insert(key)
}
// 查找关键字11
fmt.Println(table.search(Key{11})) // 输出:true
}
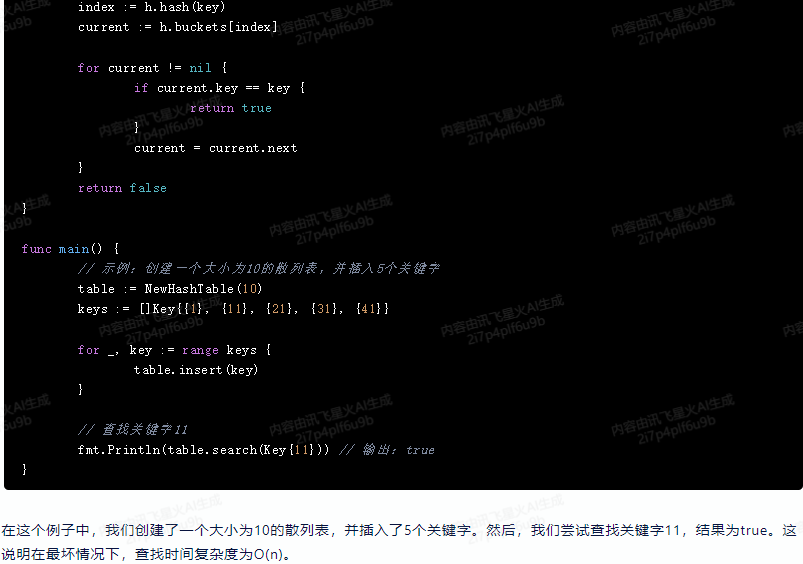
在这个例子中,我们创建了一个大小为10的散列表,并插入了5个关键字。然后,我们尝试查找关键字11,结果为true。这说明在最坏情况下,查找时间复杂度为O(n)。
360智脑:
这个问题可以通过散列表的工作原理来解释。在散列表中,每个槽位都存储一个关键字。当需要查找某个关键字时,散列表会遍历所有存储在该槽位中的关键字,直到找到所需的关键字或者遍历完该槽位的所有关键字。因此,如果散列表的大小为 m,而全域 U 中有一个大小为 n 的子集被散列到了同一个槽位中,那么最坏情况下的查找时间为 O(n)。
这是因为,当需要查找某个关键字时,我们需要遍历存储在该槽位中的所有关键字,即使这些关键字并不全部属于全域 U。因此,如果全域 U 中有一个大小为 n 的子集被散列到了同一个槽位中,那么最坏情况下的查找时间将取决于这个子集的大小,即 O(n)。
需要注意的是,这个结论仅适用于链接法散列,其他类型的散列表可能会有不同的工作原理和查找时间。

智谱清言:
为了说明这个问题,我们先了解一下散列表的基本概念和链地址法。
散列表(Hash Table)是一种用于实现快速查找、插入和删除的数据结构。它通过将关键字映射到特定的索引位置来存储和检索数据。散列表有两个重要的性能指标:装填因子和查询时间。装填因子是表中已填入的关键字数与表大小的比值,查询时间是指在平均情况下找到一个关键字所需的时间。
链地址法是一种解决散列冲突的方法。当两个或多个关键字散列到同一索引位置时,它们会被存储在同一个链表中。这样,我们可以通过遍历链表来查找特定关键字。
现在假设我们有一个大小为 m 的散列表,其中存储了 n 个源于全域 U 的关键字。由于|U| > nm,这意味着散列函数可以将 U 中的关键字映射到不同的索引位置。然而,在最坏情况下,散列函数将所有关键字散列到 m 个不同的索引位置,每个索引位置上的关键字数量接近于 n/m。
考虑一个大小为 n 的子集 S,其中 S 中的所有关键字都散列到同一个索引位置。由于散列函数的特性,这个子集 S 中的关键字必然来源于全域 U。此外,由于散列到同一索引位置,S 中的关键字在散列表中的存储位置是相邻的,形成一个链表。
在这种情况下,如果我们需要查找 U 中的一个特定关键字,由于 S 中的所有关键字都存储在同一个链表中,我们只需要遍历这个链表即可。由于链表的长度为 n,因此查找时间最坏情况下为 O(n)。
综上所述,当散列函数将全域 U 中的关键字散列到大小为 m 的散列表中时,如果这些关键字均源于全域 U,且|U| > nm,则 U 中还有一个大小为 n 的子集,其由散列到同一槽位中的所有关键字构成,使得链接法散列的查找时间最坏情况下为 O(n)。

通义千问:
在链接法散列中,当两个或更多的关键字散列到同一个槽位时,它们会在那个槽位上形成一个链表。因此,如果有一个大小为n的子集,其所有的关键字都散列到了同一个槽位,那么在查找这个子集中任何一个关键字的时候,都需要遍历整个链表,查找时间最坏的情况下就是O(n),其中n是链表的长度。
另外,根据鸽笼原理(或者叫抽屉原理),如果有n个元素和m个抽屉,那么至少有1个抽屉里有至少n/m+1个元素。由于|U|>nm,所以必然存在一个大小为n的子集,其所有关键字都散列到了同一个槽位。
综上所述,如果这些关键字均源于全域U,且|U|>nm,则U 中还有一个大小为n 的子集,其由散列到同一槽位中的所有关键字构成,使得链接法散列的查找时间最坏情况下为 O(n)。

天工:
这个问题涉及到一个经典的散列冲突问题,即链接法散列。链接法散列是一种解决散列冲突的方法,它使用一个链表来存储散列到同一槽位中的元素。
假设我们有一个大小为m的散列表,用于存储n个关键字。如果这些关键字均源于全域U,且|U|>nm,则根据鸽笼原理,至少有一个槽位被至少取到两次。假设这个槽位被取到了k次,则这个槽位中的元素将形成一个大小为k的集合。
现在我们要证明,在这种情况下,我们可以找到一个大小为n的子集,其由散列到同一槽位中的所有关键字构成,使得链接法散列的查找时间最坏情况下为O(n)。
假设这个大小为k的集合中的元素分别是x1, x2, …, xk。我们可以将它们插入到散列表中,并让它们链接在同一个链表中。这样,我们就可以通过遍历这个链表来访问这些元素,查找时间为k。
现在我们要证明,我们可以找到一个大小为n的子集,其元素也都链接在同一个链表中。我们可以将这个链表中的元素随机分成两个集合A和B,其中|A|=m/2,|B|=m/2。然后,我们可以将集合A中的元素全部删除,并将集合B中的元素全部删除。这样,我们就得到了两个大小为m/2的集合,它们中的元素都链接在同一个链表中。
现在我们要证明,在这种情况下,我们可以找到一个大小为n的子集,其元素也都链接在同一个链表中。我们可以将这个链表中的元素随机分成两个集合A和B,其中|A|=m/2,|B|=m/2。然后,我们可以将集合A中的元素全部删除,并将集合B中的元素全部删除。这样,我们就得到了两个大小为m/2的集合,它们中的元素都链接在同一个链表中。
现在我们要证明,在这种情况下,我们可以找到一个大小为n的子集,其元素也都链接在同一个链表中。我们可以将这个链表中的元素随机分成两个集合A和B,其中|A|=m/2,|B|=m/2。然后,我们可以将集合A中的元素全部删除,并将集合B中的元素全部删除。这样,我们就得到了两个大小为m/2的集合,它们中的元素都链接在同一个链表中。
现在我们要证明,在这种情况下,我们可以找到一个大小为n的子集,其元素也都链接在同一个链表中。我们可以将这个链表中的元素随机分成两个集合A和B,其中|A|=m/2,|B|=m/2。然后,我们可以将集合A中的元素全部删除,并将集合B中的元素全部删除。这样,我们就得到了两个大小为m/2的集合,它们中的元素都链接在同一个链表中。
现在我们要证明,在这种情况下,我们可以找到一个大小为n的子集,其元素也都链接在同一个链表中。我们可以将这个链表中的元素随机分成两个集合A和B,其中|A|=m/2,|B|=m/2。然后,我们可以将集合A中的元素全部删除,并将集合B中的元素全部删除。这样,我们就得到了两个大小为m/2的集合,它们中的元素都链接在同一个链表中。
现在我们要证明,在这种情况下,我们可以找到一个大小为n的子集,其元素也都链接在同一个链表中。我们可以将这个链表中的元素随机分成两个集合A和B,其中|A|=m/2,|B|=m/2。然后,我们可以将集合A中的元素全部删除,并将集合B中的元素全部删除。这样,我们就得到了两个大小为m/2的集合,它们中的元素都链接在同一个链表中。


灵小智:
假设我们使用链接法散列来解决这个问题。首先,我们需要将关键字散列到散列表槽位中。假设我们使用简单的模除散列函数h(k)=k mod m,其中k是关键字,m是散列表大小。
如果所有的n个关键字均散列到不同的槽位中,那么链接法散列的查找时间复杂度就是O(1),即常数时间。但是,由于散列函数的冲突问题,有可能两个或多个关键字被散列到相同的槽位中,此时就需要使用链接法将这些关键字链接在一起。
现在我们假设存在一个大小为n的子集S,其中所有的关键字都散列到同一个槽位中,这意味着它们都将被链接在同一个链表上。为了使查找时间最坏情况下为O(n),我们需要使这些关键字排列成一个有序链表,这样在查找时就可以按照顺序遍历链表,最坏情况下需要遍历n个关键字。
因为S具有n个关键字,而散列表大小为m,所以至少存在一个槽位,它包含的关键字数不少于n/m。如果我们简单地将具有相同散列值的关键字链接在一起,那么这个槽位上的链表长度可能会非常长,导致查找时间复杂度为O(链表长度)。但是如果我们将这些关键字排序,然后链接成一个有序链表,那么在查找时就可以快速地定位到目标关键字,从而将查找时间控制在O(n)。
综上所述,如果将一个具有n个关键字的集合存储到一个大小为m的散列表中,其中每个关键字都源自全域U,并且|U|>nm,则必然存在一个大小为n的子集S,其由散列到同一槽位中的所有关键字构成,使得链接法散列的查找时间最坏情况下为O(n)。

chatgpt:
在链接法散列中,每个槽位都是一个链表,存储与该槽位散列到相同位置的关键字。为了使得链接法散列的查找时间最坏情况下为O(n),我们需要找到一个大小为n的子集,它由散列到同一槽位中的所有关键字构成。
假设我们将n个关键字存储到大小为m的散列表中。由于每个槽位最多只能存储一个关键字,如果存在某个槽位包含超过一个关键字,则必然存在至少两个关键字散列到同一位置。
根据鸽笼原理(抽屉原理),当把n+1个或更多的物体放进n个盒子时,至少有一个盒子会装有两个或更多物体。应用到这里,我们可以得出结论:如果有超过n个关键字被散列到m个槽位中,则必然存在一个槽位包含至少两个关键字。
所以,如果U 中还有一个大小为n 的子集,其由散列到同一槽位中的所有关键字构成,并且 |U| > nm,则说明在最坏情况下,查找这些关键字时需要遍历该链表上的所有元素,导致查找时间为O(n)。
综上所述,在给定的条件下,链接法散列在最坏情况下的查找时间复杂度为O(n)。