分类目录:《深入理解强化学习》总目录
我们在《深入理解强化学习——多臂赌博机》系列文章中介绍了几种平衡试探和开发的简单方法。 ϵ − \epsilon- ϵ−贪心方法在一小段时间内进行随机的动作选择,而UCB方法虽然采用确定的动作选择,却可以通过在每个时刻对那些具有较少样本的动作进行优先选择来实现试探。梯度赌博机算法则不估计动作价值,而是利用偏好函数,使用Softmax分布来以一种分级的、概率式的方式选择更优的动作。简单地将收益的初值进行乐观的设置,就可以让贪心方法也能进行显式试探。
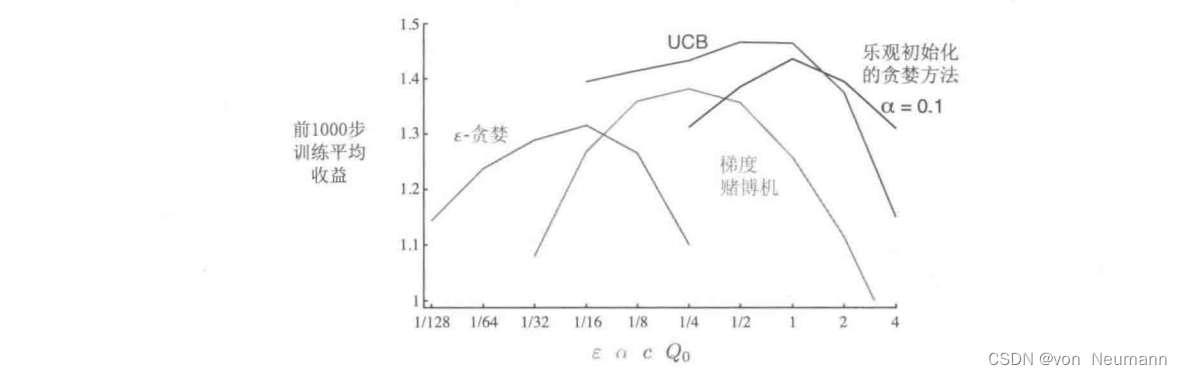
很自然地,我们会问哪种方法最好。尽管这是一个很难回答的问题,但我们可以在10臂测试平台上运行它们,并比较它们的性能。一个难题是它们都有一个参数,为了进行一个有意义的比较,我们将把它们的性能看作关于它们参数的一个函数。到目前为止,我们的图表已经分别给出了每种算法及参数随时间推移的学习曲线。但如果我们把所有算法的所有参数对应的学习曲线全部画在一起,就会过于复杂,造成视觉上的混乱。所以我们总结了一个完整的精简的学习曲线,展示了每种算法和参数超过1000步的平均收益值,这个值与学习曲线下的面积成正比。下图显示了《深入理解强化学习——多臂赌博机》系列文章中各种赌博机算法的性能曲线,每条算法性能曲线都被看作一个自己参数的数,
x
x
x轴用单一的尺度显示了所有的参数。这种类型的图称为参数研究图。需要注意的是,轴上参数值的变化是2的倍数,并以对数坐标表示。由图可见,每个算法性能曲线呈倒U形;所有算法在其参数的中间值处表现最好,既不太大也不太小。在评估一种方法时,我们不仅要关注它在最佳参数设置上的表现,还要注意它对参数值的敏感性。所有这些算法都是相当不敏感的,它们在一系列的参数值上表现得很好,这些参数值的大小是一个数量级的。总的来说,在这个问题上,UCB似乎表现最好。
尽管《深入理解强化学习——多臂赌博机》系列文章中提出的方法很简单,但在我们看来,它们被公认为是最先进的技术。虽然有更复杂的方法,但它们的复杂性和假设使它们在我们真正关注的完整强化学习问题中并不适用。
虽然本系列文章探讨的简单方法可能是目前让我们能做到最好的方法,但它们还远远不能解决平衡试探和开发的问题。在多臂赌博机问题中,平衡试探和开发的一个经典解决方案是计算一个名为Git.tins指数的特殊函数。这为一些赌博机问题提供了一个最优的解决方案,比在本系列文章中讨论的方法更具有一般性,但前提是已知可能问题的先验分布。不幸的是,这种方法的理论和可计算性都不能推广到我们在本书中探讨的完整强化学习问题。
贝叶斯方法假定已知动作价值的初始分布,然后在每步之后更新分布(假定真实的动作价值是平稳的)。一般来说,更新计算可能非常复杂,但对于某些特殊分布(称为共轭先验)则很容易。这样,我们就可以根据动作价值的后验概率,在每一步中选择最优的动作。这种方法,有时称为后验采样或汤普森采样(Thompson Sampling),通常与我们在本系列文章中提出的最好的无分布方法性能相近。
贝叶斯方法甚至可以计算出试探和开发之间的最佳平衡。对于任何可能的动作,我们都可以计算出它对应的即时收益的分布,以及相应的动作价值的后验分布。这种不断变化的分布成为问题的信息状态。假设问题的视界有1000步,则可以考虑所有可能的动作,所有可能的收益,所有可能的下一个动作,所有下一个收益等等,依此类推到全部1000步。有了这些假设,可以确定每个可能的事件链的收益和概率,并且只需挑选最好的。但可能性树会生长得非常快,即使只有两种动作和两种收益,树也会有22000个叶子节点。完全精确地进行这种庞大的计算通常是不现实的,但可能可以有效地近似。贝叶斯方法有效地将赌博机问题转变为完整强化学习问题的一个实例。最后,我们可以使用近似强化学习方法来逼近最优解。
参考文献:
[1] 张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 人民邮电出版社, 2022.
[2] Richard S. Sutton, Andrew G. Barto. 强化学习(第2版)[M]. 电子工业出版社, 2019
[3] Maxim Lapan. 深度强化学习实践(原书第2版)[M]. 北京华章图文信息有限公司, 2021
[4] 王琦, 杨毅远, 江季. Easy RL:强化学习教程 [M]. 人民邮电出版社, 2022