【C++笔记】二叉搜索树的模拟实现

news2024/11/18 21:27:56

【C++笔记】二叉搜索树的模拟实现

  • 一、二叉搜索树的概念
  • 二、二叉搜索树的模拟实现
    • 2.0、定义二叉树节点
    • 2.1、非递归接口实现
      • 2.1.1、插入
      • 2.1.2、查找
      • 2.1.3、删除
    • 2.2、递归接口实现
      • 2.2.1、插入
      • 2.2.2、查找
      • 2.2.3、删除
  • 三、升级为K-V模型

一、二叉搜索树的概念

二叉搜索树的概念：

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

就比如下面这一棵树就是一颗二叉搜索树：
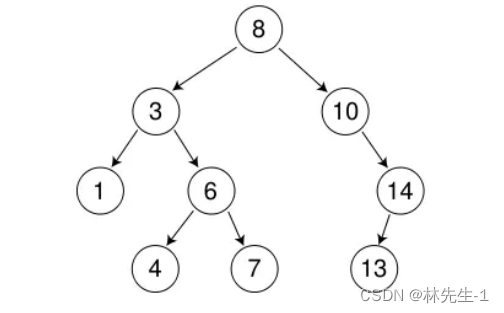
在这里插入图片描述
学习二叉搜索树其实也是为了后面学习AVL树和红黑树打下基础，因为AVL树和红黑树都是有二叉搜索树延伸出来的。

基于二叉搜索树的的特性，如果要在二叉搜索树中查找某一个数，最多只需要查找到最底层(如果比根大就去右子树去查找，如果比根小就去左子树中查找)，很容易得出查找的时间复杂度为logn。所以在应用中二叉搜索树也常常用于查找。

但是二叉搜索树查找的时间复杂度也并非一直稳定在logn，如果是一些比较特殊的树，时间复杂度可能会升到n，就比如下面这棵树：
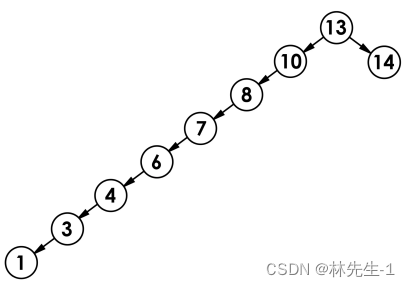
在这里插入图片描述
所以AVL树和红黑树就是为了解决二叉搜索树的这个缺陷而设计出来的。

而且我们后面要学到的set和map就是用红黑树封装出来的，所以学好二叉搜索树也就变成了基础中的基础。

二、二叉搜索树的模拟实现

2.0、定义二叉树节点

搜索二叉树的节点其实也和传统的二叉树节点一样，只是我们处理这些节点的规则变了而已：

// 搜索二叉树节点
template <class K>
struct BSTreeNode {
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _val;
	BSTreeNode(const K& val)
		:_left(nullptr)
		, _right(nullptr)
		, _val(val)
	{}
};

然后我们在搜索二叉树的类中就只需要封装一个根节点的指针即可：

template <class K>
class BSTree {
public :
	typedef BSTreeNode<K> Node;
	// ……
private :
	Node* _root = nullptr;
};

2.1、非递归接口实现

因为搜索二叉树可以说是为了应用而产生的，所以它主要的接口不多，只需要实现三个：插入、查找、删除即可。其他的一些接口和普通二叉树是一样的。

2.1.1、插入

根据二叉搜索输的规则，我们很容易就能想出插入该怎么写：
我们只需要从根节点出发，一直遍历，如果要插入的节点比当前节点小那我们就往左子树走，如果如果比当前节点大就往右子树走，知道当前节点cur走到空就确定了要插入的位置：
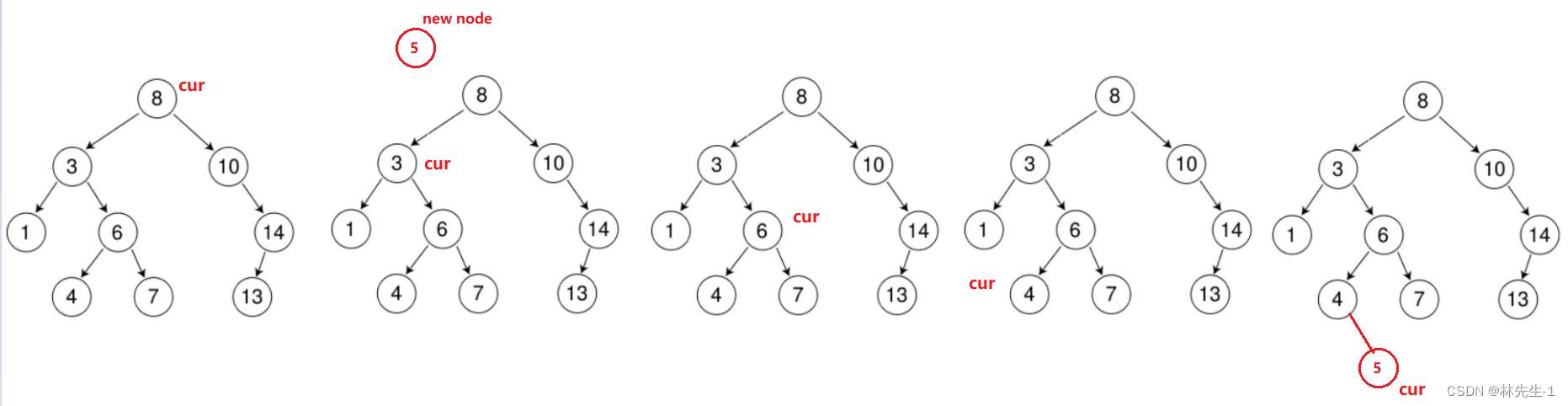
在这里插入图片描述
但是这样子，只是cur走到了空，我们并不是道cur是最有一个节点的做孩子还是右孩子，所以我们还需要一个parent指针一路记录cur的父亲，这样到cur走到空的时候就能判断是插入在左边还是右边了：
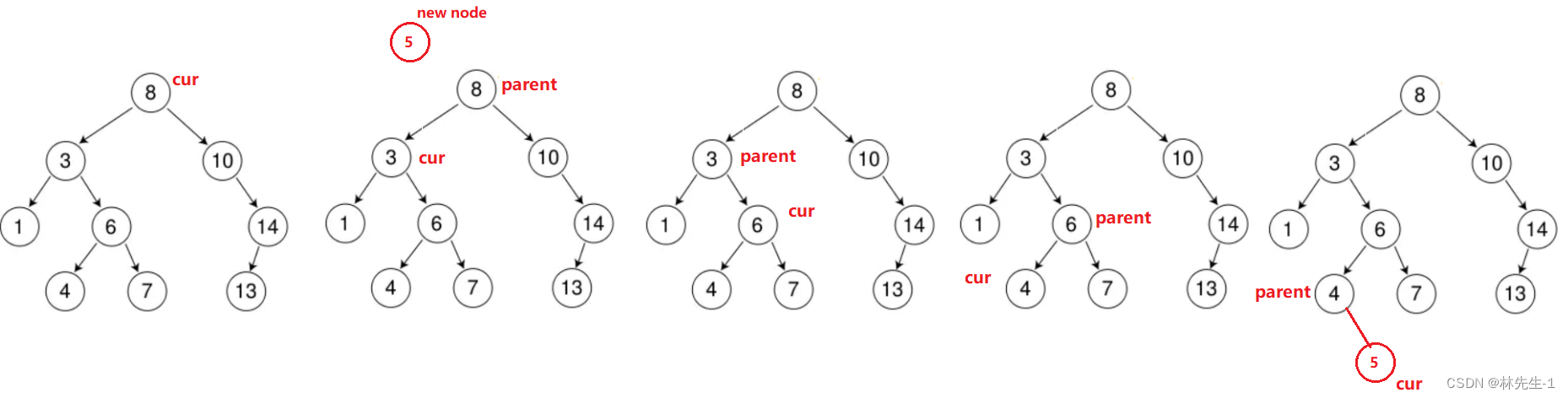
在这里插入图片描述

注意： 搜索二叉树是不能插入相同节点的。

代码实现：

// 非递归插入
	bool insert(const K& val) {
		if (nullptr == _root) {
			_root = new Node(val);
			return true;
		}
		Node* cur = _root;
		Node* parent = _root;
		while (cur) {
			parent = cur;
			if (val < cur->_val) {
				cur = cur->_left;
			}
			else if (val > cur->_val) {
				cur = cur->_right;
			}
			else { // 不能插入相同节点，如果相同直接返回false
				return false;
			}
		}
		// 判断插入在左还是在右
		if (val < parent->_val) {
			parent->_left = new Node(val);
		}
		else {
			parent->_right = new Node(val);
		}
		return true;
	}

2.1.2、查找

查找我想应该是最简单的了，我们按规矩走一遍就行了，如果找到就返回true，走到空就表示找不到，返回false即可：

// 非递归查找
bool Find(const K& val) {
	Node* cur = _root;
	while (cur) {
		if (val < cur->_val) {
			cur = cur->_left;
		}
		else if (val > cur->_val) {
			cur = cur->_right;
		}
		else {
			return true;
		}
	}
	return false;
}

2.1.3、删除

但删除就没有这么简单了，因为这得涉及到对这棵树局部的重新调整。
可能大家也能想到，删除叶子结点一定是最简单的，删除左右都不为空的节点一定是最难的。
但是叶子结点是左右都为空，我们其实可以将它分类到左为空或者右为空中，因为它两个条件都满足嘛。

左为空：
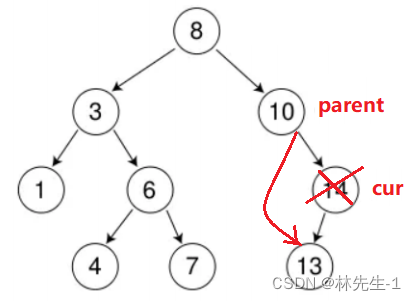
比如在下面这棵树中我们要删除10这个节点：
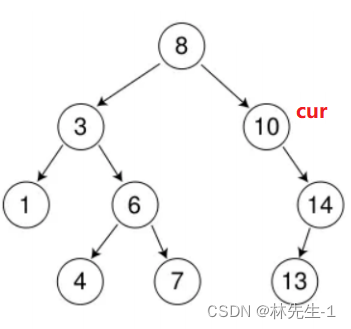
在这里插入图片描述
根据搜索二叉树的规则，我们会发现对于一个根节点，其左子树的所有节点都是小于它的，右子树的所有节点都是大于它的。
所以对于当前的情况，我们只需要将当前cur节点删除，然后让其父亲的左指针或右指针指向cur的右孩子即可：
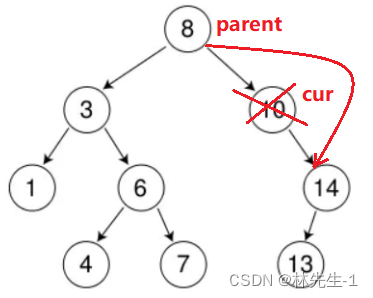
在这里插入图片描述
右为空：
同理，右为空的处理和左为空类似：
在这里插入图片描述

左右都不为空：
左右都不为空的情况就有点儿复杂了，因为这种情况cur牵扯到的节点一定是最多的，有可能cur的做右子树都是很大的树，可想要做的调整应该是很大的！？

但其实我们并需要做多大的调整，调整这种情况我们只需要把注意力放在搜索二叉树的“规则”上。

即对于每一棵子树，它的左孩子一定比它小，有孩子一定比它大。
而从这个规律中我们也能得到另个一规律，就是对于一个根而言，它的左子树的所有节点都一定比它小，它的右子树的所有节点都一定比它大。

我们从第二个规律入手就可以很好的解决了，那怎样做到调整之后保持这个规律呢？

先给出结论：

找出左/右字数中最大/小的节点，然后与cur交换，然后那个最小的节点(值已经交换，所以也就达到了删除cur的目的)。

以找到右子树的最小节点为例，我们来解释一下，这样做为什么行，比如在下面这棵树中，我们要上出节点3:
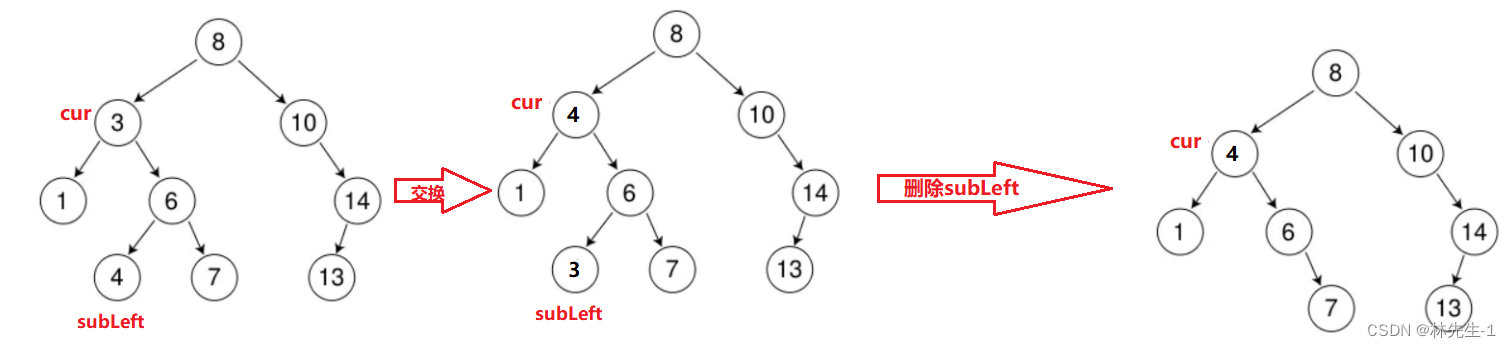
在这里插入图片描述
我们这里用subLeft来表示右子树的最小节点，cur表示当前要删除的节点。

由搜索二叉树的规律我们可知，一个树的最小节点一定是这棵树的最左节点，所以它一定是个叶子结点，所以删除subLeft就可以转化成和上面左/右为空的情况。
而一棵树的最小节点一定比这棵树中的所有节点都要小，又由上面的第二个结论，**我们可知subLeft一定是大于cur左子树中任意的节点的。**所以交换cur和subleft后的整棵子树依旧符合搜索二叉树的定义。

同理，选择右子树的最大节点也是同样的证明。

代码实现：

// 非递归删除
bool Erase(const K& val) {
	Node* cur = _root;
	Node* parent = _root;
	// 先找到要删除的节点
	while (cur) {
		if (val < cur->_val) {
			parent = cur;
			cur = cur->_left;
		}
		else if (val > cur->_val) {
			parent = cur;
			cur = cur->_right;
		}
		else {
			// 开始删除
			if (nullptr == cur->_left) { // 左为空
				if (cur == _root) { // 如果cur等于_root
					_root = _root->_right;
				}
				else {
					if (cur == parent->_left) {
						parent->_left = cur->_right;
					}
					else {
						parent->_right = cur->_right;
					}
				}
				delete cur;
			}
			else if (nullptr == cur->_right) { // 右为空
				if (cur == _root) {
					_root = _root->_left;
				}
				else {
					if (cur == parent->_left) {
						parent->_left = cur->_left;
					}
					else {
						parent->_right = cur->_left;
					}
				}
				delete cur;
			}
			else { // 左右都不为空
				Node* parent = cur;
				Node* subLeft = cur->_right; // 记录右子树中最小的节点
				// 找到右子树最小的节点(右子树中最左边的节点)
				while (subLeft->_left) {
					parent = subLeft;
					subLeft = subLeft->_left;
				}
				// 交换
				swap(subLeft->_val, cur->_val);
				// 转化成去删除subLeft
				if (subLeft == parent->_left) {
					parent->_left = subLeft->_right;
				}
				else {
					parent->_right = subLeft->_right;
				}
				delete subLeft;
			}
			return true;
		}
	}
	return false;
}

2.2、递归接口实现

我们以前的二叉树都是用递归实现的，二搜索二叉树也是二叉树，当然也可以使用递归实现。

2.2.1、插入

插入的递归实现其实很好写，如果要插入的节点比当前的节点小就转化成在左子树插入，如果要插入的节点把当前的节点大就转化成在右子树插入，如果相等就返回false即可。
用递归实现还有一个好处就是，我们没必要记录遍历到的每个节点的parent了，因为递归用传参的方式就很好的帮我们解决了。

先看代码实现：

// 递归版insert
bool insertR(const K& val) {
	return _insertR(_root, val); // 因为_root在类里面是私有的，在类外部不好传参，所以在这里设计了一个子函数
}
bool _insertR(Node *& root, const K & val) {
	if (nullptr == root) {
		root = new Node(val);
	}
	if (val < root->_val) {
		return _insertR(root->_left, val);
	}
	else if (val > root->_val) {
		return _insertR(root->_right, val);
	}
	return false;
}

不知道大家有没有注意到，我的_insertR子函数里的root指针给的是一个引用，为什么要给引用呢？如果不给引用的话会有什么问题呢？

先给出回答：这里的root必须给引用，如果不给引用的话新插入的节点和之前的节点就连接不上了。

为什么：
虽说现在已经是C++了，但是有时候解决一些问题还是需要用到C语言的知识的。
这里其实涉及到了C语言中变量的“左值”和“右值”的知识。

如下图：
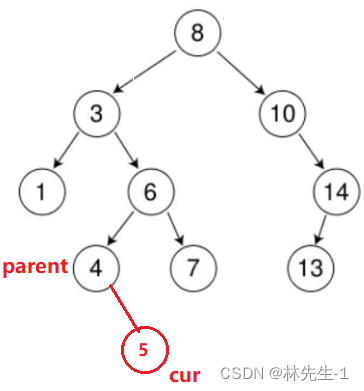
在这里插入图片描述
如果我们想要将新的节点连接上parent，要执行parent->_right = cur，这其实是将cur放到parent->_right指向的 “空间”，也就是要用到parent->_right的 “左值”(“左值”表示空间，“右值”表示数据)。

而如果我们不适用引用传参，则我们传过来的值是一个局部变量，是是实参的拷贝：
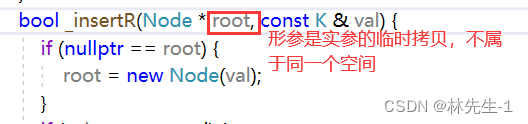
在这里插入图片描述
也就是说只传指针的话，我们只是将新节点放到了局部变量的空间中，所以就没有连接上。

如果想要连接成功，也可以像C语言一样使用二级指针，但是现在有C++的引用可以用，谁还用二级指针啊，二级指针多恶心啊！

所以我们这里就需要使用引用传参，引用是对象的别名，所以用的还是一样的左值，一样的空间。

2.2.2、查找

查找也是很简单的，几乎和循环一样。
如果要查找的节点比当前节点小，就递归到左子树查找，如果要查找的节点比当前节点大，就递归到右子树查找，如果递归到空节点，则说明找不到，返回false即可：

// 递归版查找
bool FindR(const K& val) {
	return _FindR(_root, val);
}
bool _FindR(Node* root, const K& val) {
	if (nullptr == root) {
		return false;
	}
	if (val < root->_val) {
		return _FindR(root->_left, val);
	}
	else if (val > root->_val) {
		return _FindR(root->_right, val);
	}
	return true;
}

2.2.3、删除

递归删除也是先要找到节点才行，这个不多说。
递归删除虽说是递归，但是我们只是借助递归帮我们查找节点而已，删除操作其实是和迭代的方式一样的，唯一不同的是，当删除到左右都不为空的节点时，我们交换后可以利用递归转化成在左子树或右子树中删除同样值：

// 递归版删除
bool EraseR(const K& val) {
	return _EraseR(_root, val);
}
bool _EraseR(Node*& root, const K& val) {
	if (root == nullptr) {
		return false;
	}
	if (val < root->_val) {
		return _EraseR(root->_left, val);
	}
	else if (val > root->_val) {
		return _EraseR(root->_right, val);
	}
	else {
		if (nullptr == root->_left) {
			// 开始删除(和迭代的方式一样)
			Node* del = root;
			root = root->_right;
			delete del;
			return true;
		}
		else if (nullptr == root->_right) {
			Node* del = root;
			root = root->_left;
			delete del;
			return true;
		}
		else {
			Node* subLeft = root->_right;
			// 找到右子树最小的节点(右子树中最左边的节点)
			while (subLeft->_left) {
				subLeft = subLeft->_left;
			}
			// 交换
			swap(subLeft->_val, root->_val);
		}
		// 转化成在右子树删除同样的值
		return _EraseR(root->_right, val);
	}
}

三、升级为K-V模型

我们上面所实现的其实可以称作是K模型的二叉搜索树，但二叉搜索树最多的应用其实是K-V模型。
K-V模型其实就是一个键对应一个值，比如英汉字典就是典型的K-V模型，中文是键，英文是值，在查找的时候只需要找到中文就可以得到对应的英文了。

搜索二叉树的K-V模型也是一样，在查找的时候我们只需要给出对应的key，就能找到对应的value。

想要将我们上面写的二叉搜索树改成K-V模型其实很简单，只需要多加一个模板参数，然后将对应的接口修改一下即可：

修改节点：

// 搜索二叉树节点
template <class K, class V>
struct BSTreeNode {
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;
	V _val;
	BSTreeNode(const K& keyl, const V& val)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
		,_val(val)
	{}
};

修改插入(非递归)：

// 非递归插入
bool insert(const K& key, const V& val) {
	if (nullptr == _root) {
		_root = new Node(key, val);
		return true;
	}
	Node* cur = _root;
	Node* parent = _root;
	while (cur) {
		parent = cur;
		if (keyl < cur->_key) {
			cur = cur->_left;
		}
		else if (key > cur->_key) {
			cur = cur->_right;
		}
		else {
			return false;
		}
	}
	if (key < parent->_key) {
		parent->_left = new Node(key, val);
	}
	else {
		parent->_right = new Node(key, val);
	}
	return true;
}

因为K-V模型只是通过key找到val，所以比较的时候置于key有关。

因为我们的插入和删除都是依照key来判断的，而删除并不涉及到修改，所以也就与val无关，所以删除的逻辑是一样的，不用修改。

修改查找：
因为我们这里改成了K-V模型，查找的话最好是能查找出一个键值对这样的效果更好，所以我们查找成功的话就直接返回节点的指针即可：

// 非递归查找
Node* Find(const K& keyl) {
	Node* cur = _root;
	while (cur) {
		if (keyl < cur->_key) {
			cur = cur->_left;
		}
		else if (keyl > cur->_key) {
			cur = cur->_right;
		}
		else {
			return cur;
		}
	}
	return nullptr;
}

修改完后我们可以浅浅的来测试一下，实现一个简易的单词查找功能：

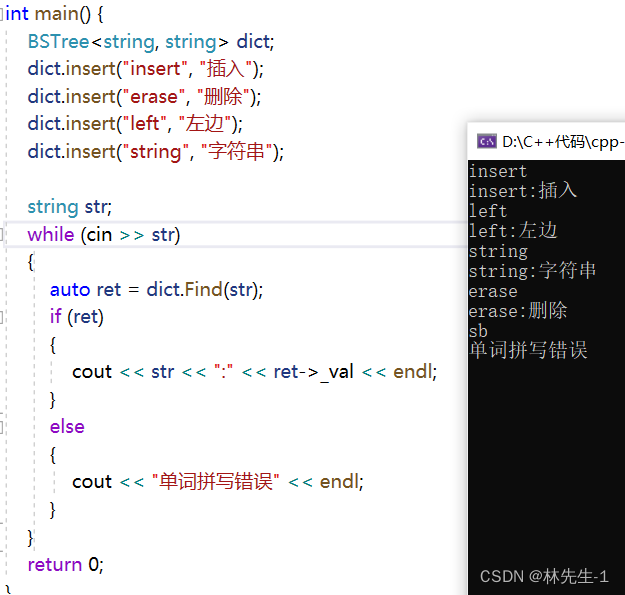
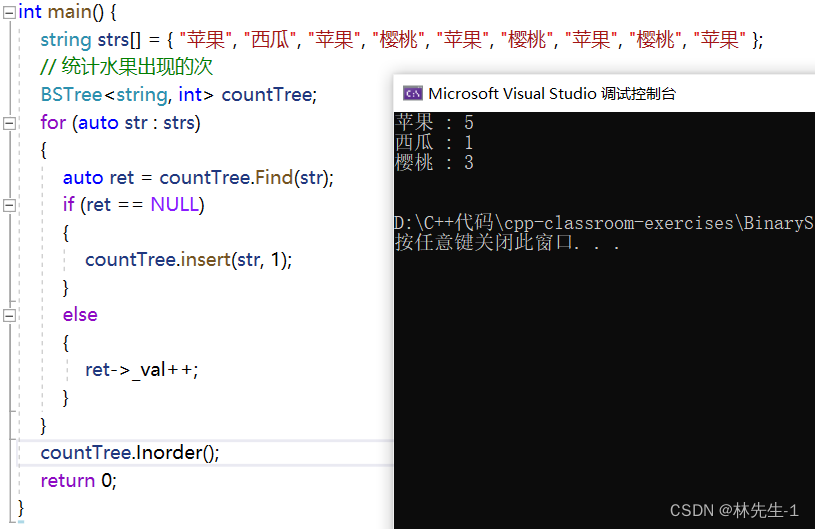
在这里插入图片描述

还有一个简易的统计频数的功能：
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1200113.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

grpc使用教程

grpc使用教程

准备 1&#xff0c;安装grpc go get -u google.golang.org/grpc2, 安装go语言protobuf生成器protoc-gen-go go get -u google.golang.org/protobuf/cmd/protoc-gen-go3, 通过下面连接&#xff0c;找到合适版本并安装protoc工具&#xff0c;如windows选择 protoc-3.19.5-win64.…
阅读更多...
c++类对象内存模型(一)

c++类对象内存模型(一)

C对象模型可以概括为以下2部分&#xff1a; 1. 语言中直接支持面向对象程序设计的部分&#xff0c;主要涉及如构造函数、析构函数、虚函数、继承&#xff08;单继承、多继承、虚继承&#xff09;、多态等等。 2. 对于各种支持的底层实现机制。在c语言中&#xff0c;“数据”和…
阅读更多...
时间序列预测实战(十四)Transformer模型实现长期预测并可视化结果（附代码+数据集+原理介绍）

时间序列预测实战(十四)Transformer模型实现长期预测并可视化结果（附代码+数据集+原理介绍）

论文地址->Transformer官方论文地址 官方代码地址->暂时还没有找到有官方的Transformer用于时间序列预测的代码地址 个人修改地址-> Transformer模型下载地址CSDN免费 一、本文介绍 这篇文章给大家带来是Transformer在时间序列预测上的应用&#xff0c;这种模型最…
阅读更多...
C++算法：包含三个字符串的最短字符串

C++算法：包含三个字符串的最短字符串

涉及知识点 有序集合 字符串 题目 给你三个字符串 a &#xff0c;b 和 c &#xff0c; 你的任务是找到长度 最短 的字符串&#xff0c;且这三个字符串都是它的 子字符串 。 如果有多个这样的字符串&#xff0c;请你返回 字典序最小 的一个。 请你返回满足题目要求的字符串。…
阅读更多...
2023年09月 Python（四级）真题解析#中国电子学会#全国青少年软件编程等级考试

2023年09月 Python（四级）真题解析#中国电子学会#全国青少年软件编程等级考试

Python等级考试（1~6级）全部真题・点这里 一、单选题（共25题，每题2分，共50分） 第1题 用枚举算法求解“100以内既能被3整除又能被4整除的元素”时，在下列数值范围内，算法执行效率最高的是？（　） A：1~101 B：4~100 C：12~100 D：12~96 答案：D 题目要求找出在 100…
阅读更多...
面向对象特征【继承性】

面向对象特征【继承性】

文章目录 基本概念继承的语法继承性的细节方法的重写方法重写的要求 基本概念 继承性允许子类继承父类的属性和方法。在Java中&#xff0c;使用关键字extends来实现继承。例如&#xff1a; class Animal {void eat() {System.out.println("动物正在吃");} }class D…
阅读更多...
绝了！现在制作电子期刊这么快而有效了？

绝了！现在制作电子期刊这么快而有效了？

​随着科技的进步&#xff0c;制作电子期刊已经变得越来越简单和高效。现在&#xff0c;您只需要一台电脑或手机&#xff0c;就可以快速制作出精美的电子期刊&#xff0c;而且还能有效地吸引读者的注意力。 但是如何快而有效的制作电子期刊呢&#xff1f; 1.首先打开FLBOOK在线…
阅读更多...
2023第六届泰迪杯数据分析

2023第六届泰迪杯数据分析

第六届带队”指导“请私信本人&#xff0c;团队包含技能赛双一等&#xff0c;数学建模省一&#xff0c;泰迪杯挖掘国一&#xff0c;研究生队友。 去年一等作品可视化图如下&#xff0c;私信获取源码
阅读更多...
[直播自学]-[汇川easy320]搞起来（4）看文档 查找设备(续）

[直播自学]-[汇川easy320]搞起来（4）看文档 查找设备(续）

2023.11.12 周六 19&#xff1a;05 补充一下关于以太网查找设备&#xff0c;如果设置如下&#xff1a; 然后点击测试&#xff1a; 点击ping&#xff1a;
阅读更多...
Windows下Oracle安装和卸载

Windows下Oracle安装和卸载

Windows下Oracle安装和卸载 1、Windows下安装Oracle 安装的版本&#xff1a;win32_11gR2_database。 解压之后双击setup.exe程序。 点击是。 配置安全更新&#xff0c;去掉复选框&#xff0c;点下一步。 提示未指定电子邮件地址&#xff0c;点是跳过。 配置安装选项&#xf…
阅读更多...
Java继承和多态（1）

Java继承和多态（1）

&#x1f435;本主题将分为篇文章&#xff0c;本篇文章将主要对继承进行讲解 一、介绍继承 1.1 什么是继承 假如有两个类&#xff1a;A类和B类&#xff0c;A类在保持原有成员变量和方法的基础上可以使用B类的成员变量和方法&#xff0c;此时就称A类继承了B类&#xff0c;A类为…
阅读更多...
4.1每日一题（多元函数微分：偏导数判定（链导法、定义、先代后求））

4.1每日一题（多元函数微分：偏导数判定（链导法、定义、先代后求））

链导法&#xff1a;如果每一层复合都可导&#xff08;即在判断点要可导&#xff09;&#xff0c;则复合函数一定可导&#xff1b;如果中间层有不可导&#xff0c;就不方便使用链导法了&#xff08;在&#xff08;0&#xff0c;0&#xff09;点不可导) 当链导法不好用时应该直接…
阅读更多...
微信支付平台C#SDK_微信支付.net SDK

微信支付平台C#SDK_微信支付.net SDK

一、微信支付平台C# SDK V3 https://github.com/fudiwei/DotNetCore.SKIT.FlurlHttpClient.Wechat/blob/main/docs/WechatTenpayV3 接口对应整理&#xff1a; https://github.com/fudiwei/DotNetCore.SKIT.FlurlHttpClient.Wechat/blob/main/docs/WechatTenpayV3/Basic_Mod…
阅读更多...
vue3响应式api

vue3响应式api

响应式api——compositon api setup&#xff1a; 不要再想this问题执行是在beforeCreated之前 beforeCreated&#xff1a;也就是创建了一个实例 created&#xff1a;挂载了数据 通过形参props接收&#xff0c;只读 以后所有代码都写到setup中 判断是否只读&#xff1a;isReadon…
阅读更多...
大数据可视化数据大屏可视化模板【可视化项目案例-05】

大数据可视化数据大屏可视化模板【可视化项目案例-05】

🎉🎊🎉 你的技术旅程将在这里启航！ 🚀🚀 本文选自专栏：可视化技术专栏100例 可视化技术专栏100例，包括但不限于大屏可视化、图表可视化等等。订阅专栏用户在文章底部可下载对应案例源码以供大家深入的学习研究。 🎓 每一个案例都会提供完整代码和详细的讲解，不…
阅读更多...
数据结构：AVLTree的插入和删除的实现

数据结构：AVLTree的插入和删除的实现

个人主页 &#xff1a; 个人主页 个人专栏 &#xff1a; 《数据结构》 《C语言》《C》 文章目录 前言一、AVLTree二、AVLTree的插入插入新增节点调整平衡因子旋转左单旋(新增节点位于较高右子树的右侧)右单旋(新增节点位于较高左子树的左侧)右左双旋(新增节点在较高右子树的左子…
阅读更多...
多数据源切换

多数据源切换

多数据源切换 1.jdbcTemplate2.使用切面3.mybatis层次的多数据源4.spring的dynamic自动注入 项目中经常会有多个数据源&#xff0c;那么如何处理呢 有4种方法 准备&#xff1a; 创建两个数据库 CREATE SCHEMA test DEFAULT CHARACTER SET utf8mb4 ; CREATE SCHEMA school DEFA…
阅读更多...
pandas笔记：读写excel

pandas笔记：读写excel

1 读excel read_excel函数能够读取的格式包含&#xff1a;xls, xlsx, xlsm, xlsb, odf, ods 和 odt 文件扩展名。 支持读取单一sheet或几个sheet。 1.0 使用的数据 1.1 主要使用方法 pandas.read_excel(io, sheet_name0, header0, namesNone, index_colNone, usecolsNon…
阅读更多...
Nginx：如何实现一个域名访问多个项目

Nginx：如何实现一个域名访问多个项目

1. 背景介绍 最近在多个项目部署中遇到这样一个问题&#xff0c;一个域名如何实现多个项目的访问。因为不想自己单独去申请域名证书和域名配置&#xff0c;便想到了这个方案&#xff0c;结合Nginx的location功能实现了自己的需求&#xff0c;便记录下来。示例中是以项目演示&a…
阅读更多...
基于Springboot菜谱美食饮食健康管理系统设计与实现

基于Springboot菜谱美食饮食健康管理系统设计与实现

博主介绍&#xff1a;✌Csdn特邀作者、博客专家、博客云专家、B站程序阿龙带小白做毕设系列&#xff0c;项目讲解、B站粉丝排行榜前列、专注于Java技术领域和毕业项目实战✌ 有设计项目或者是研究参考的可以加微信&#xff1a;Script-Liu 或者是QQ:1339941174 使用的软件开发环…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023