题目
给定一个正数n，求n的裂开方法数，
规定：后面的数不能比前面的数小
比如4的裂开方法有：
1+1+1+1、1+1+2、1+3、2+2、0+4 。 5种，所以返回5

暴力递归
用暴力递归方法进行尝试，整体思路是这样：

1. 暴力递归方法需要参数pre（上一个数拆分的大小是多少）和rest（剩余的数大小是多少）
2. 因为题目所说，base case也可以进行确定为
   2.1 pre > rest 则return 0 后面的数不能小于前面的数。
   2.2 如果拆分后的rest = 0，代表两种情况：
   第一种是满足pre < rest 的情况下全部拆完， return 1。
   另一种是我pre就是当前要拆分的数本身，此时也算是一种拆分方式，return 1。

代码

public static int ways(int n) {
        if (n < 0) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        return process(1, n);
    }

    public static int process(int pre, int rest) {
    	//两个if判断必须这个在前。
        if (rest == 0) {
            return 1;
        }
        if (pre > rest) {
            return 0;
        }
        int ways = 0;
        for (int first = pre; first <= rest; first++) {
            ways += process(first, rest - first);
        }
        return ways;
    }

动态规划
依然是根据暴力递归代码改写动态规划，首先根据可变参数pre、rest 确定dp[][]大小为dp[n + 1][n + 1]。
并且根据base case可以确定dp[0 ~ n][0]位置 = 1。并且dp[pre][pre]位置值也为1。
第一点比较好理解，第二个来解释一下。如下图所示：

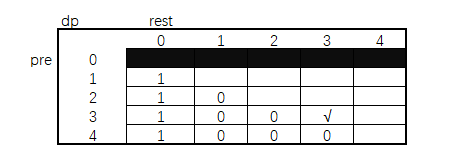
因为我暴力递归中ways主方法pre参数是从1开始尝试，所以pre = 0可以忽略不看。
根据base case rest = 0的列值为1，又因为pre 必须小于 rest ，所以 pre > rest的位置全都默认0，接下来我们来看 √ 位置 pre = 3 rest = 3。
这个位置可以将rest拆分成（1，2）、（2，1）、（3，0）。因为rest 要大于 pre。所以此时只有（3，0）这个选项可以进行拆分。拆分后，pre = 3， rest = 3，所以 √ 位置依赖pre = 3 rest = 0位置的数。
所以可以确定dp[pre][pre]对角线位置的值都为1。

代码

 public static int dp(int n) {
        if (n < 0) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        int[][] dp = new int[n + 1][n + 1];

        for (int pre = 1; pre <= n; pre++) {
            dp[pre][0] = 1;
            dp[pre][pre] = 1;
        }

        for (int pre = n - 1; pre >= 1; pre--) {
            for (int rest = pre + 1; rest <= n; rest++) {
                int ways = 0;
                for (int first = pre; first <= rest; first++) {
                    ways += dp[first][rest - first] ;
                }
                dp[pre][rest] = ways;
            }
        }
        return dp[1][n];
    }

再次优化
可以看到动态规划的代码中依然还有枚举过程可以进行优化，我们仍然是画图，看每个dp格子之间的位置依赖。如下图所示：
此时我在（2，4）位置，接下来再次进行拆分，会看到它依赖的格子有（2，2）、（3，1）、（4，0）。

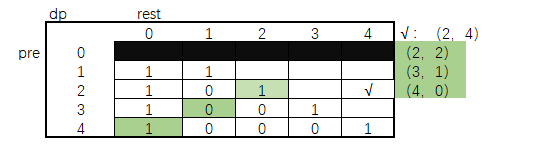
再看x位置（3，4）,继续拆分依赖的是（3，1）、（4，0）位置。

如果将它抽象化的话，此时的pre rest依赖的就是 pre, rest -pre。和 pre + 1，rest的位置。就可以用这个公式将枚举行为来替换掉。

代码

 public static int bestDP(int n) {
        if (n < 0) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        int[][] dp = new int[n + 1][n + 1];

        for (int pre = 1; pre <= n; pre++) {
            dp[pre][0] = 1;
            dp[pre][pre] = 1;
        }

        for (int pre = n - 1; pre >= 1; pre--) {
            for (int rest = pre + 1; rest <= n; rest++) {
                dp[pre][rest] = dp[pre + 1][rest] + dp[pre][rest - pre];
            }
        }
        return dp[1][n];
    }