---

一.题目描述

求一个 3 X 3 的整型矩阵对角线元素之和

---

二.代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int main()
{
	int arr[3][3] = { 0 };
	for (int i = 0;i < 3;i++)
	{
		for (int j = 0;j < 3;j++)
		{	
			printf("请输入数字：");
			scanf("%d", &arr[i][j]);
		}
	}
	printf("和为%d", arr[0][0] + arr[1][1] + arr[2][2]);
	return 0;
}

---

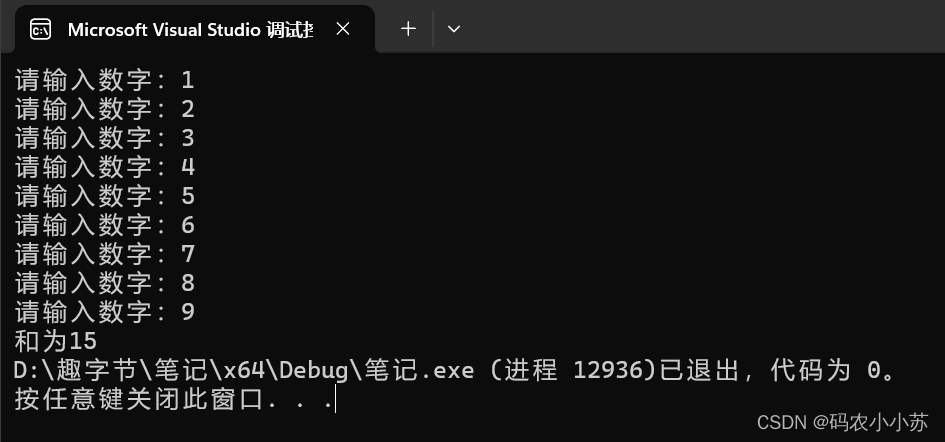
 三.运行结果

---

创作不易， 如果这份博客👍对你有帮助，可以给博主一个免费的点赞以示鼓励。
欢迎各位帅哥美女点赞👍评论⭐收藏⭐，谢谢！！！
如果有什么疑问或不同的见解，欢迎在评论区留言哦👀。
祝各位生活愉快⭐