[C++随想录] map和set的封装

news2025/1/9 17:16:08

map和set的封装

  • 1. 红黑树模版的改变
    • 1.1 RBTree类模板 头的改变
    • 1.2 封装迭代器类
      • 1.2.1 构造 && 拷贝构造
      • 1.2.2. ++
      • 1.2.3. - -
      • 1.2.4. 其他运算符重载
    • 1.3 RBTree类实现普通迭代器和const迭代器
  • 2. set的底层逻辑
  • 3. map的底层逻辑
  • 4. 源码
    • 4.1 RBTree类
    • 4.2 set类
    • 4.3 map类

1. 红黑树模版的改变

1.1 RBTree类模板 头的改变

原来的红黑树模版是 <class K, class V>
由于 set 的存储数据是K类型, 而map的存储数据是 <K, V>类型
⇒ 红黑树的模版要进行改变


🗨️ set中控制 key不允许修改为什么不用 RBTree<K, const K, SetofT>?

  • 见set中 普通迭代器 和 const迭代器的实现

1.2 封装迭代器类

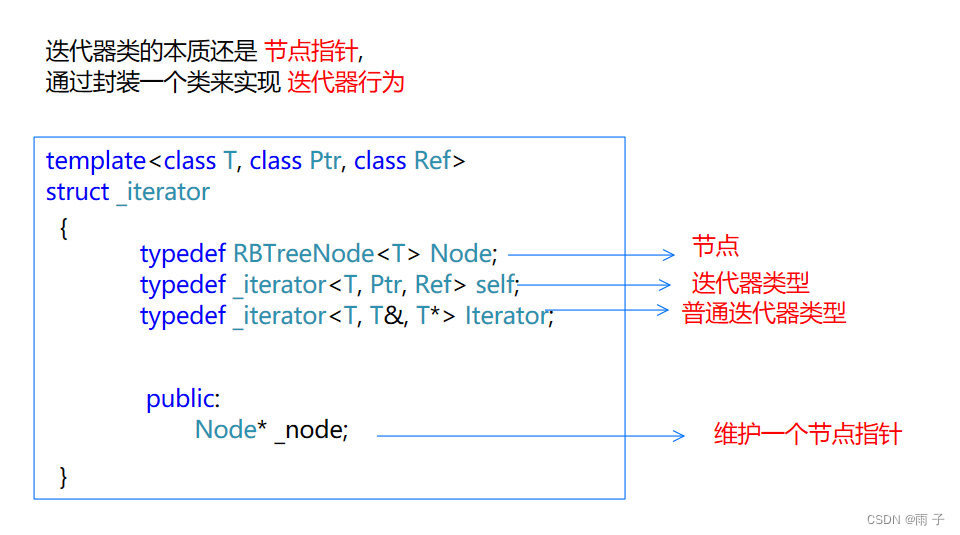
1.2.1 构造 && 拷贝构造

  1. 构造
_iterator(Node* t)
	:_node(t)
{}
  1. 用普通迭代器初始化const迭代器
// 用普通迭代器去初始化const迭代器
_iterator(const Iterator& it)
	:_node(it._node)
{}

🗨️为什么要写 用普通迭代器初始化const迭代器呢 ?

  • 见set的 insert逻辑
    按照道理来说, 迭代器是 内置类型 ⇒ 浅拷贝, 是不需要我们亲自写拷贝构造的

1.2.2. ++

++ — — 返回 中序 中的下一个节点
由于 中序是 左跟右 ⇒ 当前节点 ++ 主要有两大情况 右子树为空, 右子树不为空

  1. 右子树为空, 说明当前根节点的右子树的逻辑并没有结束, 意味着要找到右子树的最小节点
  2. 右子树为空, 说明当前根节点的整个逻辑已经结束(左子树向上, 向根节点返回左子树的情况), 意味着要找到最近的孩子是父亲左孩子的父亲节点
self& operator++()
{
	// 右子树不为空
	if (_node->_right)
	{
		Node* rightmin = _node->_right;
		while (rightmin->_left)
		{
			rightmin = rightmin->_left;
		}
		_node = rightmin;
	}
	// 右子树为空
	// 向上回溯并返回最近的孩子是父亲左孩子的父亲节点
	else
	{
		Node* cur = _node;
		Node* parent = cur->_parent;
		while (parent && cur == parent->_right)
		{
			cur = parent;
			parent = parent->_parent;
		}
		_node = parent;
	}

	return *this;
}

1.2.3. - -

减减 — — 加加反过来, 右跟左
当前节点减减, 主要有两大情况 左子树为空, 左子树不问空

  1. 左子树不为空, 说明当前根结点的左子树逻辑并没有结束, 意味着要找到左子树中的最大节点
  2. 左子树为空, 说明当前根节点的这个逻辑已经结束(右子树向上, 向根节点返回右子树的情况), 意味着要找到最近的 孩子是父亲右孩子的父亲节点
self& operator--()
{
	// 左子树不为空
	if (_node->_left)
	{
		Node* leftmost = _node->_left;
		while (leftmost->_right)
		{
			leftmost = leftmost->_right;
		}
		_node = leftmost;
	}
	// 左子树为空
	// 找到最近的孩子是父亲右孩子的父亲节点
	else
	{
		Node* cur = _node;
		Node* parent = cur->_parent;
		while (parent && parent->_left == cur)
		{
			cur = parent;
			parent = parent->_parent;
		}
		_node = parent;
	}

	return *this;
}

1.2.4. 其他运算符重载

  1. operator!=
bool operator !=(const self& t)
{
	return _node != t._node;
}
  1. operator==
bool operator ==(const self& t)
{
	return _node->_data == t._node;
}
  1. operator*
Ptr operator*()
{
	return _node->_data;
}
  1. operator->
Ref operator->()
{
	return &_node->_data;
}

1.3 RBTree类实现普通迭代器和const迭代器

  1. 类型
typedef _iterator<T, T&, T*> iterator;
typedef _iterator<T, const T&, const T*> const_iterator;
  1. begin, end
// begin - 最左节点
iterator begin()
{
	Node* leftmin = _root;
	while (leftmin && leftmin->_left)
	{
		leftmin = leftmin->_left;
	}
	
	// return iterator(leftmin);
	return leftmin;
}

iterator end()
{
	return iterator(nullptr);
}

const_iterator begin()const
{
	Node* leftmin = _root;
	while (leftmin && leftmin->_left)
	{
		leftmin = leftmin->_left;
	}
	
	// return const_iterator(leftmin);
	return leftmin;
}

const_iterator end()const
{
	return const_iterator(nullptr);
}

2. set的底层逻辑

  1. SetofT
  • 底层RBTree类中, 只知道数据类型是 T, 而不知道 set 和 map的具体数据类型 && set的数据类型是 K, 而map的数据类型是pair<K, V>⇒ 这个模版T实现了 泛型编程
    但是有一点是相同的, 都需要 数据中的 key 来进行比较逻辑 ⇒ 我们需要一个函数来 提取数据中的key

set中数据类型是K, key的类型也是 K ⇒ 我们 直接返回

struct SetofT
{
	const K& operator()(const K& data)
	{
		return data;
	}
};
  1. 迭代器
typedef typename RBTree<K, K, SetofT>::const_iterator iterator;
typedef typename RBTree<K, K, SetofT>::const_iterator const_iterator;

我们发现 : set中 迭代器 和 const迭代器都是 const迭代器 ⇒ 保证了 key是不能进行修改的
🗨️ set中控制 key不允许修改为什么不用 RBTree<K, const K, SetofT>?

  • 如果数据类型直接传 const类型 ⇒ 常量 ⇒ 常量, 结构是不成立的
  1. begin, end
    一个const版本即可
iterator begin()const
{
	return _t.begin();
}

iterator end()const
{
	return _t.end();
}
  1. find
iterator find(const K& key)
{
	return _t.find(key);
}
  1. insert
pair<iterator, bool>& insert(const K& data)
{
	pair<RBTree<K, K, SetofT>::iterator, bool> tem = _t.Insert(data);
	pair<iterator, bool> res = tem;
	return res;
}
  • 返回值是 pair结构的原因:
    map的 [ ] 的本质是调用 insert, 有如下功能: (以 map[ret] 为例子)
    1. ret 在map中存在, 返回value
    2. ret 在map中不存在, 则新插入该节点

⇒ 这就要求insert 返回的是一个 pair结构, <节点迭代器, 是否存在> ⇒ pair<iterator, bool>
由于 set 和 map 共用同一个 红黑树 ⇒ set中的 insert的返回值也是一个 pair结构

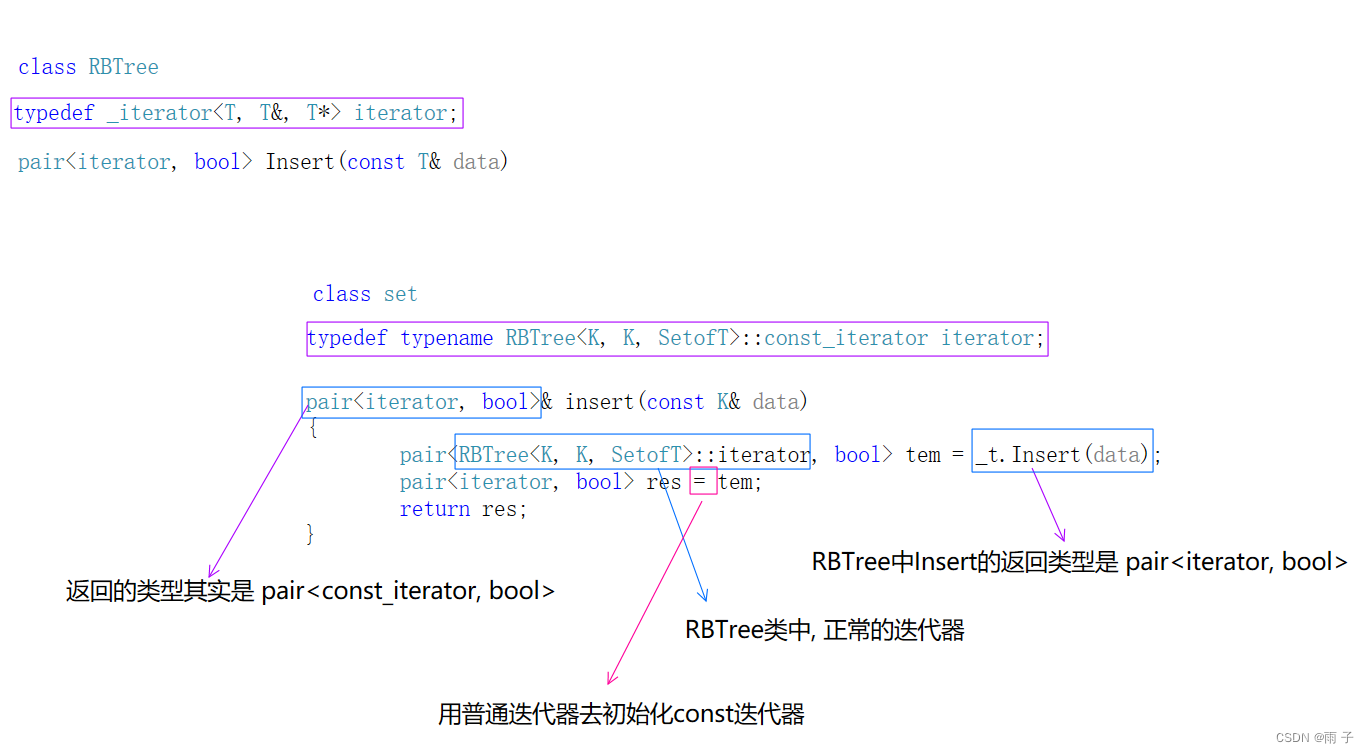
  • 进行类型转换的原因
    注意: set中的iterator是 const_iterat
    而RBTree中 Insert的返回值是 pair<iterator, bool> && RBTre类中的 iterator是正常的, 是普通迭代器
    ⇒ 就会出现 pair<const_iterator, bool> = pair<iterator, bool> 的类型不匹配问题
    由于 普通迭代器是可以初始化const迭代器的 (在RBTree类中的 迭代器类中要多一个 用普通迭代器去初始化const迭代器的函数 ) ⇒ 所以, 我们要先接收一下 Insert的返回值, 然后再进行类型转换

3. map的底层逻辑

  1. MapofT
struct MapofT
{
	const K& operator()(const pair<K, V>& data)
	{
		return data.first;
	}
};
  1. 迭代器
typedef typename RBTree<K, pair<const K, V>, MapofT>::iterator iterator;
typedef typename RBTree<K, pair<const K, V>, MapofT>::const_iterator const_iterator;
  1. begin, end
iterator begin()
{
	return _t.begin();
}

iterator end()
{
	return _t.end();
}

const_iterator begin()const
{
	return _t.begin();
}

const_iterator end()const
{
	return _t.end();
}
  1. find
iterator find(const K& key)
{
	return _t.find(key);
}
  1. insert
pair<iterator, bool> insert(const pair<K, V>& data)
{
	return _t.Insert(data);
}
  1. operator[ ]
V& operator[](const K& key)
{
	pair<iterator, bool> ret = insert(make_pair(key, V()));
	return ret.first->second;
}

4. 源码

4.1 RBTree类

#pragma once

#include<iostream>
#include<assert.h>

using namespace std;

	// 枚举
	enum Color
	{
		RED,
		BLACK 
	};

	template<class T>
	struct RBTreeNode
	{
	public:
		RBTreeNode(const T& data)
			:_data(data)
		{}

	public:
		T _data;
		Color _color = BLACK;
		RBTreeNode<T>* _left = nullptr;
		RBTreeNode<T>* _right = nullptr;
		RBTreeNode<T>* _parent = nullptr;
	};

	template<class T, class Ptr, class Ref>
	struct _iterator
	{
		typedef RBTreeNode<T> Node;
		typedef _iterator<T, Ptr, Ref> self;
		typedef _iterator<T, T&, T*> Iterator;

	public:

		// 用普通迭代器去初始化const迭代器
		_iterator(const Iterator& it)
			:_node(it._node)
		{}

		_iterator(Node* t)
			:_node(t)
		{}

		bool operator !=(const self& t)
		{
			return _node != t._node;
		}
		bool operator ==(const self& t)
		{
			return _node->_data == t._node;
		}

		Ptr operator*()
		{
			return _node->_data;
		}

		Ref operator->()
		{
			return &_node->_data;
		}

		self& operator++()
		{
			if (_node->_right)
			{
				Node* rightmin = _node->_right;
				while (rightmin->_left)
				{
					rightmin = rightmin->_left;
				}
				_node = rightmin;
			}
			else
			{
				Node* cur = _node;
				Node* parent = cur->_parent;
				while (parent && cur == parent->_right)
				{
					cur = parent;
					parent = parent->_parent;
				}
				_node = parent;
			}

			return *this;
		}

		self& operator--()
		{
			if (_node->_left)
			{
				Node* leftmost = _node->_left;
				while (leftmost->_right)
				{
					leftmost = leftmost->_right;
				}
				_node = leftmost;
			}
			else
			{
				Node* cur = _node;
				Node* parent = cur->_parent;
				while (parent && parent->_left == cur)
				{
					cur = parent;
					parent = parent->_parent;
				}
				_node = parent;
			}

			return *this;
		}

	public:
		Node* _node;

	};

	template<class K, class T, class KeyofT>
	struct RBTree
	{
		typedef RBTreeNode<T> Node;
	public:

		typedef _iterator<T, T&, T*> iterator;
		typedef _iterator<T, const T&, const T*> const_iterator;

	public:

		iterator begin()
		{
			Node* leftmin = _root;
			while (leftmin && leftmin->_left)
			{
				leftmin = leftmin->_left;
			}

			return leftmin;
		}

		iterator end()
		{
			return iterator(nullptr);
		}

		const_iterator begin()const
		{
			Node* leftmin = _root;
			while (leftmin && leftmin->_left)
			{
				leftmin = leftmin->_left;
			}

			return leftmin;
		}

		const_iterator end()const
		{
			return const_iterator(nullptr);
		}

		Node* find(const K& key)
		{
			KeyofT kot;

			Node* cur = _root;
			while (cur)
			{
				if (key > kot(cur->_data))
				{
					cur = cur->_right;
				}
				else if (key < kot(cur->_data))
				{
					cur = cur->_left;
				}
				else
				{
					return cur;
				}
			}

			return nullptr;
		}

		void RotateL(Node* parent)
		{
			++RotateCount;

			Node* cur = parent->_right;
			Node* grandfather = parent->_parent;
			Node* curleft = cur->_left;

			// 旋转核心
			parent->_right = curleft;
			cur->_left = parent;

			// 更新父亲
			// 1. parent && curleft
			if (curleft)
			{
				curleft->_parent = parent;
			}
			parent->_parent = cur;

			// 2.更新cur
			if (grandfather == nullptr)
			{
				cur->_parent = nullptr;
				_root = cur;
			}
			else
			{
				if (grandfather->_left == parent)
				{
					grandfather->_left = cur;
				}
				else
				{
					grandfather->_right = cur;
				}

				cur->_parent = grandfather;
			}

		}

		void RotateR(Node* parent)
		{
			++RotateCount;

			Node* cur = parent->_left;
			Node* grandfather = parent->_parent;
			Node* curright = cur->_right;

			// 旋转核心
			parent->_left = curright;
			cur->_right = parent;

			// 更新链接关系
			// 1. parent && curright
			if (curright)
			{
				curright->_parent = parent;
			}
			parent->_parent = cur;

			// 2.更新cur
			if (grandfather == nullptr)
			{
				cur->_parent = nullptr;
				_root = cur;
			}
			else
			{
				if (grandfather->_left == parent)
				{
					grandfather->_left = cur;
				}
				else
				{
					grandfather->_right = cur;
				}

				cur->_parent = grandfather;
			}
		}

		pair<iterator, bool> Insert(const T& data)
		{
			KeyofT kot;
			if (_root == nullptr)
			{
				// 根节点是黑色的
				_root = new Node(data);
				_root->_color = BLACK;
				return make_pair(iterator(_root), true);
			}

			Node* parent = _root;
			Node* cur = _root;
			while (cur)
			{
				if (kot(data) > kot(cur->_data))
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (kot(data) < kot(cur->_data))
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return make_pair(iterator(cur), false);
				}
			}

			// 新建一个节点, 默认是红色
			cur = new Node(data);
			cur->_color = RED;

			// 链接cur 和 parent
			if (kot(cur->_data) > kot(parent->_data))
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}
			cur->_parent = parent;

			// 更改黑红比例
			while (parent && parent->_color == RED)
			{
				Node* grandfather = parent->_parent;

				if (grandfather->_left == parent)
				{
					Node* uncle = grandfather->_right;

					// u存在且为红
					if (uncle && uncle->_color == RED)
					{
						// 颜色变化
						grandfather->_color = RED;
						parent->_color = uncle->_color = BLACK;

						// 继续向上调整
						cur = grandfather;
						parent = cur->_parent;
					}
					else // u不存在 或 u存在且为黑色
					{
						if (cur == parent->_left)
						{
							RotateR(grandfather);

							grandfather->_color = RED;
							parent->_color = BLACK;
						}
						else
						{
							RotateL(parent);
							RotateR(grandfather);

							cur->_color = BLACK;
							grandfather->_color = RED;
						}

						break;
					}
				}
				else if (grandfather->_right == parent)
				{
					Node* uncle = grandfather->_left;

					// u存在且为红
					if (uncle && uncle->_color == RED)
					{
						// 颜色变化
						grandfather->_color = RED;
						uncle->_color = parent->_color = BLACK;

						// 继续向上调整
						cur = grandfather;
						parent = cur->_parent;
					}
					// u不存在 或 u存在且为黑色
					else
					{
						if (parent->_right == cur)
						{
							RotateL(grandfather);

							parent->_color = BLACK;
							grandfather->_color = RED;
						}
						else
						{
							RotateR(parent);
							RotateL(grandfather);

							cur->_color = BLACK;
							grandfather->_color = RED;
						}

						break;
					}
				}
				else
				{
					assert("黑红比例失控!");
				}
			}

			// 暴力统一处理根节点的颜色
			_root->_color = BLACK;

			return make_pair(iterator(cur), true);
		}

		int Height()
		{
			return Height(_root);
		}

		int Height(Node* root)
		{
			if (root == nullptr)
				return 0;

			int left = Height(root->_left);
			int right = Height(root->_right);

			return left > right ? left + 1 : right + 1;
		}

		bool CheckColour(Node* root, int blacknum, int benchmark)
		{
			if (root == nullptr)
			{
				if (blacknum != benchmark)
					return false;

				return true;
			}

			if (root->_color == BLACK)
			{
				++blacknum;
			}

			if (root->_color == RED && root->_parent && root->_parent->_color == RED)
			{
				cout << root->_kv.first << "出现连续红色节点" << endl;
				return false;
			}

			return CheckColour(root->_left, blacknum, benchmark)
				&& CheckColour(root->_right, blacknum, benchmark);
		}

		bool IsBalance()
		{
			return IsBalance(_root);
		}

		bool IsBalance(Node* root)
		{
			if (root == nullptr)
				return true;

			if (root->_color != BLACK)
			{
				return false;
			}

			// 基准值
			int benchmark = 0;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_color == BLACK)
					++benchmark;

				cur = cur->_left;
			}

			return CheckColour(root, 0, benchmark);
		}

		int GetRoateCount()
		{
			return RotateCount;
		}

	private:
		Node* _root = nullptr;
		int RotateCount = 0;
	};

4.2 set类

#pragma once

#include"RBTree.h"

namespace muyu
{

	template<class K>
	class set
	{
		struct SetofT
		{
			const K& operator()(const K& data)
			{
				return data;
			}
		};

	public:
		typedef typename RBTree<K, K, SetofT>::const_iterator iterator;
		typedef typename RBTree<K, K, SetofT>::const_iterator const_iterator;


	public:
		pair<iterator, bool>& insert(const K& data)
		{
			pair<RBTree<K, K, SetofT>::iterator, bool> tem = _t.Insert(data);
			pair<iterator, bool> res = tem;
			return res;
		}

		iterator begin()const
		{
			return _t.begin();
		}

		iterator end()const
		{
			return _t.end();
		}

		iterator find(const K& key)
		{
			return _t.find(key);
		}

	private:
		RBTree<K, K, SetofT> _t;
	};
}

4.3 map类

#pragma once

#include"RBTree.h"

namespace muyu
{

	template<class K, class V>
	class map
	{
		struct MapofT
		{
			const K& operator()(const pair<K, V>& data)
			{
				return data.first;
			}
		};
	public:
		typedef typename RBTree<K, pair<const K, V>, MapofT>::iterator iterator;
		typedef typename RBTree<K, pair<const K, V>, MapofT>::const_iterator const_iterator;


	public:
		pair<iterator, bool> insert(const pair<K, V>& data)
		{
			return _t.Insert(data);
		}

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		const_iterator begin()const
		{
			return _t.begin();
		}
		
		iterator find(const K& key)
		{
			return _t.find(key);
		}
		
		const_iterator end()const
		{
			return _t.end();
		}

		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = insert(make_pair(key, V()));
			return ret.first->second;
		}

	private:
		RBTree<K, pair<const K, V>, MapofT> _t;
	};
}

遥望中原，荒烟外、许多城郭。
想当年、花遮柳护，凤楼龙阁。
万岁山前珠翠绕，蓬壶殿里笙歌作。
到而今、铁骑满郊畿，风尘恶。
兵安在？膏锋锷。
民安在？填沟壑。
叹江山如故，千村寥落。
何日请缨提锐旅，一鞭直渡清河洛。
却归来、再续汉阳游，骑黄鹤。
— — 岳飞《满江红·登黄鹤楼有感》

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1199190.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

20分钟搭建Ubertooth One开源蓝牙测试工具

20分钟搭建Ubertooth One开源蓝牙测试工具

kali linux 2023 安装依赖&#xff08;记得使用root用户搭建环境&#xff09; 1、apt-get update 2、apt install ubertooth 更新共享库缓存 3、ldconfig 安装 Ubertooth 工具和驱动程序 4、插入Ubertooth One工具 5、ubertooth-util -v 备注&#xff1a;出现Firmwate v…
阅读更多...
mac homebrew.mxcl.php@5.6.plist

mac homebrew.mxcl.php@5.6.plist

今天启动php5.6时 遇到了一个问题 servers % brew services start php5.6 Bootstrap failed: 5: Input/output error Try re-running the command as root for richer errors. Error: Failure while executing; /bin/launchctl bootstrap gui/501 /Users/ssh/Library/LaunchAge…
阅读更多...
【龙芯固件】ACPI——简介

【龙芯固件】ACPI——简介

一、 什么是ACPI ACPI是Hewlett-Packard, Intel, Microsoft, Phoenix, 和Toshiba共同制定的一个开放的行业规范。 ACPI由很多表组成&#xff0c;包括&#xff1a;RSDP&#xff0c;SDTH&#xff0c;RSDT&#xff0c;FADT&#xff0c;FACS&#xff0c;DSDT&#xff0c;SSDT&…
阅读更多...
C51--PC通过串口（中断）点亮LED

C51--PC通过串口（中断）点亮LED

B4中的&#xff1a;REN允许 / 禁止串行接收控制位 REN 1为允许串行接收状态。 接收数据必须开启。所以SCON&#xff1a;0101 0000 &#xff1b;即0x50 如何知道数据已经接收 RI位&#xff1a;当收到数据后 RI 1&#xff08;由硬件置一&#xff09; 硬件置一后必须用软件…
阅读更多...
Java 面试题之 Logback 打印日志是如何获取当前方法名称的？

Java 面试题之 Logback 打印日志是如何获取当前方法名称的？

在 Java 中&#xff0c;有四种方法可以获取当前正在执行方法体的方法名称&#xff0c;分别是&#xff1a; 使用 Thread.currentThread().getStackTrace() 方法 使用异常对象的 getStackTrace() 方法 使用匿名内部类的 getClass().getEnclosingMethod() 方法 Java 9 的 Stack…
阅读更多...
新生儿夜惊：原因、科普和注意事项

新生儿夜惊：原因、科普和注意事项

引言&#xff1a; 新生儿夜惊是一种常见的现象&#xff0c;它可能让新父母感到焦虑和不安。夜惊通常表现为婴儿在夜间忽然惊醒、哭闹&#xff0c;并伴随着呼吸急促和肌肉紧张。尽管这在大多数情况下是正常的生理现象&#xff0c;但对于父母来说&#xff0c;了解夜惊的原因和适…
阅读更多...
单链表指定结点的后插 前插操作

单链表指定结点的后插 前插操作

指定结点的后插操作 #define NULL 0typedef struct LNode {int data;struct LNode* next; }LNode, * LinkList;//后插操作&#xff1a;在p结点后插入元素e bool InsertNextNode(LNode* p, int e) {if (p NULL)return false;LNode* s (LNode*)malloc(sizeof(LNode));if (s N…
阅读更多...
（一）正点原子I.MX6ULL kernel6.1移植

（一）正点原子I.MX6ULL kernel6.1移植

一、概述 学完了正点原子的I.MX6ULL移植&#xff0c;正点原子的教程是基于Ubuntu18&#xff0c;使用的是4.1.15的内核&#xff0c;很多年前的了。NXP官方也发布了新的6.1的内核&#xff0c;以及2022.04的uboot。 本文分享一下基于Ubuntu22.04&#xff08;6.2.0-36-generic&…
阅读更多...
[LeetCode周赛复盘] 第 371 场周赛20231112

[LeetCode周赛复盘] 第 371 场周赛20231112

[LeetCode周赛复盘] 第 371 场周赛20231112 一、本周周赛总结100120. 找出强数对的最大异或值 I1. 题目描述2. 思路分析3. 代码实现 100128. 高访问员工1. 题目描述2. 思路分析3. 代码实现 100117. 最大化数组末位元素的最少操作次数1. 题目描述2. 思路分析3. 代码实现 100124…
阅读更多...
Flink SQL 表值聚合函数（Table Aggregate Function）详解

Flink SQL 表值聚合函数（Table Aggregate Function）详解

使用场景&#xff1a; 表值聚合函数即 UDTAF&#xff0c;这个函数⽬前只能在 Table API 中使⽤&#xff0c;不能在 SQL API 中使⽤。 函数功能&#xff1a; 在 SQL 表达式中&#xff0c;如果想对数据先分组再进⾏聚合取值&#xff1a; select max(xxx) from source_table gr…
阅读更多...
非遗文化展示预约小程序的效果如何

非遗文化展示预约小程序的效果如何

漫漫历史长河&#xff0c;我国积累的各种非遗文化广而多&#xff0c;也有相应的机构整理展示和收录&#xff0c;区域限制下&#xff0c;传统非遗文化内容传播度并不高&#xff0c;实际线下查看了解的人也并不是很多&#xff0c;在实际展示方面也面临着一些难题&#xff1a; 线…
阅读更多...
CS224W6.1——介绍图神经网络GNN

CS224W6.1——介绍图神经网络GNN

之前我们讨论了一些节点嵌入技术&#xff0c;它们可以通过随机游走的过程学习与任务无关的特征。从这篇开始&#xff0c;我们介绍了令人兴奋的图神经网络技术&#xff0c;该技术基于图结构用多层非线性变换对节点特征进行编码。图神经网络在各种任务中表现出非凡的性能&#xf…
阅读更多...
【数据库开发】DataX开发环境的安装部署

【数据库开发】DataX开发环境的安装部署

文章目录 1、简介1.1 DataX简介1.2 DataX功能1.3 支持的数据通道 2、DataX安装配置2.1 DataX2.2 Java2.3 Python2.4 测试 3、DataX Web安装配置3.1 mysql3.2 DataX Web3.2.1 简介3.2.2 架构图3.2.3 依赖环境3.2.4 安装 结语 1、简介 DataX是阿里云DataWorks数据集成的开源版本。…
阅读更多...
安装纯净版Linux后的必备设置

安装纯净版Linux后的必备设置

目录 一&#xff1a;网络设置 1&#xff0c;设置yum源 2&#xff0c;配置网络 二&#xff1a;samba服务设置 1&#xff0c;安装samba 2&#xff0c;设置samba 3&#xff0c;windows上挂载 三&#xff1a;安装必备的开发软件 1&#xff0c;GCC安装 2&#xff0c;Pyth…
阅读更多...
阿里云OSS和腾讯云COS对象存储介绍和简单使用

阿里云OSS和腾讯云COS对象存储介绍和简单使用

对象存储指的是一种云存储服务&#xff0c;其主要是将数据以对象的形式存储在云端&#xff0c;并且提供了完全的API调用&#xff0c;这些API包括上传&#xff0c;下载&#xff0c;删除&#xff0c;复制&#xff0c;预览&#xff0c;权限设置等等。OSS对象存储和COS对象存储都是…
阅读更多...
分享10个地推拉新和网推拉新app推广接单平台，一手接任务平台

分享10个地推拉新和网推拉新app推广接单平台，一手接任务平台

文章首推平台&#xff1a;”聚量推客“ 官方邀请码000000 从事地推、拉新、推广这一类型的工作&#xff0c;是一定要有稳定的一手接单平台的&#xff0c;因为在瞬息万变的拉新推广市场中&#xff0c;很多APP应用的推广拉新存在周期性&#xff0c;有可能这个月还在的拉新项目&a…
阅读更多...
【学习辅助】Axure手机时间管理APP原型，告别手机控高保真模板

【学习辅助】Axure手机时间管理APP原型，告别手机控高保真模板

作品概况 页面数量&#xff1a;共 30 页 兼容软件&#xff1a;Axure RP 9/10&#xff0c;不支持低版本 应用领域&#xff1a;时间管理、系统工具 作品申明&#xff1a;页面内容仅用于功能演示&#xff0c;无实际功能 作品特色 本品为「手机时间管理」APP原型&#xff0c;…
阅读更多...
动态规划题解

动态规划题解

文章目录 杨辉三角杨辉三角2爬楼梯最小花费爬楼梯斐波那契数列比特位计数不同路径 杨辉三角 var generate function(numRows) {//先定义一个空数组var ret[];//遍历行数for(let i 0;i<numRows;i){var cownew Array(i1).fill(1)//定义行内数组数&#xff0c;有多少numrows&a…
阅读更多...
基于LDA主题分析的《老友记》情景喜剧数据集的建模分析（文末送书）

基于LDA主题分析的《老友记》情景喜剧数据集的建模分析（文末送书）

&#x1f935;‍♂️ 个人主页&#xff1a;艾派森的个人主页 ✍&#x1f3fb;作者简介&#xff1a;Python学习者 &#x1f40b; 希望大家多多支持&#xff0c;我们一起进步&#xff01;&#x1f604; 如果文章对你有帮助的话&#xff0c; 欢迎评论 &#x1f4ac;点赞&#x1f4…
阅读更多...
Python字符串字母大小写变换

Python字符串字母大小写变换

嗨喽~大家好呀&#xff0c;这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 说明&#xff1a; 字符串就是一系列字符&#xff0c;在Python中用引号括起来的都是字符串&#xff0c; 引号可以是单引号&#xff0c;也可以是双引号&#xff0…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023