吴恩达《机器学习》7-1-＞7-4:过拟合问题、代价函数、线性回归的正则化、正则化的逻辑回归模型

news2024/11/20 2:30:41

一、过拟合的本质

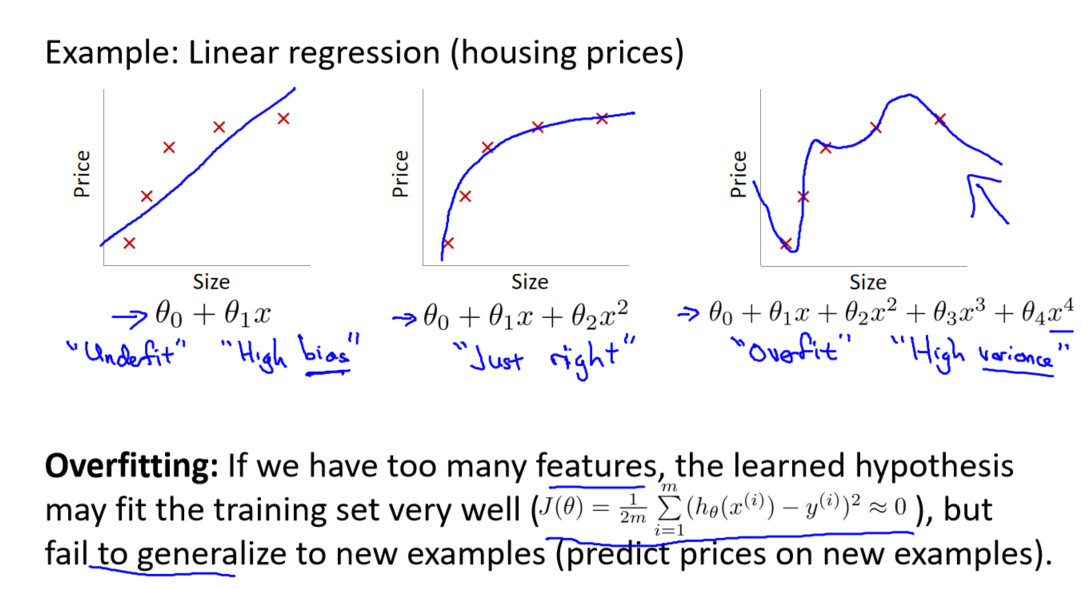
过拟合是指模型在训练集上表现良好，但在新数据上的泛化能力较差。考虑到多项式回归的例子，我们可以通过几个模型的比较来理解过拟合的本质。

线性模型（欠拟合）： 第一个模型是一个线性模型，它的拟合程度较差，不能充分适应训练集。
四次方模型（过拟合）： 第三个模型是一个四次方的模型，过于强调对训练集的拟合，失去了对新数据的泛化能力。
中间模型（适中拟合）： 中间模型似乎在拟合训练集和对新数据的泛化之间取得了平衡。

解决方案

丢弃无关特征

一种应对过拟合的方法是丢弃一些无关的特征。这可以通过手动选择保留哪些特征，或者使用一些模型选择的算法，如主成分分析（PCA）来实现。这种方法的缺点是需要人为干预，且可能遗漏一些潜在有用的特征。

正则化

另一种更普遍的方法是引入正则化技术。正则化通过保留所有特征的同时，减小参数的大小（magnitude）。这可以通过修改代价函数来实现，引入一个正则化项。正则化的核心思想是对模型复杂度进行惩罚，防止其过度拟合训练集。

二、代价函数的修改

考虑一个回归问题的模型，其中包含高次项，如：

我们知道，过多的高次项可能导致过拟合。为了避免这种情况，我们需要减小这些高次项的系数。正则化的基本思想就是在代价函数中对这些参数引入惩罚。

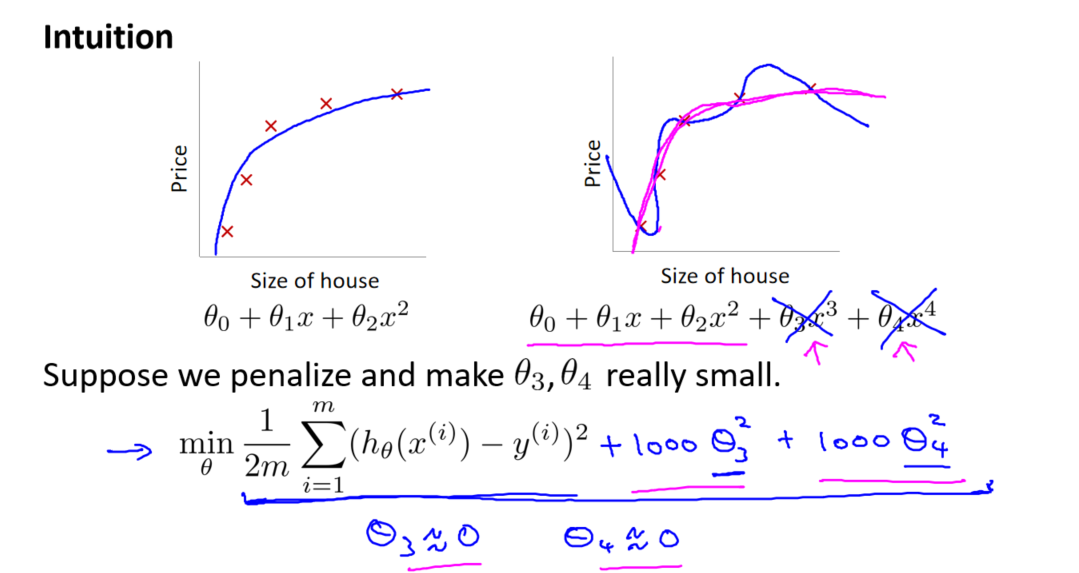
修改后的代价函数为：

其中，第一项为原始的均方误差代价，第二项是正则化项。正则化项的系数由参数 λ 决定，它是正则化参数。

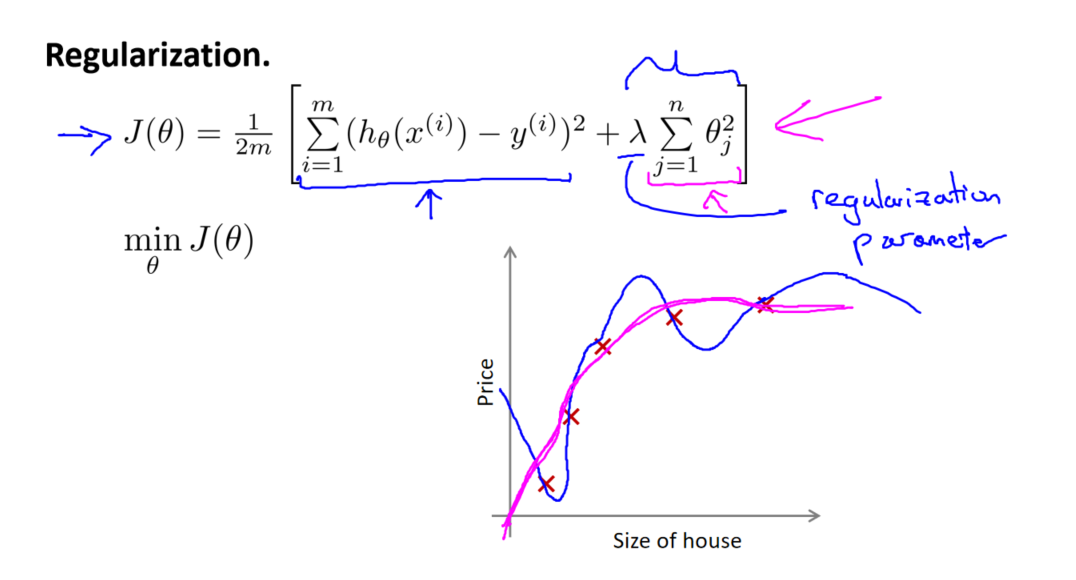
正则化的效果

通过修改代价函数，我们实现了对参数的惩罚。当 λ 较小时，正则化的影响较小，模型更趋向于原始的过拟合情况。而当 λ 较大时，正则化的惩罚力度增强，模型的复杂度降低，更趋向于简单的拟合。

通过调整 λ 的值，我们可以在模型的复杂性和泛化能力之间找到平衡点，防止过拟合的发生。

选择合适的 λ

选择合适的 λ 值是正则化中关键的一步。如果 λ 过大，模型可能会过于简化，导致欠拟合。如果 λ 过小，模型可能无法避免过拟合。

通常，可以通过交叉验证等技术来选择最优的 λ 值，使得模型在验证集上达到最佳性能。

三、正则化线性回归的代价函数

正则化线性回归的代价函数包含两部分：原始的均方误差项和正则化项。对于线性回归问题，代价函数为：

其中，第一项为原始的均方误差代价，第二项是正则化项。正则化项通过参数 λ 控制，θj 是模型的参数。

梯度下降法

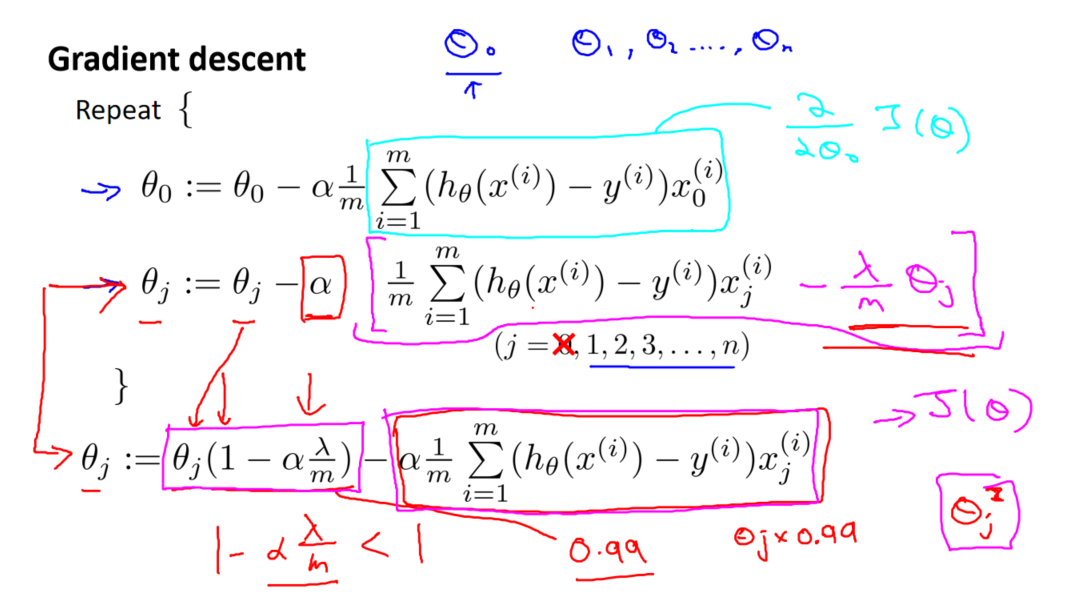
使用梯度下降法更新参数时，更新规则为：

其中，α 是学习率，m 是训练样本数量。

正规方程

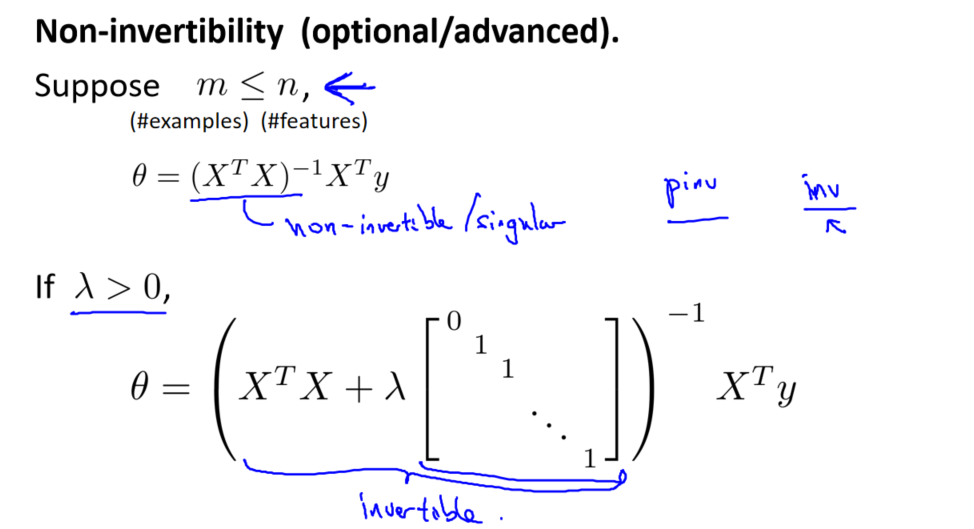
正规方程用于直接求解正则化线性回归的参数 θ。求解的公式为：

其中，X 是输入特征矩阵，y 是输出向量，L 是一个对角矩阵，对角元素为 [0,1,1,...,1][0,1,1,...,1]，与 θ0 对应的元素为 0。

梯度下降法与正规方程的比较

梯度下降法需要选择学习率 α，并进行多次迭代更新参数。正规方程则通过解析解直接计算参数，不需要选择学习率，但计算复杂度较高。通常在样本量较大时，梯度下降法更为实用；而在样本量较小且特征较多时，正规方程可能更为合适。

参数更新的影响

正则化项的引入使得参数更新时，每次都减少一个额外的值，这使得模型更趋向于简单的拟合。通过调整 λ 的值，可以控制正则化的强度，从而影响模型的复杂性和拟合效果。

四、正则化逻辑回归的代价函数

对于正则化的逻辑回归，代价函数包含两部分：原始的逻辑回归代价和正则化项。代价函数为：

其中，第一项为原始的逻辑回归代价，第二项是正则化项。正则化项通过参数 λ 控制，θj 是模型的参数。

梯度下降法

使用梯度下降法更新参数时，更新规则为：

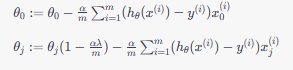
其中，α 是学习率，m 是训练样本数量。

代码示例

import numpy as np

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def costReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    m = len(X)

    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    reg = (learningRate / (2 * m)) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))

    return np.sum(first - second) / m + reg

def gradientReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    m = len(X)

    error = sigmoid(X * theta.T) - y

    grad = ((X.T * error) / m).T + (learningRate / m) * theta

    # Intercept term should not be regularized
    grad[0, 0] = grad[0, 0] - (learningRate / m) * theta[0, 0]

    return np.array(grad).ravel()