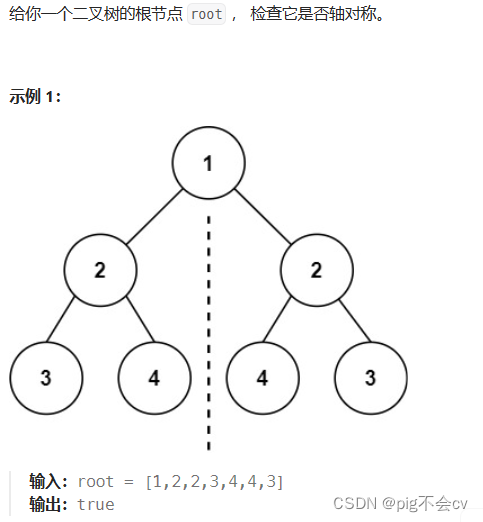
算法：

其实就是比较左右子树是否可以翻转

比较的时候：

比较外面的节点是否相等，如示例1中的节点3

比较里面的节点是否相等，如示例1中的节点4

基本思路是这样的，那怎么遍历呢？

二叉树的题一定要掌握到底用哪种遍历来解决题目，这样才能理解得更深刻！

这道题一定是后序遍历！

因为我们要搜集孩子信息，返回上一层，比如：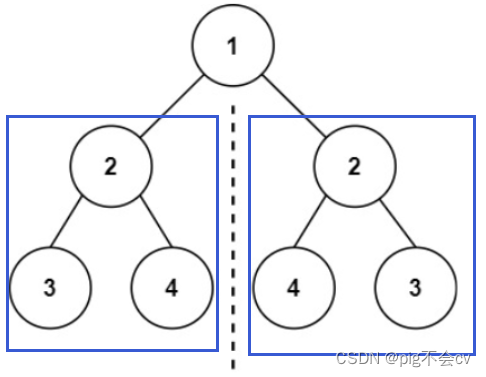

左子树：我们要搜集3（L） 4（R）的信息，返回给2

右子树：我们要搜集3（R） 4（L）的信息，返回给2

这样才能比较2.left和2.right是否对称

调试过程：

递归法：

原因：compare函数的定义不对，我定义的输入一个节点，但实际调用的是两个指针。

compare函数定义时的输入应该是两个子树,left和right

修改后还是报错了，发现是对空树的理解不对，空树被认为是对称的，而我以为不对称，改过来就好了。

正确代码：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if root == None:
            return True
        else:
            res = self.compare(root.left, root.right)
        return res
#定义一个compare函数，用来比较左右子树
#具体比较就是外面的和外面的比，里面的和里面的比
    def compare(self, left, right) -> bool:
        #排除一些绝对不对称的情况：
        if left == None and right != None:
            return False
        if right == None and left != None:
            return False
        if right == None and left == None:
            return True
        if right and left:
            outside = self.compare(left.left,right.right)
            inside = self.compare(left.right,right.left)
            issame = outside and inside
            return issame
    

时间空间复杂度：

时间复杂度：
`isSymmetric`函数会递归调用`compare`函数。在`compare`函数中，我们比较给定二叉树的左子树和右子树。由于每个节点只访问一次，时间复杂度为O(n)，其中n是二叉树中的节点数。

空间复杂度：
空间复杂度取决于递归栈的最大深度。在最坏的情况下，当二叉树是倾斜的且高度为n时，空间复杂度为O(n)。这是因为在任何时刻，递归栈最多可以容纳n个函数调用。

总体而言，时间复杂度为O(n)，空间复杂度在最坏情况下为O(n)。