题目
某组织举行会议,来了多个代表团同时到达,接待处只有一辆汽车,可以同时接待多个代表团,为了提高车辆利用率,请帮接待员计算可以坐满车的接待方案,输出方案数量。
约束:
1.一个团只能上一辆车,并且代表团人数(代表团数量小于30,每个代表团人数小于30)小于汽车容量(汽车容量小于100)
⒉.需要将车辆坐满
输入描述
第一行 :代表团人数,英文逗号隔开,代表团数量小于30,每个代表团人数小于30
第二行:汽车载客量,汽车容量小于100
输出描述
坐满汽车的方案数量
如果无解输出0
示例1:
输入
5,4,2,3,2,4,9
10
输出
4
说明
以下几种方式都可以坐满车,[2,3,5]、[2,4,4]、[2,3,5]、[2,4,4]
思路
题目翻译过来就是,在给定数组中找若干数,让他们的和等于目标值,问有多少种找法?
以示例数据为例:
输入:
5,4,2,3,2,4,9
10
记代表团人数为数组arr,长度为len,汽车载客量为total。
先将arr从小到大排序(不排序也是一样的):2 2 3 4 4 5 9
定义二维数组dp[][],dp[i][j]代表从arr的前i个数中选,使选择数的和等于j的方案数,比如:dp[0][0],代表从arr选取0个元素,让他们的和等于0有几种选法?很明显,啥都不选,和就是0,所以有1种选法,即dp[0][0]=1
dp[0][1],代表从arr选取0个元素,让他们的和等于1有几种选法?很明显,选取0个元素,要使和为1,不可能,因此dp[0][1]=0
dp[1][0],代表从arr最多选取1个元素,使他们的和等于0有几种选法?选0个元素,和等于0为选法1;选择1个元素,只能选2,大于目标0,因此不能选。所以总的选法还是为1,即dp[1][0]=1。
dp[len][total], 代表从arr最多选取len个元素(也就是从arr整个数组中选),使他们的和等于total有几种选法?也就是题目所求的答案让我们总结一般规律,对于dp[i][j]。
记录当前值cur,i为从arr选取i个元素,选取1个元素的时候为arr[0],选取i个元素的时候,应该为arr[i-1]。
如果cur>j,也就是如果选了当前元素,那么其和势必大于j(arr中全为正数),不满足,所以此时不能选当前元素,dp[i][j]=dp[i-1][j]
如果cur<=j,不选当前元素的方案数为dp[i-1][j],选了当前元素的方案数为:dp[i-1][j-cur],所以此分支总的方案数为:dp[i][j]=dp[i-1][j]+dp[i-1][j-cur]
现在有了dp的初始值和递推关系,我们可以使用动态规划求出此问题的解。
题解
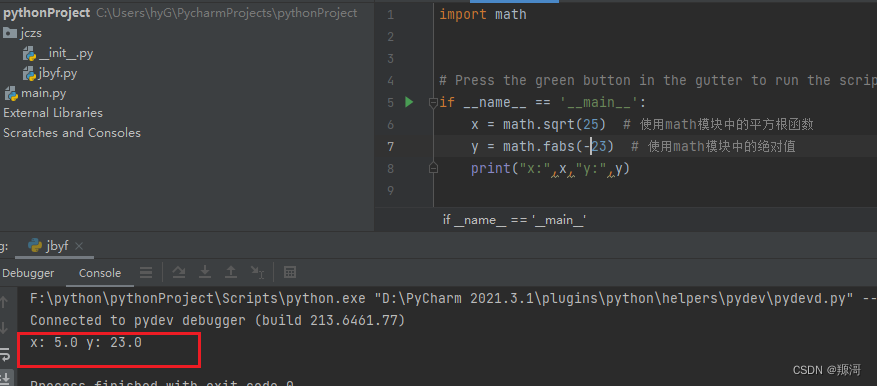
package hwod;
import java.util.Arrays;
import java.util.Scanner;
public class TakeCar {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String[] inputs = sc.nextLine().split(",");
int[] nums = Arrays.stream(inputs).mapToInt(Integer::parseInt).toArray();
int target = sc.nextInt();
System.out.println(getPlanCnt(nums, target));
}
private static int getPlanCnt(int[] nums, int target) {
int n = nums.length;
int[][] dp = new int[n + 1][target + 1];
dp[0][0] = 1;
for (int i = 1; i < n + 1; i++) {//dp[0][x],x大于0时,其值明显为0,int数组的默认值刚好为0,所以不用更新
int cur = nums[i - 1];
for (int j = 0; j < target+1; j++) {
dp[i][j] = dp[i - 1][j];
if(cur<=j) dp[i][j] += dp[i - 1][j - cur];
}
}
return dp[n][target];
}
}
说明
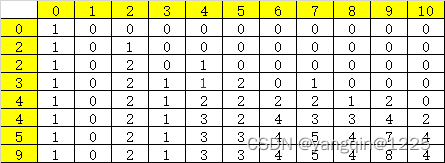
排序和不排序时,dp变化结果分别如下,可以看到最后还是得到相同的结果:4
排序:
不排序:
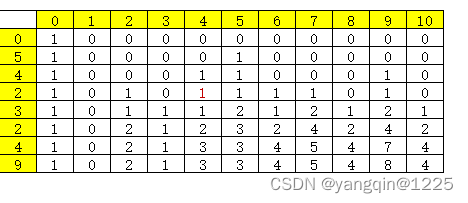
说明:标黄的,横向代表j,从0到10,纵向代表arr中第i个的值(从0开始,第0个代表不取arr的元素,为0)
推荐
如果你对本系列的其他题目感兴趣,可以参考华为OD机试真题及题解(JAVA),查看当前专栏更新的所有题目。








![Linux shell编程学习笔记23:[] [[]]的用法小结](https://img-blog.csdnimg.cn/b5369f7217264cd3bdd596e13a885b38.png)