数据结构-图的应用

news2024/6/30 0:19:41

最小生成树（最小代价树）

对于一个带权连通无向图G=(V,E)，生成树不同，每棵树的权（即树中所有边上的权值之和)也可能不同。设R为G的所有生成树的集合，若T为R中边的权值之和最小的生成树，则T称为G的最小生成树(Minimum-Spanning-Tree, MST)。
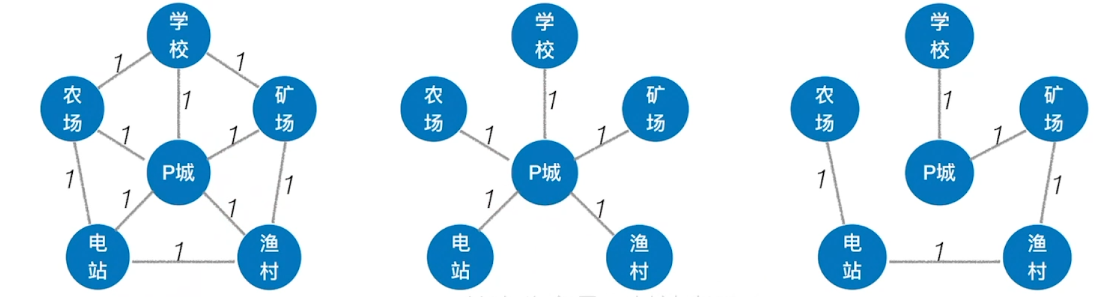
image.png

  • 最小生成树可能有多个，但边的权值之和总是唯一且最小的

  • 最小生成树的边数=顶点数一1。砍掉一条则不连通，增加一条边则会出现回路

  • 如果一个连通图本身就是―棵树，则其最小生成树就是它本身

  • 只有连通图才有生成树，非连通图只有生成森林

Prim算法（普里姆）

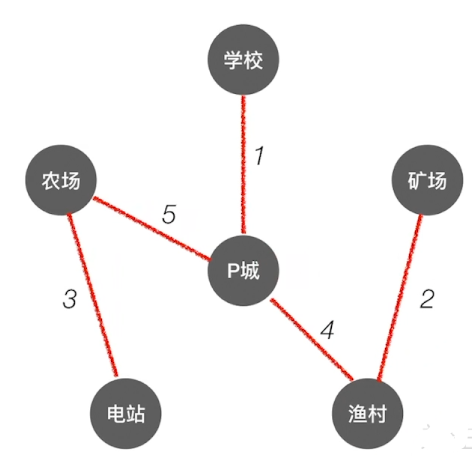
Prim 算法（普里姆):
从某一个顶点开始构建生成树;
每次将代价最小的新顶点纳入生成树，
直到所有顶点都纳入为止。
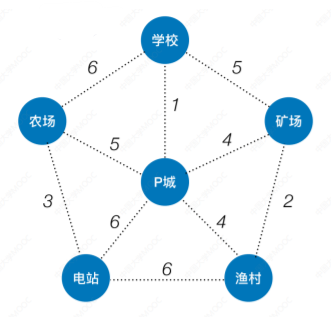
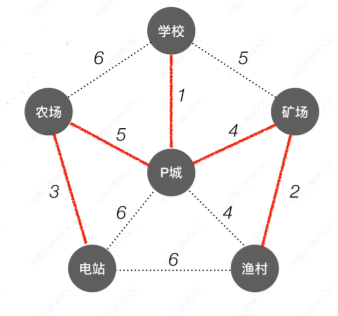
image.png
image.png
3+5+1+4+2=15
image.png
时间复杂度：O(|V|2次方）
适合用于边稠密图

Kruskal算法（克鲁斯卡尔）

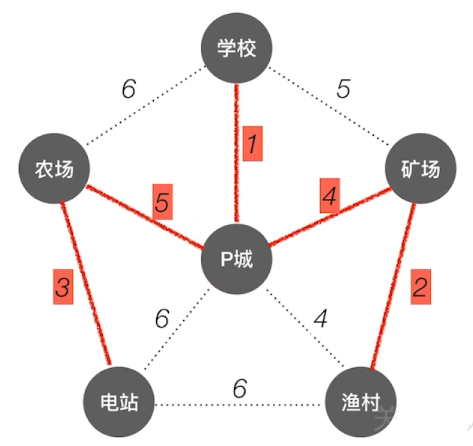
Kruskal算法(克鲁斯卡尔)
每次选择一条权值最小的边，使这条边的两头连通(原本已经连通的就不选)
直到所有结点都连通
image.png
时间复杂度：O(|E|log|E|)
适合用于边稀疏图

Prim算法的实现思想

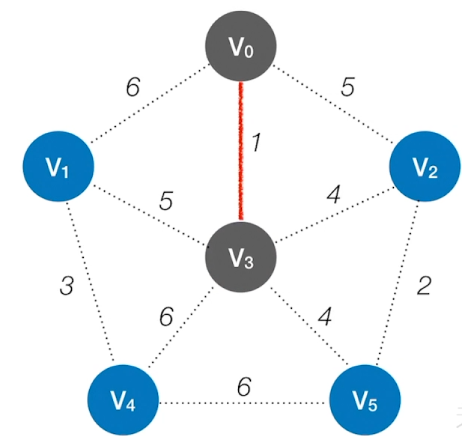
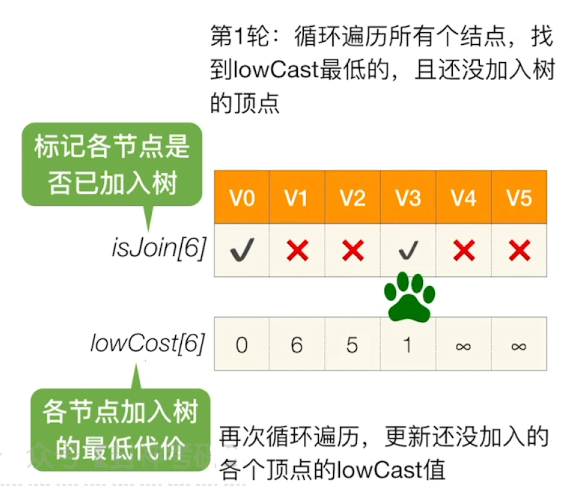
image.png
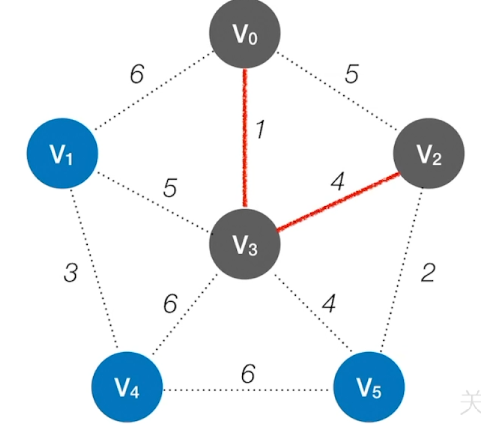
image.png

更新还没加入的各个顶点的lowCast值
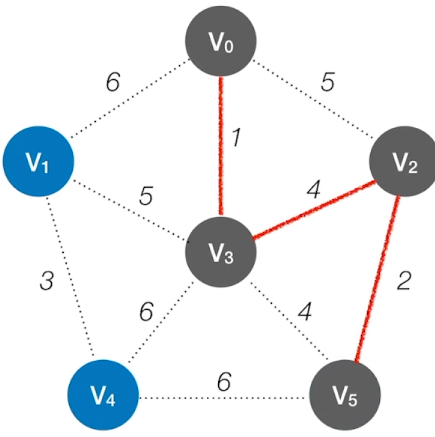
image.png

第二轮：
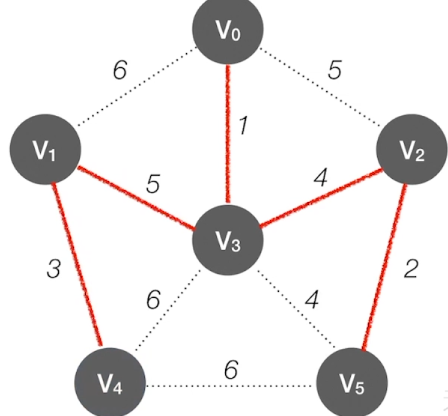
image.png
更新还没加入的各个顶点的lowCast值
image.png
image.png
第3轮：
image.png
image.png
第4轮：
image.png
image.png
第5轮：
image.png
image.png

Kruskal算法的实现思想

初始︰将各条边按权值排序
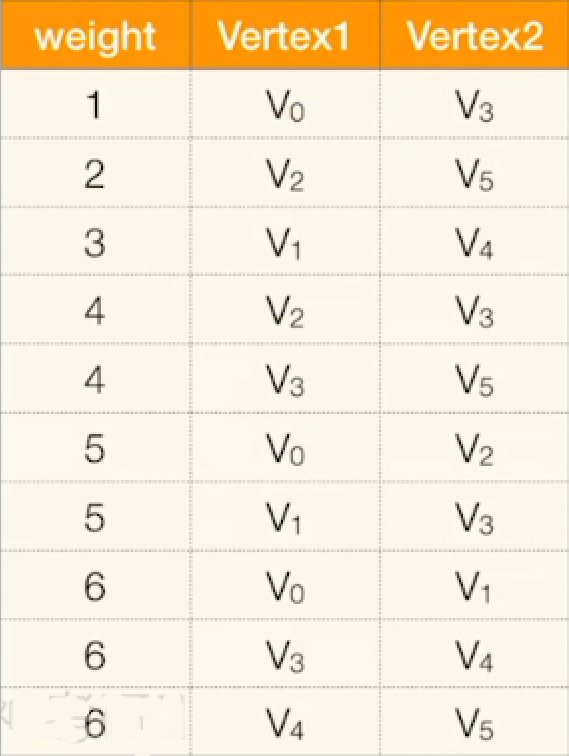
image.png
第1轮:检查第1条边的两个顶点是否连通(是否属于同一个集合)
第2轮︰检查第2条边的两个顶点是否连通(是否属于同一个集合)
第3轮︰检查第3条边的两个顶点是否连通(是否属于同一个集合)
第4轮︰检查第4条边的两个顶点是否连通(是否属于同一个集合)
第5轮︰检查第5条边的两个顶点是否连通(是否属于同一个集合)
…
每轮判断两个顶点是否属于同一集合

最短路径问题

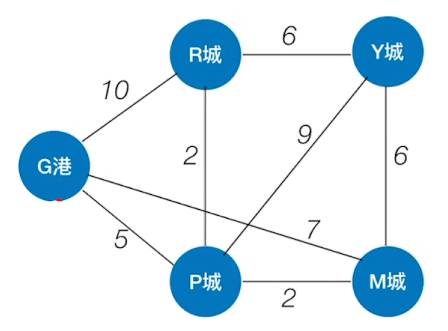
image.png
“G港”是个物流集散中心，经常需要往各个城市运东西，怎么运送距离最近？
–单源最短路径问题
各个城市之间也需要互相往来，相互之间怎么走距离最近？
–每对顶点间的最短路径

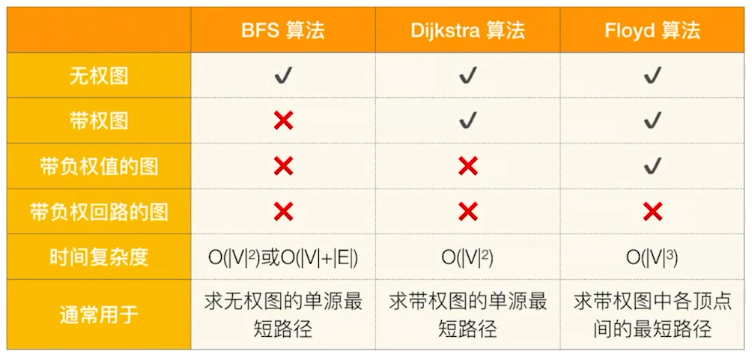
单源最短路径–BFS算法（无权图）、Dijkstra算法（带权图、无权图）
各顶点间的最短路径–Floyd算法（带权图、无权图）

BFS求无权图的单源最短路径
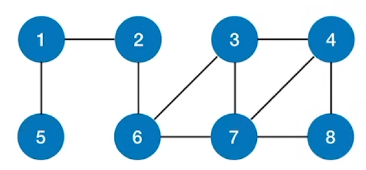
image.png

bool visited[MAX_VERTEX_NUM];//访问标记数组
//广度优先遍历
void BFS(Graph G,int v){//从顶点v出发，广度优先遍历图G
	visit(v);			//访问初始顶点v
    visited[v]=TRUE;	//对v做已访问标记
    Enqueue(Q,v);		//顶点v入队列Q
    while(!isEmpty(Q)){
        DeQueue(Q,v);	//顶点v出队列
        for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))
            //检测v所有邻接点
            if(!visited[w]){	//w为v的尚未访问的邻接顶点
                visit(w);		//访问顶点w
                visited[w]=TRUE;//对w做已访问标记
                EnQueue(Q,w);	//顶点w入队列
            }
    }
}

//求顶点u到其他顶点的最短路径
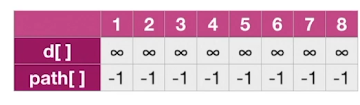
void BFS_MIN_Distance(Graph G,int v){//从顶点v出发，广度优先遍历图G
	//d[i]表示从v到i结点的最短路径
    for(i=0;i<G.vexnum;++i){
        d[i]=∞; //初始化路径长度
        path[i]=-1;//最短路径从哪个顶点过来
    }
    d[u]=0;
    visited[v]=TRUE;	//对v做已访问标记
    Enqueue(Q,v);		//顶点v入队列Q
    while(!isEmpty(Q)){
        DeQueue(Q,v);	//顶点v出队列
        for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))
            //检测v所有邻接点
            if(!visited[w]){	//w为v的尚未访问的邻接顶点
                d[w]=d[v]+1；	//路径长度加1
                path[w]=u;		//最短路径应从v到w
                visited[w]=TRUE;//对w做已访问标记
                EnQueue(Q,w);	//顶点w入队列
            }
    }
}

image.pngimage.png

最短路径问题-Dijkstra算法

Dijkstra算法
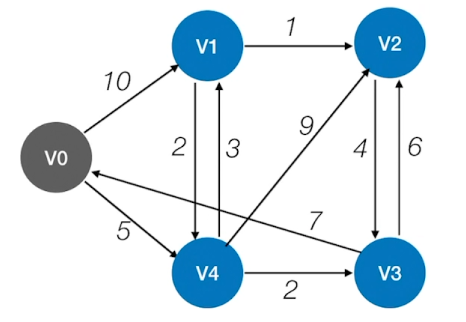
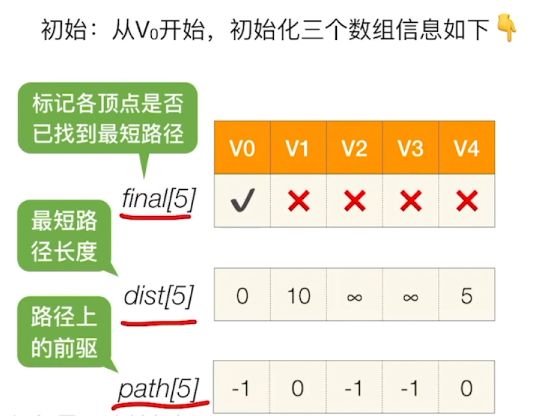
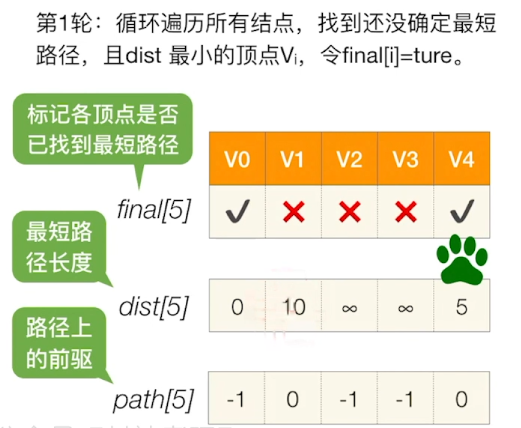
image.png
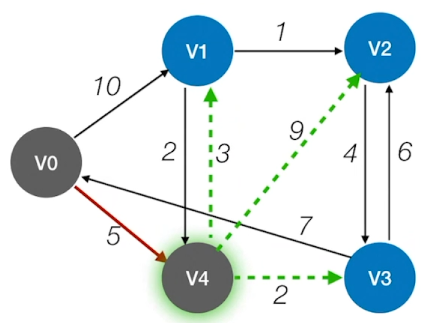
image.png
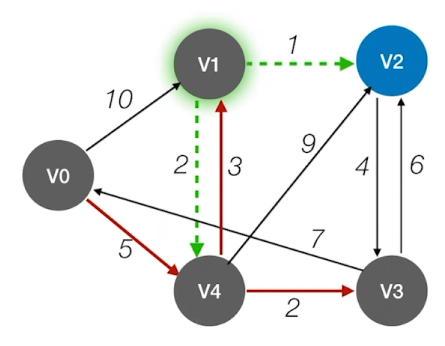
image.png
检查所有邻接自Vi的顶点，若其final值为false，则更新dist和path信息
image.png
image.png

image.png
检查所有邻接自Vi的顶点，若其final值为false，则更新dist和path信息
image.png
image.png
image.png
image.pngimage.png
V0到V2的最短（带权）路径长度为：dist[2]=9
通过path[ ]可知，V0到V2的最短（带权）路径：V0->V4->V1->V2
Dijkstra算法不适用于有负权值的带权图

最短路径-Floyd算法

Floyd算法：求出每一对顶点之间的最短路径
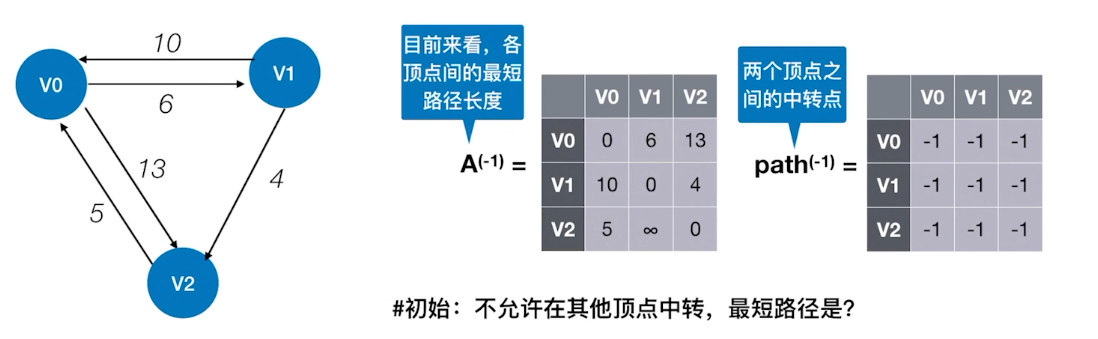
image.png
image.png
image.png
#0：若允许在V0中转，最短路径是？
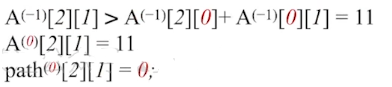
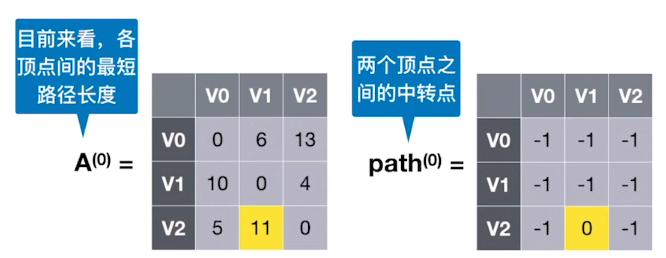
image.png
image.png
#1：若允许在V0、V1中转，最短路径是？
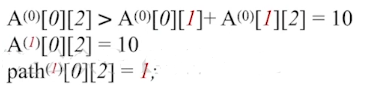
image.png
image.png
#2：若允许在V0、V1、V2中转，最短路径是？
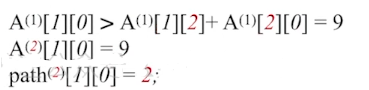
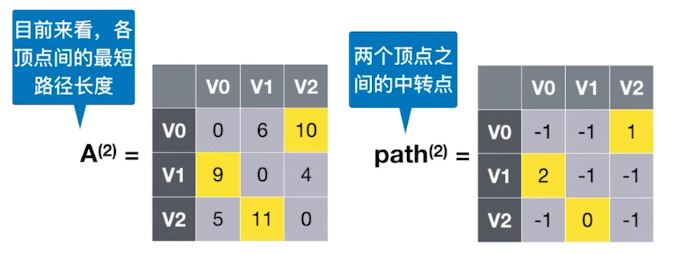
image.png
image.png
image.png
Floyd算法核心代码
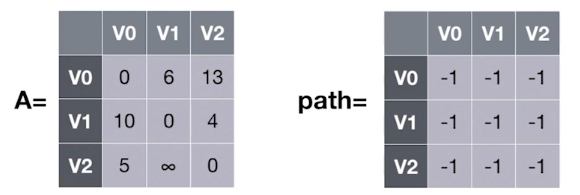
image.png

//....准备工作，根据图的信息初始化矩阵A和path
for(int k=0;k<n;k++){		//考虑以Vk作为中转点
	for(int i=0;i<n;i++){	//遍历整个矩阵，i为行号，j为列号
        for(int j=0;j<n;j++){
            if(A[i][j]>A[i][k]+A[k][j]){//以Vk为中转点的路径更短
                A[i][j]=A[i][k]+A[k][j];//更新最短路径长度
                path[i][j]=k;			//中转点
            }、
        }
    }
}

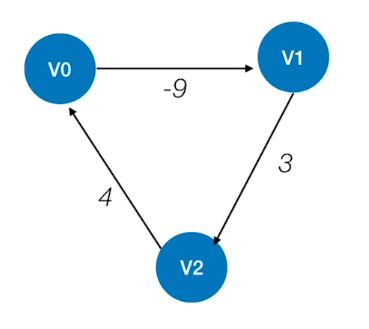
Floyd算法不能解决带有“负权回路”的图（有负权值的边组成回路），这种图有可能没有最短路径
image.png
image.png

有向无环图描述表达式

有向无环图：若一个有向图中不存在环，则称为有向无环图，简称DAG图
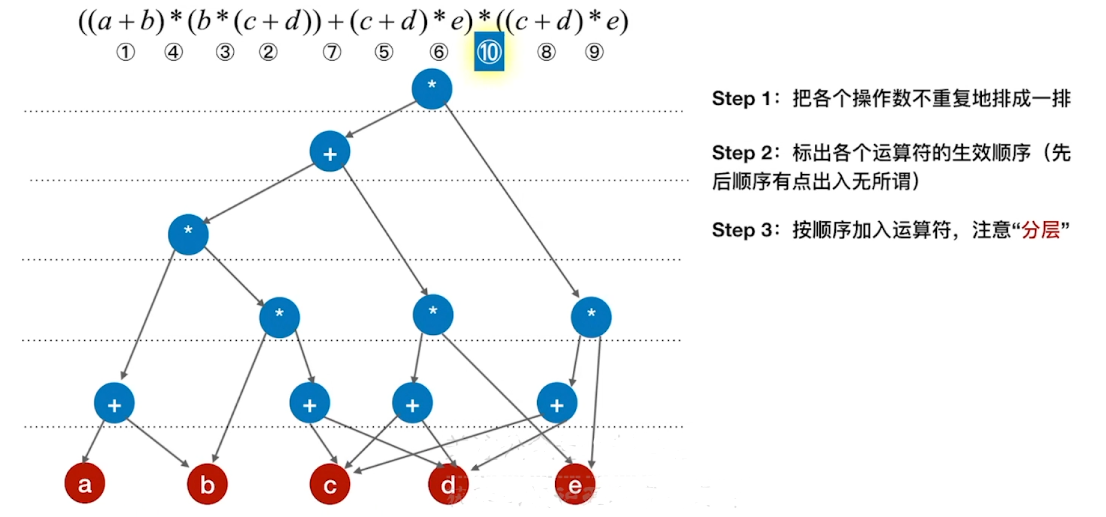
image.png
Step4:从底向上逐层检查同层的运算符是否可以合体
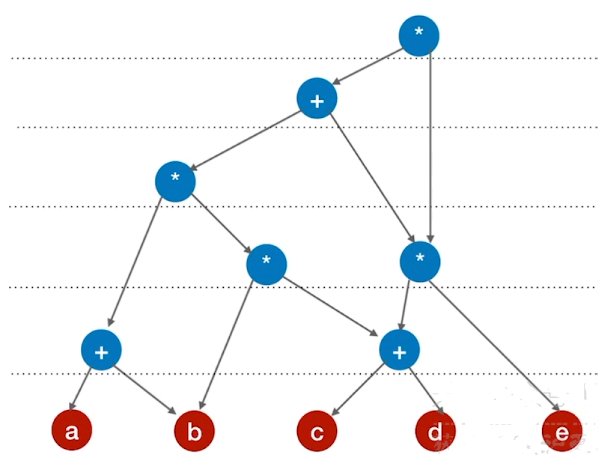
image.png

拓扑排序

AOV网
AOV网（Activity On Vertex NetWork，用顶点表示活动的网）
用DAG网（有向无环图）表示一个工程。顶点表示活动，有向边<Vi,Vj>表示活动Vi必须先语活动Vj进行
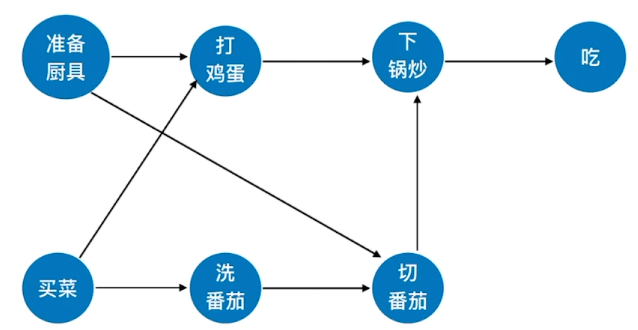
image.png
拓扑排序
image.png
拓扑排序的实现：
1：从AOV网中选择一个没有前驱（入度为0）的顶点并输出
2：从网中删除该顶点和所有以它为起点的有向边
3：重复1和2直到当前的AOV网为空或当前网中不存在无前驱的顶点为止
image.png

#define MaxVertexNum 100 //图中顶点数目的最大值
typedef struct ArcNode{  //边表结点
	int adjvex;		//该弧所指向的顶点的位置
    struct ArcNode *nextarc;	//指向下一条弧的指针
}ArcNode;
typedef struct VNode{	//顶点表结点
	VertexType data;	//顶点信息
    ArcNode *firstarc;	//指向第一条依附该顶点的弧的指针
}VNode,AdjList[MaxVertexNum];
typedef struct{
    AdjList vertices;	//邻接表
    int vexnum,arcnum;	//图的顶点数和弧数
}Graph;		//Graph是以邻接表存储的图类型
bool TopologicalSort(Graph G){
	InitStack(S);	//初始化栈，存储入度为0的顶点
    for(int i=0;i<G.vexnum;i++)
        if(indegree[i]==0)
            Push(S,i);	//将所有入度为0的顶点进栈
    int count=0;		//计数，记录当前已经输出的顶点数
    while(!isEmpty(S)){	//栈不空，则存在入度为0的顶点
        Pop(S,i);	//栈顶元素出栈
        print[count++]=i;	//输出顶点i
        for(p=G.vertices[i].firstarc;p;p=p->nextarc){
        	//将所有i指向的顶点的入度减1，并且将入度减为0的顶点压入栈s
            v=p->adjvex;
            if(!(--indegree[v]))
                Push(S,v);	//入度为0，则入栈
        }
    }
    if(count<G.vexnum)
        return false;	//排序失败，有向图中有回路
    else 
        return true;	//拓扑排序成功
}

逆拓扑排序的实现（DFS算法）

void DFSTraverse(Graph G){	//对图G进行深度优先遍历
	for(v=0;v<G.vexnum;++v)	
        visited[v]=FALSE;	//初始化已访问标记数据
    for(v=0;v<G.vexnum;++v)	//本代码中是从v=0开始遍历
        if(!visited[v])
            DFS(G,v);
}
void DFS(Graph G,int v){//从顶点v出发，深度优先遍历图G
	visited[v]=TRUE;	//设已访问标记
    for(w=FirstNeighbor(G,v);w>=0;w=NextNeighor(G,v,w))
        if(!visited[w]){	//w为u的尚未访问的邻接顶点
        DFS(G,w);
        }
    print(v);//输出顶点
}

关键路径

AOE网
在带权有向图中，以顶点表示事件，以有向边表示活动，以边上的权值表示完成该活动的开销（如完成活动所需的时间），称之为用边表示活动的网络，简称AOE网（Activity On Edge NetWork）
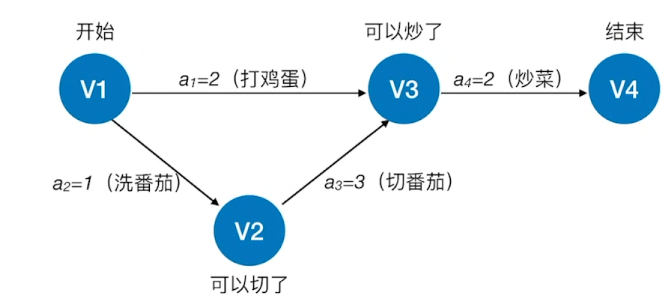
image.png
AOE网具有以下两个性质：
1：只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始
2：只有在进入某顶点的各有向边所代表的活动都已结束时，该顶点所代表的事件才能发生。
另外，有些活动是可以并行进行的。
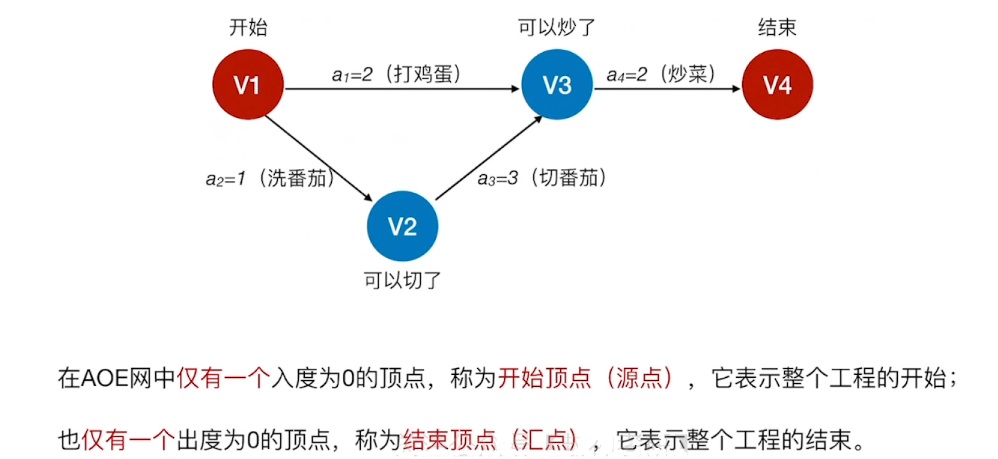
image.png

从源点到汇点的有向路径可能有多条，所有路径中，具有最大路径长度的路径称为关键路径，而把关键路径上的活动称为关键活动
完成整个工程的最短时间就是关键路径的长度，若关键活动不能按时完成，则整个工程的完成时间就会延长
image.png
求关键路径的步骤
image.png
求所有事件的最早发生时间
image.png
求所有事件的最迟发生时间
image.png
求所有活动的最早发生时间
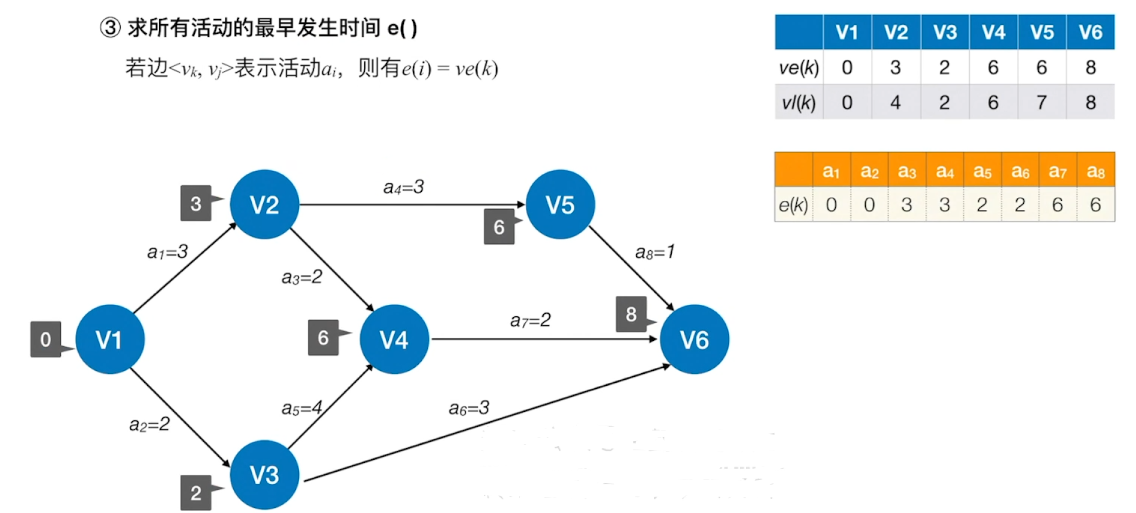
image.png
求所有活动的最迟发生时间
image.png
求所有活动的时间余量
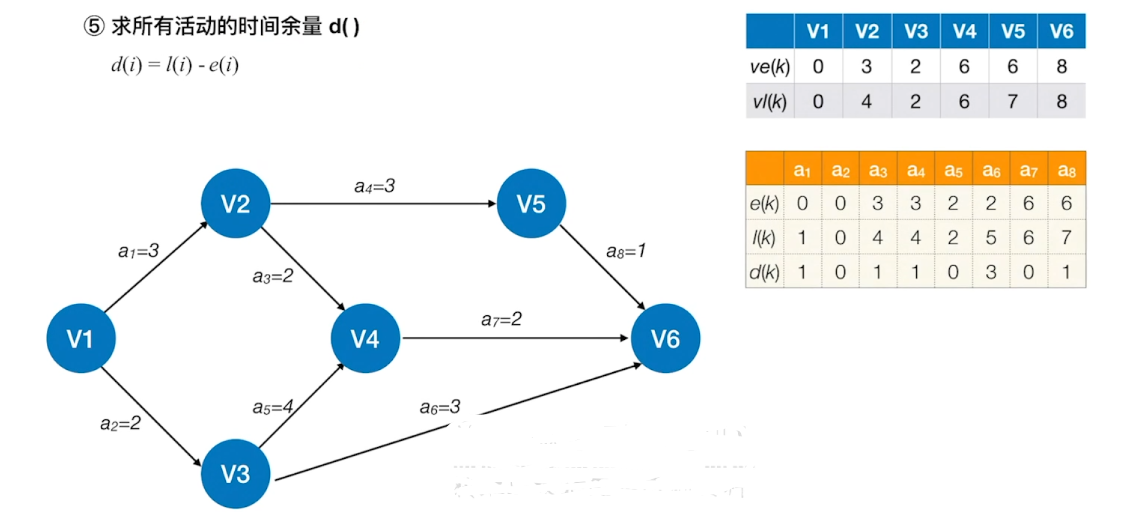
image.png
关键活动：a2、a5、a7
关键路径：V1->V3->V4->V6
关键活动、关键路径的特性
若关键活动耗时增加，则整个过程的工期将增长
缩短关键活动的时间，可以缩短整个工程的工期
当缩短到一定程度时，关键活动可能会变成非关键活动
可能有多条关键路径，只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期，只有加快那些包括在所有关键路径上的关键活动 才能达到缩短工期的目的

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1194405.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

SPI简介及FPGA通用MOSI模块实现

SPI简介及FPGA通用MOSI模块实现

简介 SPI&#xff08;Serial Peripheral Interface&#xff0c;串行外围设备接口&#xff09;通讯协议&#xff0c;是Motorola公司提出的一种同步串行接口技术。是一种高速、全双工、同步通信总线。在芯片中只占用四根管脚用来控制及数据传输。 优缺点&#xff1a; SPI通讯协…
阅读更多...
VM17虚拟机设置网络，本地使用工具连接虚拟机

VM17虚拟机设置网络，本地使用工具连接虚拟机

VM17虚拟机设置网络&#xff0c;本地使用工具连接虚拟机 下载及安装虚拟机不再说明&#xff0c;网络一堆教程。此处只对VM17设置网路及本地使用工具连接虚拟机操作&#xff0c;进行说明。 我下载的是VM17&#xff0c;网上有说VM16是较稳定的版本。想尝尝鲜&#xff0c;结果耗…
阅读更多...
linux系统源码安装php5.6手把手教程

linux系统源码安装php5.6手把手教程

linux系统源码安装php5.6实用教程 1、下载php5.6安装包2、开始安装3、安装成功 1、下载php5.6安装包 wget http://mirrors.sohu.com/php/php-5.6.2.tar.gz在安装之前&#xff0c;我们需要安装php5.6编译时所依赖的软件包。如下&#xff1a; yum -y install gcc gcc-c lib2、开…
阅读更多...
docker下的nginx代理转发到tomcat

docker下的nginx代理转发到tomcat

多次尝试失败原因&#xff0c;修改nginx配置文件以后&#xff0c;需要./nginx.sh -s reload 下&#xff0c;之前一直不转发&#xff0c;好像完全没有跳转的意思&#xff0c;后来查了多篇文档&#xff0c;最简单的方法如下 docker 安装 nginx 和tomcat就不多说了&#xff0c;可…
阅读更多...
一文6个步骤带你实现接口测试入门！

一文6个步骤带你实现接口测试入门！

一、接口测试概述 1 什么是接口测试&#xff1a; 接口测试是测试系统组件间交互的一种测试。接口测试主要用于检测外部系统与系统之间&#xff0c;内部各个子系统之间的交互点。测试的重点是要检查数据的交换&#xff0c;传递和控制管理过程&#xff0c;以及系统间的相互逻辑…
阅读更多...
CLion配置libtorch找不到xxx.dll

CLion配置libtorch找不到xxx.dll

项目场景&#xff1a; 使用CLion配置libtorch时遇到该问题 问题描述 使用CLion配置libtorch时&#xff0c;CMakeLists.txt文件写完后&#xff0c;cmake也能成功&#xff0c;但是一旦运行代码就会报错找不到xxx.dll&#xff0c;比如找不到torch_cuda.dll或找不到c10.dll 原因分…
阅读更多...
jsp基本表格和简单算法表格

jsp基本表格和简单算法表格

基本表格&#xff1b; <% page language"java" contentType"text/html; charsetUTF-8"pageEncoding"UTF-8"%><!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loose.dtd…
阅读更多...
java项目之果蔬经营平台系统（ssm框架）

java项目之果蔬经营平台系统（ssm框架）

风定落花生&#xff0c;歌声逐流水&#xff0c;大家好我是风歌&#xff0c;混迹在java圈的辛苦码农。今天要和大家聊的是一款基于ssm的果蔬经营平台系统。项目源码以及部署相关请联系风歌&#xff0c;文末附上联系信息 。 项目简介&#xff1a; 管理员&#xff1a;首页、个人…
阅读更多...
Android 12 S 系统开机流程分析-FirstStageMain（一）

Android 12 S 系统开机流程分析-FirstStageMain（一）

开机有好几种方式启动&#xff0c;本文主要讲的是按Power键开机流程。 本文参考AOSP 12原生代码&#xff0c;链接为&#xff1a;AOSP 12 Searchhttp://aospxref.com/android-12.0.0_r3/ 目录 1. BootLoader加载 2. kernel启动 3. init进程启动 3.1 FirstStageMain 3.1.1…
阅读更多...
Windows安装Docker（无网）

Windows安装Docker（无网）

Windows安装Docker&#xff08;无网&#xff09; window无网安装Docker 1. 开启虚拟化功能 1. 开启window的虚拟化功能 方式一&#xff1a;直接在window的搜索框搜索 “启用或关闭windows功能”&#xff0c;就可以快捷进入【启用或关闭windows功能】页面 方式二&#xff1…
阅读更多...
Gui基础使用之项目部署

Gui基础使用之项目部署

&#x1f3ac; 艳艳耶✌️&#xff1a;个人主页 &#x1f525; 个人专栏 &#xff1a;《Spring与Mybatis集成整合》《Vue.js使用》 ⛺️ 越努力 &#xff0c;越幸运。 1.gui图形化界面的使用 1.1 前期准备 新建仓库&#xff0c;具体操作如下&#xff1a; 初始化readme文件&…
阅读更多...
如何使用fiddler实现手机抓包，Filters过滤器！

如何使用fiddler实现手机抓包，Filters过滤器！

一、Fiddler与其他抓包工具的区别 1、Firebug虽然可以抓包&#xff0c;但是对于分析http请求的详细信息&#xff0c;不够强大。模拟http请求的功能也不够&#xff0c;且firebug常常是需要“无刷新修改”&#xff0c;如果刷新了页面&#xff0c;所有的修改都不会保存&#xff1b…
阅读更多...
ChatRule：基于知识图推理的大语言模型逻辑规则挖掘11.10

ChatRule：基于知识图推理的大语言模型逻辑规则挖掘11.10

ChatRule&#xff1a;基于知识图推理的大语言模型逻辑规则挖掘 摘要引言相关工作初始化和问题定义方法实验 摘要 逻辑规则对于揭示关系之间的逻辑联系至关重要&#xff0c;这可以提高推理性能并在知识图谱&#xff08;KG&#xff09;上提供可解释的结果。虽然已经有许多努力&a…
阅读更多...
Java类和对象详解

Java类和对象详解

文章目录 面向对象概述类和对象类定义和使用定义使用 对象引用对象的初始化和构造构造方法默认初始化就地初始化 面向对象概述 面向对象是一种现在主流的程序设计方法&#xff0c;现如今的大部分语言都支持面向对象&#xff0c;Java的面向对象是由C的面向对象衍生而来&#xf…
阅读更多...
AMD发布大小核 CPU，6核心直接砍成单核了

AMD发布大小核 CPU，6核心直接砍成单核了

2022年 Intel 第12代酷睿发布&#xff0c;PE 大小核设计被正式带到了 PC 上。 P-Core 也就是传统的大核有着高性能、高功耗&#xff0c;而 E-Core 小核则是更讲究能效比以更低频率运行。 虽说小蝾也曾有对 Windows 调度方面的怀疑&#xff0c;但多线程性能确实实打实证明了其优…
阅读更多...
node插件MongoDB（四）—— 库mongoose 操作文档使用（新增、删除、更新、查看文档）（二）

node插件MongoDB（四）—— 库mongoose 操作文档使用（新增、删除、更新、查看文档）（二）

文章目录 前言&#xff08;1&#xff09;问题&#xff1a;安装的mongoose 库版本不应该过高导致的问题&#xff08;2&#xff09;重新安装低版本 一、插入文档1. 代码2. node终端效果3. 使用mongo.exe查询数据库的内容 二、删除文档1. 删除一条2. 批量删除3. 代码 三、修改文档…
阅读更多...
react类式组件的生命周期和useEffect实现函数组件生命周期

react类式组件的生命周期和useEffect实现函数组件生命周期

概念 生命周期是一个组件丛创建,渲染,更新,卸载的过程,无论是vue还是react都具有这个设计概念,也是开发者必须熟练运用的,特别是业务开发,不同的生命周期做不同的事是很重要的. ....多说两句心得,本人是先接触vue的,无论是vue2还是vue3的生命周期,在理解和学习上都会比react更…
阅读更多...
echarts饼图label显示不全原因？

echarts饼图label显示不全原因？

echarts饼图label显示不全原因&#xff1f; 标签数量过多&#xff1a;当饼图的扇形数量较多时&#xff0c;为了保证图形的清晰性&#xff0c;ECharts 可能不会显示所有的标签&#xff0c;而是选择显示部分标签或者不显示标签。标签过长&#xff1a;如果标签的文字过长&#xf…
阅读更多...
软件测试常用的测试方法详解

软件测试常用的测试方法详解

软件测试是软件开发过程中重要组成部分&#xff0c;是用来确认一个程序的质量或者性能是否符合开发之前提出的一些要求。软件测试的目的有两方面&#xff0c;一方面是确认软件的质量&#xff0c;另一方面是提供信息&#xff0c;例如&#xff0c;给开发人员或者程序经理反馈意见…
阅读更多...
基于springboot实现家具商城管理系统项目【项目源码】计算机毕业设计

基于springboot实现家具商城管理系统项目【项目源码】计算机毕业设计

基于springboot实现家具商城管理系统演示 Java语言简介 Java是由SUN公司推出&#xff0c;该公司于2010年被oracle公司收购。Java本是印度尼西亚的一个叫做爪洼岛的英文名称&#xff0c;也因此得来java是一杯正冒着热气咖啡的标识。Java语言在移动互联网的大背景下具备了显著的…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023