一、五种算法(SWO、COA、LSO、GRO、LO)简介
1、蜘蛛蜂优化算法SWO
蜘蛛蜂优化算法(Spider wasp optimizer,SWO)由Mohamed Abdel-Basset等人于2023年提出,该算法模型雌性蜘蛛蜂的狩猎、筑巢和交配行为,具有搜索速度快,求解精度高的优势。VRPTW(MATLAB):蜘蛛蜂优化算法SWO求解带时间窗的车辆路径问题VRPTW(提供参考文献及MATLAB代码)-CSDN博客
参考文献:
[1]Abdel-Basset, M., Mohamed, R., Jameel, M. et al. Spider wasp optimizer: a novel meta-heuristic optimization algorithm. Artif Intell Rev (2023). Spider wasp optimizer: a novel meta-heuristic optimization algorithm | SpringerLink
2、小龙虾优化算法COA
小龙虾优化算法(Crayfsh optimization algorithm,COA)由Jia Heming 等人于2023年提出,该算法模拟小龙虾的避暑、竞争和觅食行为,具有搜索速度快,搜索能力强,能够有效平衡全局搜索和局部搜索的能力。多目标优化算法:基于非支配排序的小龙虾优化算法(NSCOA)MATLAB_IT猿手的博客-CSDN博客
参考文献:
[1] Jia, H., Rao, H., Wen, C. et al. Crayfish optimization algorithm. Artif Intell Rev (2023). Crayfish optimization algorithm | SpringerLink
3、光谱优化算法LSO
光谱优化算法(Light Spectrum Optimizer,LSO)由Mohamed Abdel-Basset等人于2022年提出。MD-MTSP:光谱优化算法LSO求解多仓库多旅行商问题MATLAB(可更改数据集,旅行商的数量和起点)_IT猿手的博客-CSDN博客
参考文献:
[1]Abdel-Basset M, Mohamed R, Sallam KM, Chakrabortty RK. Light Spectrum Optimizer: A Novel Physics-Inspired Metaheuristic Optimization Algorithm. Mathematics. 2022; 10(19):3466. Mathematics | Free Full-Text | Light Spectrum Optimizer: A Novel Physics-Inspired Metaheuristic Optimization Algorithm
4、淘金优化算法GRO
淘金优化算法(Gold rush optimizer,GRO)由Kamran Zolf于2023年提出,其灵感来自淘金热,模拟淘金者进行黄金勘探行为。VRPTW(MATLAB):淘金优化算法GRO求解带时间窗的车辆路径问题VRPTW(提供参考文献及MATLAB代码)-CSDN博客
参考文献:
K. Zolfi. Gold rush optimizer: A new population-based metaheuristic algorithm. Operations Research and Decisions 2023: 33(1), 113-150. DOI 10.37190/ord230108
5、狐猴优化算法
狐猴优化算法(Lemurs Optimizer,LO)由Ammar Kamal Abasi等人于2022年提出,该算法模拟狐猴的跳跃和跳舞行为,具有结构简单,思路新颖,搜索速度快等优势。单目标应用:基于狐猴优化算法(Lemurs Optimizer,LO)的微电网优化调度MATLAB_IT猿手的博客-CSDN博客
参考文献:
[1]Abasi AK, Makhadmeh SN, Al-Betar MA, Alomari OA, Awadallah MA, Alyasseri ZAA, Doush IA, Elnagar A, Alkhammash EH, Hadjouni M. Lemurs Optimizer: A New Metaheuristic Algorithm for Global Optimization. Applied Sciences. 2022; 12(19):10057. Applied Sciences | Free Full-Text | Lemurs Optimizer: A New Metaheuristic Algorithm for Global Optimization
二、模型简介
单个无人机三维路径规划问题及其建模_IT猿手的博客-CSDN博客
参考文献:
[1]胡观凯,钟建华,李永正,黎万洪.基于IPSO-GA算法的无人机三维路径规划[J].现代电子技术,2023,46(07):115-120
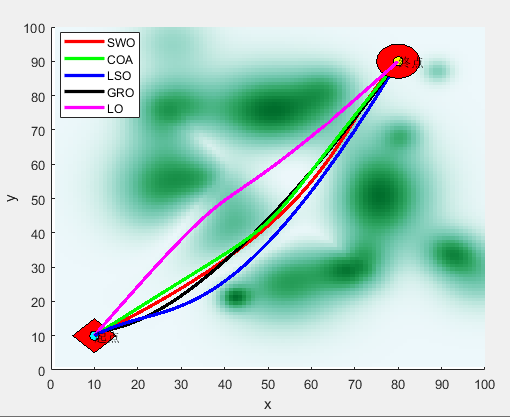
三、SWO、COA、LSO、GRO、LO求解无人机路径规划
(1)部分代码
close all
clear
clc
、warning off;
%% 三维路径规划模型定义
global startPos goalPos N
N=2;%待优化点的个数(可以修改)
startPos = [10, 10, 80]; %起点(可以修改)
goalPos = [80, 90, 150]; %终点(可以修改)
SearchAgents_no=30; % 种群大小(可以修改)
Function_name='F1'; %F1:随机产生地图 F2:导入固定地图
Max_iteration=100; %最大迭代次数(可以修改)
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
AlgorithmName={'SWO','COA','LSO','GRO','LO'};%算法名称
addpath('./AlgorithmCode/')%添加算法路径
bestFit=[];%保存各算法的最优适应度值
for i=1:size(AlgorithmName,2)%遍历每个算法,依次求解当前问题
Algorithm=str2func(AlgorithmName{i});%获取当前算法名称,并将字符转换为函数
[Best_score,Best_pos,Convergence_curve]=Algorithm(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);%当前算法求解
%将当前算法求解结果放入data中
data(i).Best_score=Best_score;%保存该算法的Best_score到data
data(i).Best_pos=Best_pos;%保存该算法的Best_pos到data
data(i).Convergence_curve=Convergence_curve;%保存该算法的Convergence_curve到data
bestFit=[bestFit data(i).Best_score];
end
%% 画各算法的直方图
figure
bar(bestFit)
ylabel('无人机飞行路径长度');
set(gca,'xtick',1:1:size(AlgorithmName,2));
set(gca,'XTickLabel',AlgorithmName)
saveas(gcf,'./Picture/直方图.jpg') %将图片保存到Picture文件夹下面
%% 画收敛曲线
strColor={'r-','g-','b-','k-','m-','c-','y-'};
figure
for i=1:size(data,2)
plot(data(i).Convergence_curve,strColor{i},'linewidth',1.5)%semilogy
hold on
end
xlabel('迭代次数');
ylabel('无人机飞行路径长度');
legend(AlgorithmName,'Location','Best')
saveas(gcf,'./Picture/收敛曲线.jpg') %将图片保存到Picture文件夹下面
%% 显示三维图并保存
path=plotFigure(data,AlgorithmName,strColor);%path是各算法求解的无人机路径
saveas(gcf,'./Picture/路径曲线(三维).jpg') %将图片保存到Picture文件夹下面
%% 显示二维图并保存
view(2)
saveas(gcf,'./Picture/路径曲线(二维).jpg') %将图片保存到Picture文件夹下面
(2)部分结果