广度优先搜索理论基础

广搜的搜索方式就适合于解决两个点之间的最短路径问题。因为广搜是从起点出发，以起始点为中心一圈一圈进行搜索，一旦遇到终点，记录之前走过的节点就是一条最短路。
广搜是一圈一圈的遍历方式，如下图：

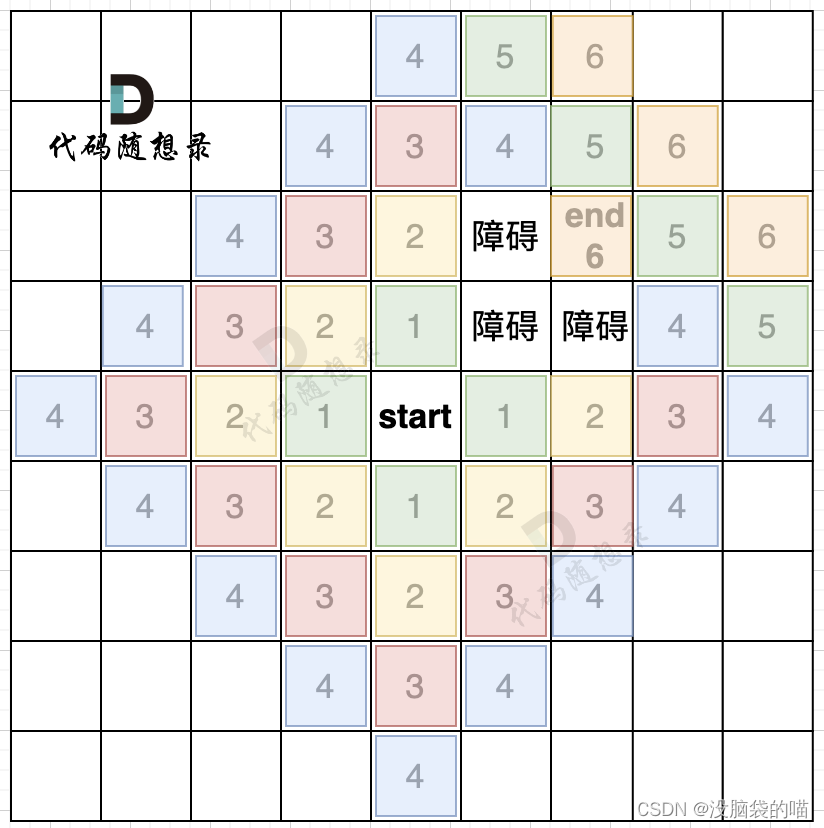
遍历可以是用队列，还是用栈，甚至用数组实现。以下是使用队列实现的模板：

//方向数组
 //上(0,1)
 //右(1,0)
 //左(-1,0)
 //下(0,-1)
public int dir[][]={{0,1},{1,0},{-1,0},{0,-1}};
//用于记录是否走过
public boolean[][] visited;
public void bfs(char[][] grid,int x,int y){
        //使用栈实现节点遍历
        Queue<int[]> queue = new LinkedList<>();
        queue.offer(new int[]{x,y});
        visited[x][y]=true;
        while(!queue.isEmpty()){
            int [] node=queue.poll();
            //像四个方向移动
            int nodex=node[0];
            int nodey=node[1];
            for(int i=0;i<4;i++){
                int nextx=nodex+dir[i][0];
                int nexty=nodey+dir[i][1];
                //边界判断
                if(nextx<0||nextx>=grid.length||nexty<0||nexty>=grid[0].length){
                    continue;
                }
                //入栈并标记
                if(visited[nextx][nexty]==false){
                    queue.offer(new int[]{nextx,nexty});
                    visited[nextx][nexty]=true;
                }
            }
        }
    }

岛屿数量

广搜版

class Solution {
    //上(0,1)
    //右(1,0)
    //左(-1,0)
    //下(0,-1)
    public int dir[][]={{0,1},{1,0},{-1,0},{0,-1}};
    public boolean[][] visited;
    public int numIslands(char[][] grid) {
        //标记是否走过
        visited=new boolean[grid.length][grid[0].length];
        int res=0;
        for(int p=0;p<grid.length;p++){
            for(int q=0;q<grid[0].length;q++){
                if(grid[p][q]=='1'&&!visited[p][q]){
                   oneoflands(grid,p,q);
                   res++; 
                }
            }
        }
        return res;
    }
    public void oneoflands(char[][] grid,int x,int y){
        //使用栈实现节点遍历
        Queue<int[]> queue = new LinkedList<>();
        queue.offer(new int[]{x,y});
        visited[x][y]=true;
        while(!queue.isEmpty()){
            int [] node=queue.poll();
            //像四个方向移动
            int nodex=node[0];
            int nodey=node[1];
            for(int i=0;i<4;i++){
                int nextx=nodex+dir[i][0];
                int nexty=nodey+dir[i][1];
                //边界判断
                if(nextx<0||nextx>=grid.length||nexty<0||nexty>=grid[0].length){
                    continue;
                }
                //入栈
                if(grid[nextx][nexty]=='1'&&visited[nextx][nexty]==false){
                    queue.offer(new int[]{nextx,nexty});
                    visited[nextx][nexty]=true;
                }
            }
        }
    }
}

深搜版

class Solution {
    boolean[][] visited;
    int dir[][] = {
        {0, 1}, //right
        {1, 0}, //down
        {-1, 0}, //up
        {0, -1} //left
    };
    public int numIslands(char[][] grid) {
        int count = 0;
        visited = new boolean[grid.length][grid[0].length];

        for(int i = 0; i < grid.length; i++){
            for(int j = 0; j < grid[0].length; j++){
                if(visited[i][j] == false && grid[i][j] == '1'){
                    count++;
                    dfs(grid, i, j);
                }
            }
        }
        return count;
    }

    private void dfs(char[][]grid, int x, int y){
        if(visited[x][y] == true || grid[x][y] == '0')
            return;
	    
        visited[x][y] = true;
	
        for(int i = 0; i < 4; i++){
            int nextX = x + dir[i][0];
            int nextY = y + dir[i][1];
            if(nextX < 0 || nextY < 0 || nextX >= grid.length || nextY >= grid[0].length)
                continue;
            //当前节点满足条件 使用递归标记当前节点的周围节点
            dfs(grid, nextX, nextY);
        }
    }
}