文章目录
- denoising matching term
- σ t z \sigma_tz σtz的猜想
- Diffusion Model for Speech
- Diffusion Model for Text
- Mask-Predict
部分截图来自原课程视频《2023李宏毅最新生成式AI教程》,B站自行搜索。
书接上文。
denoising matching term
E
q
(
x
t
∣
x
0
)
[
D
K
L
(
q
(
x
t
−
1
∣
x
t
,
x
0
)
∣
∣
p
θ
(
x
t
−
1
∣
x
t
)
)
]
E_{q(x_t|x_0)}\left[D_{KL}({q(x_{t-1}|x_t,x_0)}||p_\theta(x_{t-1}|x_t)) \right]
Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))]
这个式子还是很复杂,先来关注中间部分:
q
(
x
t
−
1
∣
x
t
,
x
0
)
q(x_{t-1}|x_t,x_0)
q(xt−1∣xt,x0)
其含义是已知清晰的图片
x
0
x_0
x0和经过
t
t
t个Denoise步骤后
x
t
x_t
xt的情况下,其中间某个Denoise后的分布
x
t
−
1
x_{t-1}
xt−1

上面的原理那节中已经知道下面三个式子的计算方法:
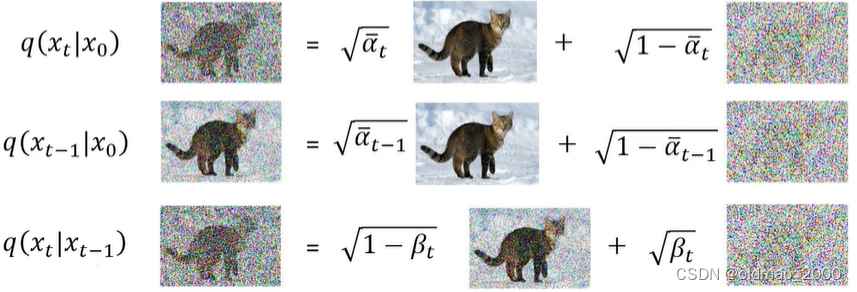
现在的思路就是要把不会计算的式子用已知的式子表达出来。
q
(
x
t
−
1
∣
x
t
,
x
0
)
=
q
(
x
t
−
1
,
x
t
,
x
0
)
q
(
x
t
,
x
0
)
=
q
(
x
t
∣
x
t
−
1
,
x
0
)
q
(
x
t
−
1
∣
x
0
)
q
(
x
0
)
q
(
x
t
∣
x
0
)
q
(
x
0
)
=
q
(
x
t
∣
x
t
−
1
,
x
0
)
q
(
x
t
−
1
∣
x
0
)
q
(
x
t
∣
x
0
)
\begin{align*}q(x_{t-1}|x_t,x_0)&=\cfrac{q(x_{t-1},x_t,x_0)}{q(x_t,x_0)}\\ &=\cfrac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)\cancel{q(x_0)}}{q(x_t|x_0)\cancel{q(x_0)}}\\ &=\cfrac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}\end{align*}
q(xt−1∣xt,x0)=q(xt,x0)q(xt−1,xt,x0)=q(xt∣x0)q(x0)
q(xt∣xt−1,x0)q(xt−1∣x0)q(x0)
=q(xt∣x0)q(xt∣xt−1,x0)q(xt−1∣x0)
上式中的三个q都是搞屎分布,而且三个分布的均值和Var都已知(看上面图片),下面就是原论文的推导:
q
(
x
t
−
1
∣
x
t
,
x
0
)
=
q
(
x
t
∣
x
t
−
1
,
x
0
)
q
(
x
t
−
1
∣
x
0
)
q
(
x
t
∣
x
0
)
=
N
(
x
t
;
α
t
x
t
−
1
,
(
1
−
α
t
)
I
)
N
(
x
t
−
1
;
α
ˉ
t
−
1
x
0
,
(
1
−
α
ˉ
t
−
1
)
I
)
N
(
x
t
;
α
ˉ
t
x
0
,
(
1
−
α
ˉ
t
)
I
)
∝
exp
{
−
[
(
x
t
−
α
t
x
t
−
1
)
2
2
(
1
−
α
t
)
+
(
x
t
−
1
−
α
ˉ
t
−
1
x
0
)
2
2
(
1
−
α
ˉ
t
−
1
)
−
(
x
t
−
α
ˉ
t
x
0
)
2
2
(
1
−
α
ˉ
t
)
]
}
=
exp
{
−
1
2
[
(
x
t
−
α
t
x
t
−
1
)
2
1
−
α
t
+
(
x
t
−
1
−
α
ˉ
t
−
1
x
0
)
2
1
−
α
ˉ
t
−
1
−
(
x
t
−
α
ˉ
t
x
0
)
2
1
−
α
ˉ
t
]
}
=
exp
{
−
1
2
[
(
−
2
α
t
x
t
x
t
−
1
+
α
t
x
t
−
1
2
)
1
−
α
t
+
(
x
t
−
1
2
−
2
α
ˉ
t
−
1
x
t
−
1
x
0
)
1
−
α
ˉ
t
−
1
+
C
(
x
t
,
x
0
)
]
}
∝
exp
{
−
1
2
[
−
2
α
t
x
t
x
t
−
1
1
−
α
t
+
α
t
x
t
−
1
2
1
−
α
t
+
x
t
−
1
2
1
−
α
ˉ
t
−
1
−
2
α
ˉ
t
−
1
x
t
−
1
x
0
1
−
α
ˉ
t
−
1
]
}
=
exp
{
−
1
2
[
(
α
t
1
−
α
t
+
1
1
−
α
ˉ
t
−
1
)
x
t
−
1
2
−
2
(
α
t
x
t
1
−
α
t
+
α
ˉ
t
−
1
x
0
1
−
α
ˉ
t
−
1
)
x
t
−
1
]
}
=
exp
{
−
1
2
[
α
t
(
1
−
α
ˉ
t
−
1
)
+
1
−
α
t
(
1
−
α
t
)
(
1
−
α
ˉ
t
−
1
)
x
t
−
1
2
−
2
(
α
t
x
t
1
−
α
t
+
α
ˉ
t
−
1
x
0
1
−
α
ˉ
t
−
1
)
x
t
−
1
]
}
=
exp
{
−
1
2
[
α
t
−
α
ˉ
t
+
1
−
α
t
(
1
−
α
t
)
(
1
−
α
ˉ
t
−
1
)
x
t
−
1
2
−
2
(
α
t
x
t
1
−
α
t
+
α
ˉ
t
−
1
x
0
1
−
α
ˉ
t
−
1
)
x
t
−
1
]
}
=
exp
{
−
1
2
[
1
−
α
ˉ
t
(
1
−
α
t
)
(
1
−
α
ˉ
t
−
1
)
x
t
−
1
2
−
2
(
α
t
x
t
1
−
α
t
+
α
ˉ
t
−
1
x
0
1
−
α
ˉ
t
−
1
)
x
t
−
1
]
}
=
exp
{
−
1
2
(
1
−
α
ˉ
t
(
1
−
α
t
)
(
1
−
α
ˉ
t
−
1
)
)
[
x
t
−
1
2
−
2
(
α
t
x
t
1
−
α
t
+
α
ˉ
t
−
1
x
0
1
−
α
ˉ
t
−
1
)
1
−
α
ˉ
t
(
1
−
α
t
)
(
1
−
α
ˉ
t
−
1
)
x
t
−
1
]
}
=
exp
{
−
1
2
(
1
−
α
ˉ
t
(
1
−
α
t
)
(
1
−
α
ˉ
t
−
1
)
)
[
x
t
−
1
2
−
2
(
α
t
x
t
1
−
α
t
+
α
ˉ
t
−
1
x
0
1
−
α
ˉ
t
−
1
)
(
1
−
α
t
)
(
1
−
α
ˉ
t
−
1
)
1
−
α
ˉ
t
x
t
−
1
]
}
=
exp
{
−
1
2
(
1
(
1
−
α
t
)
(
1
−
α
ˉ
t
−
1
)
1
−
α
ˉ
t
)
[
x
t
−
1
2
−
2
(
α
t
x
t
1
−
α
t
+
α
ˉ
t
−
1
x
0
1
−
α
ˉ
t
−
1
)
(
1
−
α
t
)
(
1
−
α
ˉ
t
−
1
)
1
−
α
ˉ
t
x
t
−
1
]
}
∝
N
(
x
t
−
1
;
α
t
(
1
−
α
ˉ
t
−
1
)
x
t
+
α
ˉ
t
−
1
(
1
−
α
t
)
x
0
1
−
α
ˉ
t
⏟
μ
q
(
x
t
,
x
0
)
,
(
1
−
α
t
)
(
1
−
α
ˉ
t
−
1
)
1
−
α
ˉ
t
I
⏟
∑
q
(
t
)
)
\begin{align*} q(x_{t-1}|x_t,x_0)&=\cfrac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}\\ &=\cfrac{\mathcal{N}(x_t;\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)\mathrm{I})\mathcal{N}(x_{t-1};\sqrt{\bar\alpha_{t-1}}x_0,(1-\bar\alpha_{t-1})\mathrm{I}) }{\mathcal{N}(x_t;\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)\mathrm{I})}\\ &\propto \exp \left \{-\left[\cfrac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{2(1-\alpha_t)} + \cfrac{(x_{t-1}-\sqrt{\bar\alpha_{t-1}}x_0)^2}{2(1-\bar\alpha_{t-1})} - \cfrac{(x_t-\sqrt{\bar\alpha_t}x_0)^2}{2(1-\bar\alpha_t)}\right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\cfrac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{1-\alpha_t} + \cfrac{(x_{t-1}-\sqrt{\bar\alpha_{t-1}}x_0)^2}{1-\bar\alpha_{t-1}} - \cfrac{(x_t-\sqrt{\bar\alpha_t}x_0)^2}{1-\bar\alpha_t}\right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\cfrac{(-2\sqrt{\alpha_t}x_tx_{t-1}+\alpha_tx_{t-1}^2)}{1-\alpha_t} + \cfrac{(x_{t-1}^2-2\sqrt{\bar\alpha_{t-1}}x_{t-1}x_0)}{1-\bar\alpha_{t-1}} + C(x_t,x_0)\right] \right \}\\ &\propto \exp \left \{-\cfrac{1}{2}\left[-\cfrac{2\sqrt{\alpha_t}x_tx_{t-1}}{1-\alpha_t}+\cfrac{\alpha_tx_{t-1}^2}{1-\alpha_t} + \cfrac{x_{t-1}^2}{1-\bar\alpha_{t-1}} - \cfrac{2\sqrt{\bar\alpha_{t-1}}x_{t-1}x_0}{1-\bar\alpha_{t-1}} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\left(\cfrac{\alpha_t}{1-\alpha_t} + \cfrac{1}{1-\bar\alpha_{t-1}} \right)x_{t-1}^2 - 2\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\cfrac{\alpha_t(1-\bar\alpha_{t-1})+1-\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}x_{t-1}^2 - 2\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\cfrac{\alpha_t-\bar\alpha_t+1-\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}x_{t-1}^2 - 2\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left[\cfrac{1-\bar\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}x_{t-1}^2 - 2\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left(\cfrac{1-\bar\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}\right)\left[x_{t-1}^2 - 2\cfrac{\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)}{\cfrac{1-\bar\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}}x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left(\cfrac{1-\bar\alpha_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})}\right)\left[x_{t-1}^2 - 2\cfrac{\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_{t-1} \right] \right \}\\ &=\exp \left \{-\cfrac{1}{2}\left(\cfrac{1}{\cfrac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}}\right)\left[x_{t-1}^2 - 2\cfrac{\left(\cfrac{\sqrt{\alpha_t}x_t}{1-\alpha_t} + \cfrac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}} \right)(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_{t-1} \right] \right \}\\ &\propto \mathcal{N}\left(x_{t-1;} \underset{\mu_q(x_t,x_0)}{\underbrace{\cfrac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}(1-\alpha_t)x_0}{1-\bar\alpha_t}}},\underset{\sum_q(t)}{\underbrace{\cfrac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}\mathrm{I}}}\right) \end{align*}
q(xt−1∣xt,x0)=q(xt∣x0)q(xt∣xt−1,x0)q(xt−1∣x0)=N(xt;αˉtx0,(1−αˉt)I)N(xt;αtxt−1,(1−αt)I)N(xt−1;αˉt−1x0,(1−αˉt−1)I)∝exp{−[2(1−αt)(xt−αtxt−1)2+2(1−αˉt−1)(xt−1−αˉt−1x0)2−2(1−αˉt)(xt−αˉtx0)2]}=exp{−21[1−αt(xt−αtxt−1)2+1−αˉt−1(xt−1−αˉt−1x0)2−1−αˉt(xt−αˉtx0)2]}=exp{−21[1−αt(−2αtxtxt−1+αtxt−12)+1−αˉt−1(xt−12−2αˉt−1xt−1x0)+C(xt,x0)]}∝exp{−21[−1−αt2αtxtxt−1+1−αtαtxt−12+1−αˉt−1xt−12−1−αˉt−12αˉt−1xt−1x0]}=exp{−21[(1−αtαt+1−αˉt−11)xt−12−2(1−αtαtxt+1−αˉt−1αˉt−1x0)xt−1]}=exp{−21[(1−αt)(1−αˉt−1)αt(1−αˉt−1)+1−αtxt−12−2(1−αtαtxt+1−αˉt−1αˉt−1x0)xt−1]}=exp{−21[(1−αt)(1−αˉt−1)αt−αˉt+1−αtxt−12−2(1−αtαtxt+1−αˉt−1αˉt−1x0)xt−1]}=exp{−21[(1−αt)(1−αˉt−1)1−αˉtxt−12−2(1−αtαtxt+1−αˉt−1αˉt−1x0)xt−1]}=exp⎩
⎨
⎧−21((1−αt)(1−αˉt−1)1−αˉt)
xt−12−2(1−αt)(1−αˉt−1)1−αˉt(1−αtαtxt+1−αˉt−1αˉt−1x0)xt−1
⎭
⎬
⎫=exp⎩
⎨
⎧−21((1−αt)(1−αˉt−1)1−αˉt)
xt−12−21−αˉt(1−αtαtxt+1−αˉt−1αˉt−1x0)(1−αt)(1−αˉt−1)xt−1
⎭
⎬
⎫=exp⎩
⎨
⎧−21
1−αˉt(1−αt)(1−αˉt−1)1
xt−12−21−αˉt(1−αtαtxt+1−αˉt−1αˉt−1x0)(1−αt)(1−αˉt−1)xt−1
⎭
⎬
⎫∝N
xt−1;μq(xt,x0)
1−αˉtαt(1−αˉt−1)xt+αˉt−1(1−αt)x0,∑q(t)
1−αˉt(1−αt)(1−αˉt−1)I
经过以上的推导,得到以下结论:
q
(
x
t
−
1
∣
x
t
,
x
0
)
q(x_{t-1}|x_t,x_0)
q(xt−1∣xt,x0)仍然是一个高斯分布,其Mean为:
α
t
(
1
−
α
ˉ
t
−
1
)
x
t
+
α
ˉ
t
−
1
(
1
−
α
t
)
x
0
1
−
α
ˉ
t
=
α
t
(
1
−
α
ˉ
t
−
1
)
x
t
+
α
ˉ
t
−
1
β
t
x
0
1
−
α
ˉ
t
\cfrac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}(1-\alpha_t)x_0}{1-\bar\alpha_t}=\cfrac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}\beta_tx_0}{1-\bar\alpha_t}
1−αˉtαt(1−αˉt−1)xt+αˉt−1(1−αt)x0=1−αˉtαt(1−αˉt−1)xt+αˉt−1βtx0
看分子大概意思就是中间步骤
x
t
−
1
x_{t-1}
xt−1是由
x
0
x_0
x0和
x
t
x_t
xt按某个权重比例进行融合而成。
Variance为:
(
1
−
α
t
)
(
1
−
α
ˉ
t
−
1
)
1
−
α
ˉ
t
I
=
1
−
α
ˉ
t
−
1
1
−
α
ˉ
t
β
t
I
\cfrac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}\mathrm{I}=\cfrac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t\mathrm{I}
1−αˉt(1−αt)(1−αˉt−1)I=1−αˉt1−αˉt−1βtI
接下来考虑最小化denoising matching term
E
q
(
x
t
∣
x
0
)
[
D
K
L
(
q
(
x
t
−
1
∣
x
t
,
x
0
)
∣
∣
p
θ
(
x
t
−
1
∣
x
t
)
)
]
E_{q(x_t|x_0)}\left[D_{KL}({q(x_{t-1}|x_t,x_0)}||p_\theta(x_{t-1}|x_t)) \right]
Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))]
就是要最小化上式中两个分布的KL散度,当然这两个分布的均值和方差都已经知道,可以套KL的计算公式:
D
K
L
(
N
(
x
;
μ
x
,
Σ
x
)
∣
∣
N
(
y
;
μ
y
,
Σ
y
)
)
=
1
2
[
log
∣
Σ
y
∣
∣
Σ
x
∣
−
d
+
t
r
(
Σ
y
−
1
Σ
x
)
+
(
μ
y
−
μ
x
)
T
Σ
y
−
1
(
μ
y
−
μ
x
)
]
D_{KL}(\mathcal{N}(x;\mu_x,\Sigma_x)||\mathcal{N}(y;\mu_y,\Sigma_y))=\cfrac{1}{2}\left[\log\cfrac{|\Sigma_y|}{|\Sigma_x|}-d+tr(\Sigma_y^{-1}\Sigma_x) +(\mu_y-\mu_x)^T\Sigma_y^{-1}(\mu_y-\mu_x)\right]
DKL(N(x;μx,Σx)∣∣N(y;μy,Σy))=21[log∣Σx∣∣Σy∣−d+tr(Σy−1Σx)+(μy−μx)TΣy−1(μy−μx)]
但是实际上不用这么复杂,看下图:
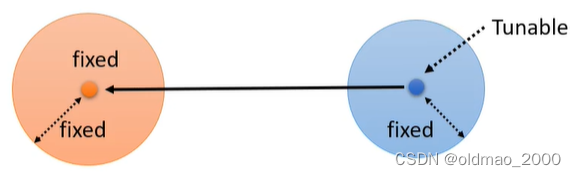
橙色分布是
q
(
x
t
−
1
∣
x
t
,
x
0
)
q(x_{t-1}|x_t,x_0)
q(xt−1∣xt,x0),上面的推导显示该分布的均值和方差都是固定值;蓝色分布是
p
θ
(
x
t
−
1
∣
x
t
)
p_\theta(x_{t-1}|x_t)
pθ(xt−1∣xt)它的方差是固定的,但是均值是变动的,要想使得两个分布接近,就是要将蓝色分布的均值想橙色均值移动。蓝色分布的均值是通过Denoise模块得来的:
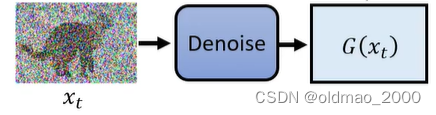
也就是要训练Denoise模块,使其得到分布的均值与橙色部分的均值越接近越好。
有了思路,下面来把denoising matching term
E
q
(
x
t
∣
x
0
)
[
D
K
L
(
q
(
x
t
−
1
∣
x
t
,
x
0
)
∣
∣
p
θ
(
x
t
−
1
∣
x
t
)
)
]
E_{q(x_t|x_0)}\left[D_{KL}({q(x_{t-1}|x_t,x_0)}||p_\theta(x_{t-1}|x_t)) \right]
Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))]
最小化思路写出来:
1.根据期望中的
q
(
x
t
∣
x
0
)
q(x_t|x_0)
q(xt∣x0)知道,
x
0
x_0
x0是已知的,因此,我们先从训练数据中先采样一张图片:

2.然后根据
x
0
x_0
x0计算(或者说采样)出
x
t
x_t
xt,过程可根据公式:
x
t
=
α
ˉ
t
x
0
+
1
−
α
ˉ
t
ϵ
x_t=\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon
xt=αˉtx0+1−αˉtϵ
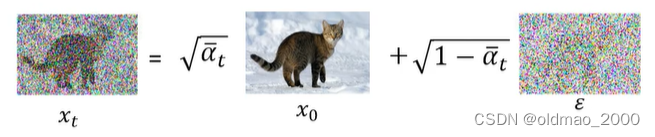
3.将
x
t
x_t
xt和
t
t
t丢进Denoise模块,期待模块输出的结果与橙色分布均值越接近越好:
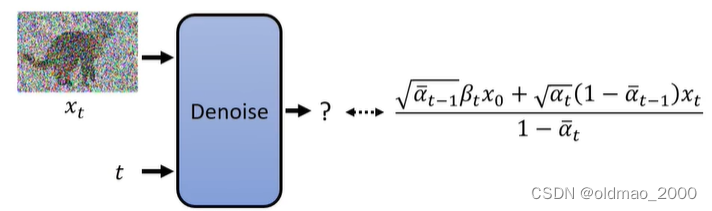
q
(
x
t
−
1
∣
x
t
,
x
0
)
q(x_{t-1}|x_t,x_0)
q(xt−1∣xt,x0)是橙色分布,是
x
t
−
1
x_{t-1}
xt−1的分布,但是可以从其均值公式中可以看到它与
x
t
−
1
x_{t-1}
xt−1没有关系,只是
x
0
x_0
x0和
x
t
x_t
xt的某种权重的结合结果。
将上式进行化简,把
x
0
x_0
x0替换一下,根据:
x
t
=
α
ˉ
t
x
0
+
1
−
α
ˉ
t
ϵ
x
t
−
1
−
α
ˉ
t
ϵ
=
α
ˉ
t
x
0
x
t
−
1
−
α
ˉ
t
ϵ
α
ˉ
t
=
x
0
x_t=\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon\\ x_t-\sqrt{1-\bar\alpha_t}\epsilon=\sqrt{\bar\alpha_t}x_0\\ \cfrac{x_t-\sqrt{1-\bar\alpha_t}\epsilon}{\sqrt{\bar\alpha_t}}=x_0
xt=αˉtx0+1−αˉtϵxt−1−αˉtϵ=αˉtx0αˉtxt−1−αˉtϵ=x0
则有:
α
t
(
1
−
α
ˉ
t
−
1
)
x
t
+
α
ˉ
t
−
1
β
t
x
0
1
−
α
ˉ
t
=
α
t
(
1
−
α
ˉ
t
−
1
)
x
t
+
α
ˉ
t
−
1
β
t
x
t
−
1
−
α
ˉ
t
ϵ
α
ˉ
t
1
−
α
ˉ
t
=
1
α
t
(
x
t
−
1
−
α
t
1
−
1
−
α
ˉ
t
ϵ
)
\cfrac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}\beta_tx_0}{1-\bar\alpha_t}\\ =\cfrac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t+\sqrt{\bar\alpha_{t-1}}\beta_t\cfrac{x_t-\sqrt{1-\bar\alpha_t}\epsilon}{\sqrt{\bar\alpha_t}}}{1-\bar\alpha_t}\\ =\cfrac{1}{\sqrt{\alpha_t}}\left(x_t-\cfrac{1-\alpha_t}{1-\sqrt{1-\bar\alpha_t}} \epsilon\right)
1−αˉtαt(1−αˉt−1)xt+αˉt−1βtx0=1−αˉtαt(1−αˉt−1)xt+αˉt−1βtαˉtxt−1−αˉtϵ=αt1(xt−1−1−αˉt1−αtϵ)
因此,Denoise模型最后要输出的东西如下图所示:
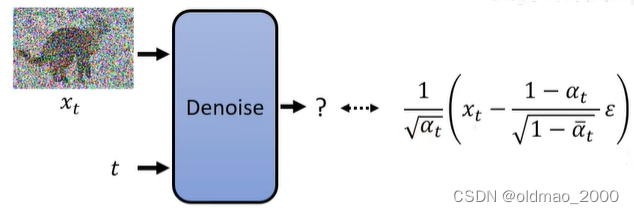
可以看到,Denoise模型只需要预测
ϵ
\epsilon
ϵ就可以,其他的
x
t
x_t
xt是已知量,
α
t
\alpha_t
αt是超参数1。
这个式子也是原文采样算法中的第四步的式子。

但是第四步中还有一项:
σ
t
z
\sigma_tz
σtz
这项是一个噪音,如下图所示,经过Denoise模块得到的是一个高斯分布的Mean,加上一个噪音后,相当于加上了一个Variance,也相当于对分布进行了因此采样。

σ t z \sigma_tz σtz的猜想
为什么要加这项噪音,而不直接使用分布的Mean?以下内容非原论文内容,而是老师自己的解读。
Mean是概率密度分布最大的值,使用概率最大的作为输出会有问题。
同样的现象在GPT里面也有:
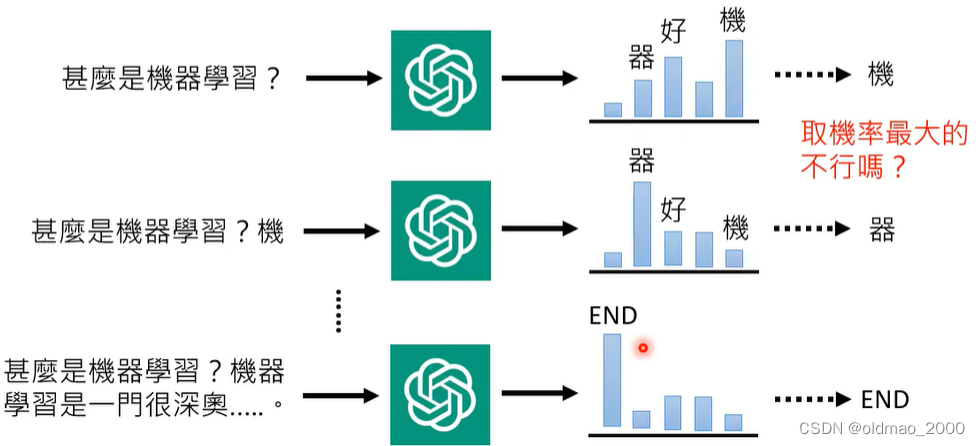
GPT中也是先产生一个概率分布,然后再从分布中进行采样,而不是取几率最大那个,这样做理论上可以带来一些随机性,使得模型在回答同一个问题的时候会给出不同的答案。但又为什么一定要有随机性,而非固定最大概率?
研究者在文章The Curious Case of Neural Text Degeneration中大概给出一些答案。

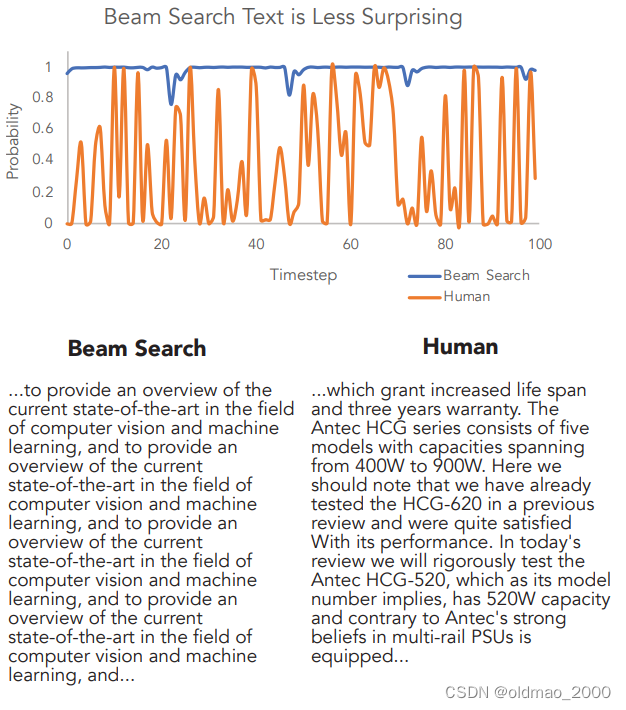
在给定上下文的情况下,只取概率最大的文字就会像蓝色文字一样,变成复读机,而加入采样的结果就比较正常(红字)。
同样,该文章还对比了取概率最大(蓝色线)以及人类(橙色线)的概率曲线,可以看到人类写作过程中用词经过GPT来算得到概率并不是选择最大那个。而蓝色线对应的文本又出现了复读机现象。
语音处理方面也有类似操作,Natural TTS Synthesis by Conditioning WaveNet on Mel Spectrogram Predictions的模型如下:
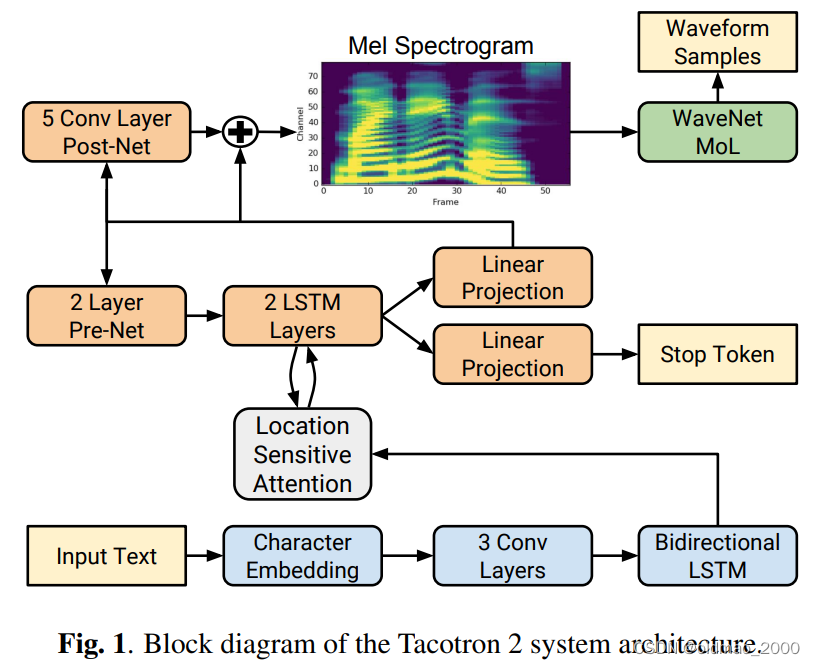
该文章在Decoder部分加了抓爆:
The convolutional layers in the network are regularized using dropout [25] with probability 0.5, and LSTM layers are regularized using zoneout [26] with probability 0.1. In order to introduce output variation at inference time, dropout with probability 0.5 is applied only to layers in the pre-net of the autoregressive decoder.
在做类似上面End2End的模型需要在inference的阶段加抓爆,会得到比较好的结果。
对于Diffusion Model来说,它可以看做是一种Autoregressive模型的特例,Autoregressive模型通常是一次到位,而Diffusion Model而是 分解为N次到位,每一小步的Denoise都可以看做是一次Autoregressive,既然Autoregressive中加随机性效果有提升,那么在Denoise过程加随机性效果也会有提升:
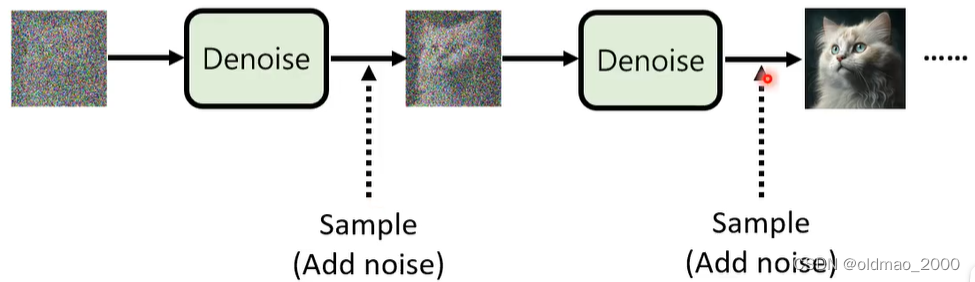
最后基于DDPM的原文代码,进行了是否加随机性的实验,结果如下:

Diffusion Model for Speech
Diffusion不但在图像上有应用,在语音方面效果也不错。谷歌团队的WaveGrad: Estimating Gradients for Waveform Generation中提出了WaveGrad。
WaveGrad原理和原始的Diffusion 模型很像,只不过noise变成了一维的而已。
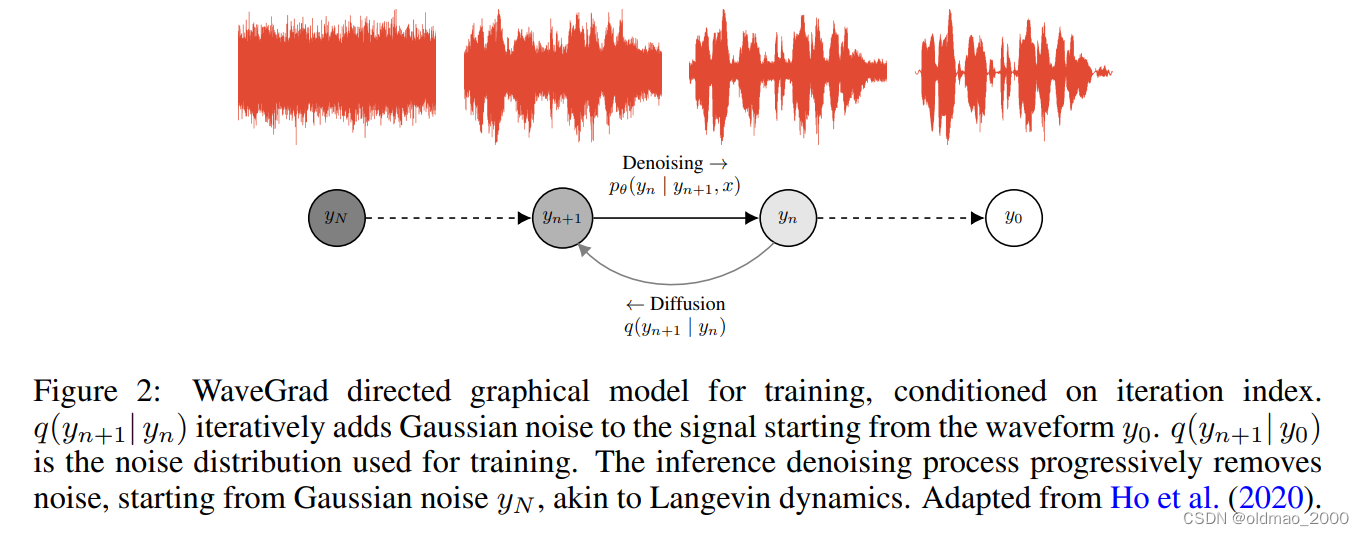
连算法都非常相似:

Diffusion Model for Text
文字直接用Diffusion Model是不行的,文字本身是Discrete的,难不成你要把文字变成乱码么,当然不行。

解决方法就是先将文字转换为Latent space中的向量表达,embedding是连续的,加noise没有问题。
斯坦福研究文章:Diffusion-LM Improves Controllable Text Generation
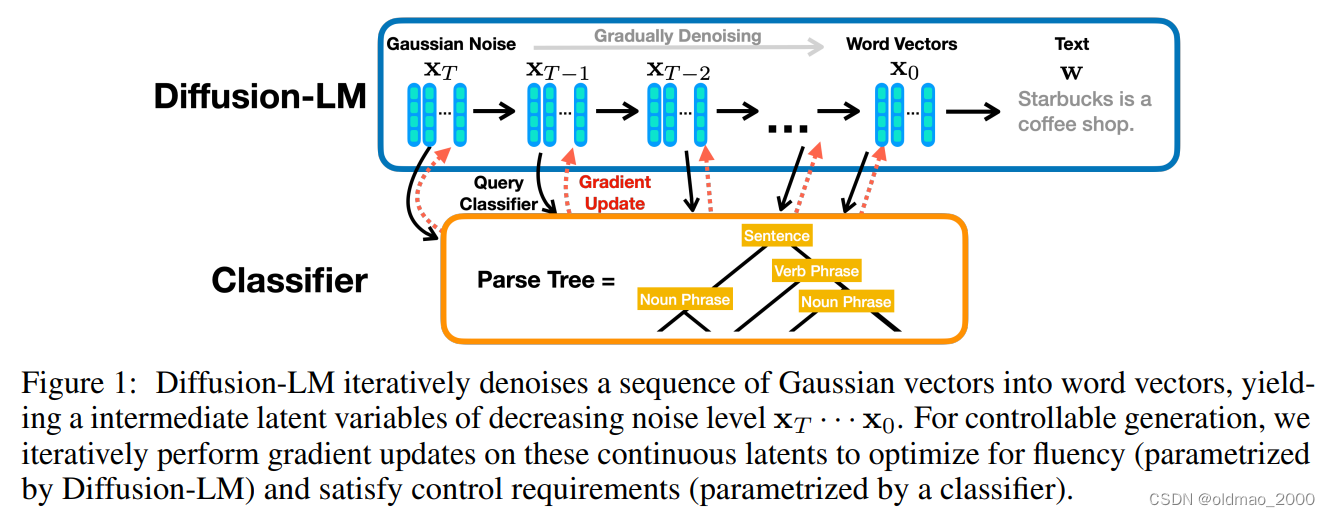
上海AI实验室团队发表在23年ICLR的DiffuSeq: Sequence to Sequence Text Generation with Diffusion Models也使用了相同的思路。
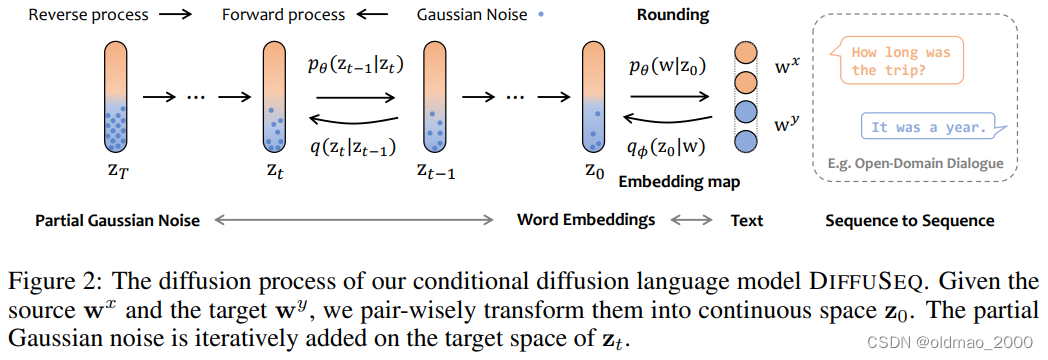
还有另外一种思路,既然文本不能直接加高斯分布的noise,可以尝试加其他形式的noise,在谷歌团队发表的DiffusER: Discrete Diffusion via Edit-based Reconstruction文章中,使用MASK标记作为noise:

模型构架如下:
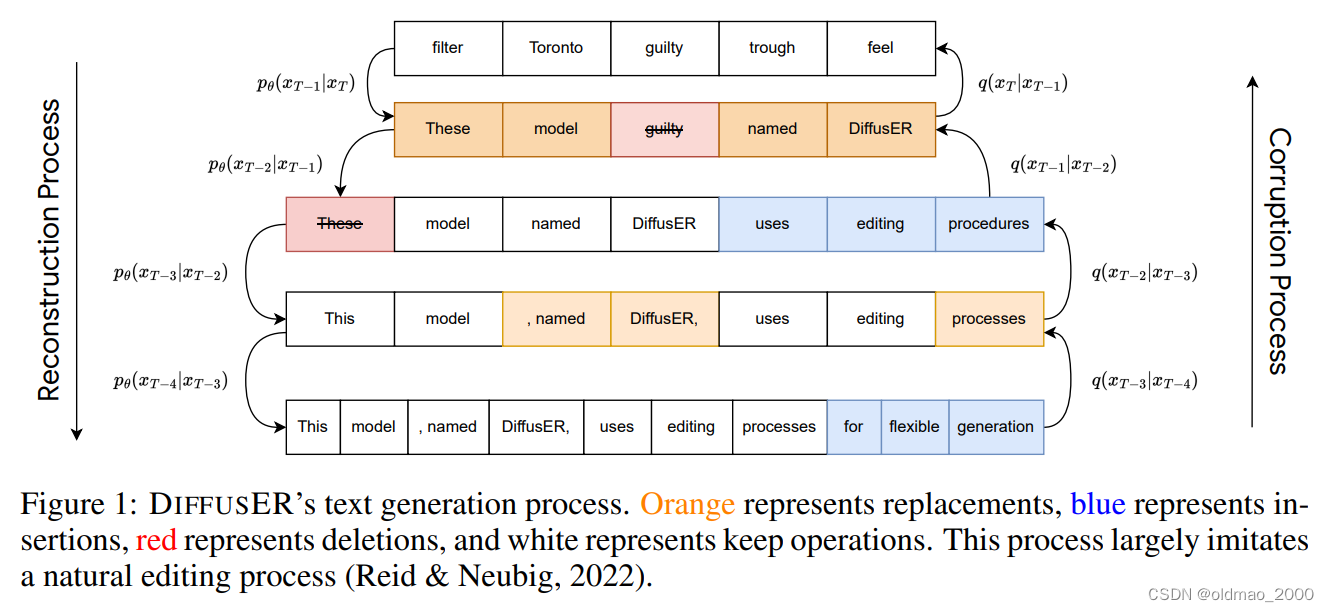
它是基于Edit操作的Diffusion模型,具体包括:
INSERT: The insertion operation is used to add new text to a sequence. For example in Figure 1, “uses editing processes” is added by DiffusER at timestep
x
T
−
2
x_{T−2}
xT−2.
DELETE: The deletion operation erases existing text. In Figure 1, this is shown when “These” gets deleted at timestep
x
T
−
2
→
x
T
−
3
x_{T−2} → x_{T−3}
xT−2→xT−3.
REPLACE: The replacement operation works overwriting existing text with new text. This is shown in Figure 1 at step
x
T
→
x
T
−
1
x_T → x_{T−1}
xT→xT−1 where “filter Toronto guilty trough feel” is replaced by “These model
guilty named DiffusER”.
KEEP: The keep operation ensures that a portion of the text remains unchanged into the next iteration. This is illustrated in timestep
x
T
−
2
→
x
T
−
3
x_{T−2} → x_{T−3}
xT−2→xT−3 where “model named DiffusER” is kept.
Mask-Predict
Diffusion模型的为什么效果很好?不是因为上面各种公式的推导,根本原因在于它结合各个击破和一次到位两种方式的优势(两种方式的解释可以看06.GPT-4+图像生成)
因为在Diffusion模型未出现之前就有研究将两种方式的优点进行了结合,思路就是将Non-Autoregressive模型改为Autoregressive模型,里面并未使用Diffusion中最大化似然的目标函数,但效果也很不错。
下面是脸书团队的文章成果:Mask-Predict: Parallel Decoding of Conditional Masked Language Models,假设有一个NLP的对话任务,该问句可以有两个答案,采用Non-Autoregressive模型(AutoEncoder,一次到位)可能会得到很差的模型,每个分布采样得到的结果合起来就是不知所云。
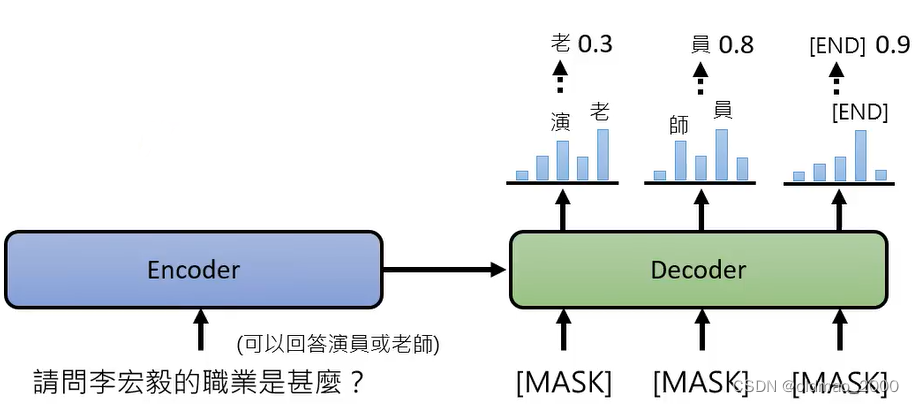
将上面的模型改成Autoregressive模型,把结果不好的结果(几率较低的部分)再次MASK,重新再做一次生成:
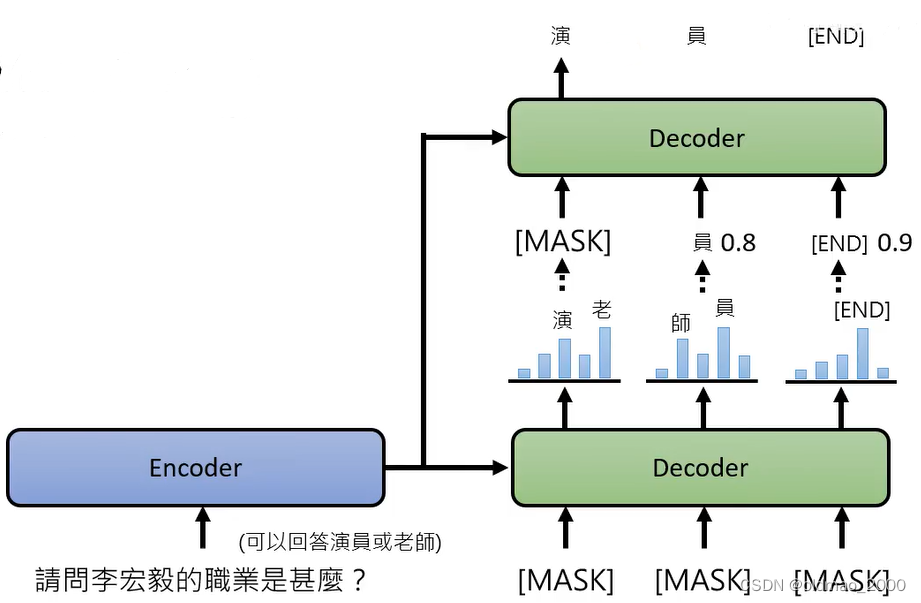
也就是在Decoder方向上做了Autoregressive
不光在NLP领域有这样是思路,在CV领域也有,称为:Masked Visual Token Modeling (MVTM),谷歌团队发表的文章有:
MaskGIT: Masked Generative Image Transformer
Muse: Text-To-Image Generation via Masked Generative Transformers
两篇文章一篇是单纯的图片生成,另外一篇是文字生成图片。
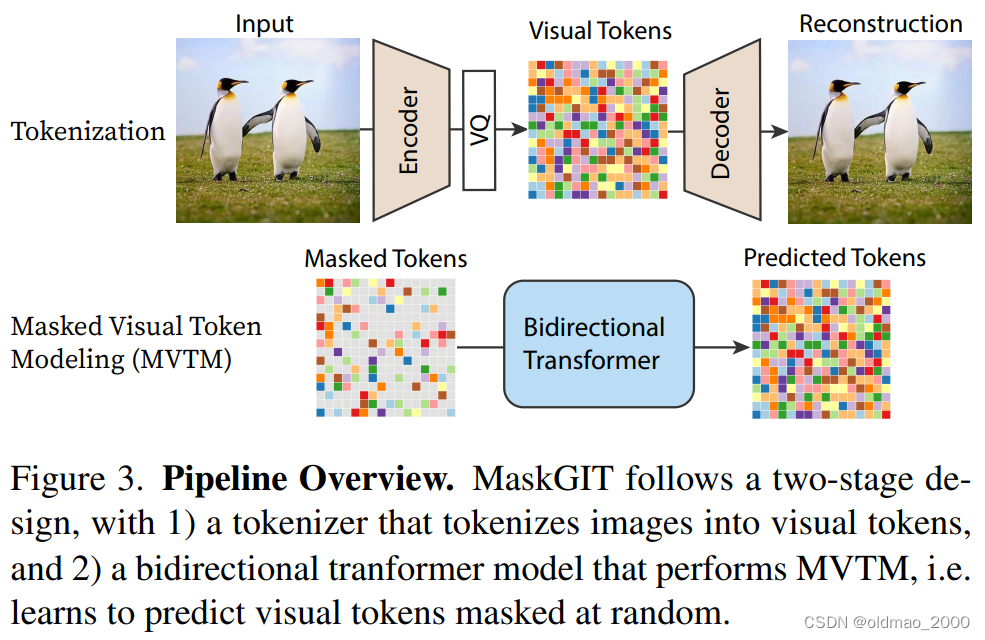
第一步先训练AutoEncoder,并获得图片的Visual Tokens,然后将Visual Tokens用灰色的Mask token随机盖住,然后训练一个bidirectional tranformer model将其还原为原来的Visual Tokens
在Inference阶段,丢一张全部都是mask的图片进Decoder,得到一个结果,然后将概率较低的部分再次mask,又丢进Decoder,直到图片生成完毕。

原文给出效果如下:

这里额外使用AutoEncoder中的Decoder做了图片可视化操作,该Decoder与还原mask的那个Decoder不是一个。
当然还对比了单纯一次一个pixel进行Autoregressive的结果:

可以看到,上面Non-Autoregressive仅仅使用了比较少的step就完成了图片生成,但是清晰度方面还是下面Autoregressive比较好。
问:为什么要把 α t \alpha_t αt做为超参数,而不去训练它?
答:DDPM作者有尝试过训练它,但是效果并没有明显提升;
α t \alpha_t αt其实是与 β \beta β递增序列有关,如何递增效果最好还未有定论,原文使用的是线性递增的关系,后来也有研究人员尝试使用别的递增关系尝试来提高DDPM的性能。 ↩︎