个人主页：兜里有颗棉花糖
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创
收录于专栏【手撕算法系列专栏】【AcWing算法提高学习专栏】
🍔本专栏旨在提高自己算法能力的同时，记录一下自己的学习过程，希望对大家有所帮助
🍓希望我们一起努力、成长，共同进步。

原题链接：点击直接跳转到该题目

一、AcWing 756. 蛇形矩阵

1️⃣题目描述

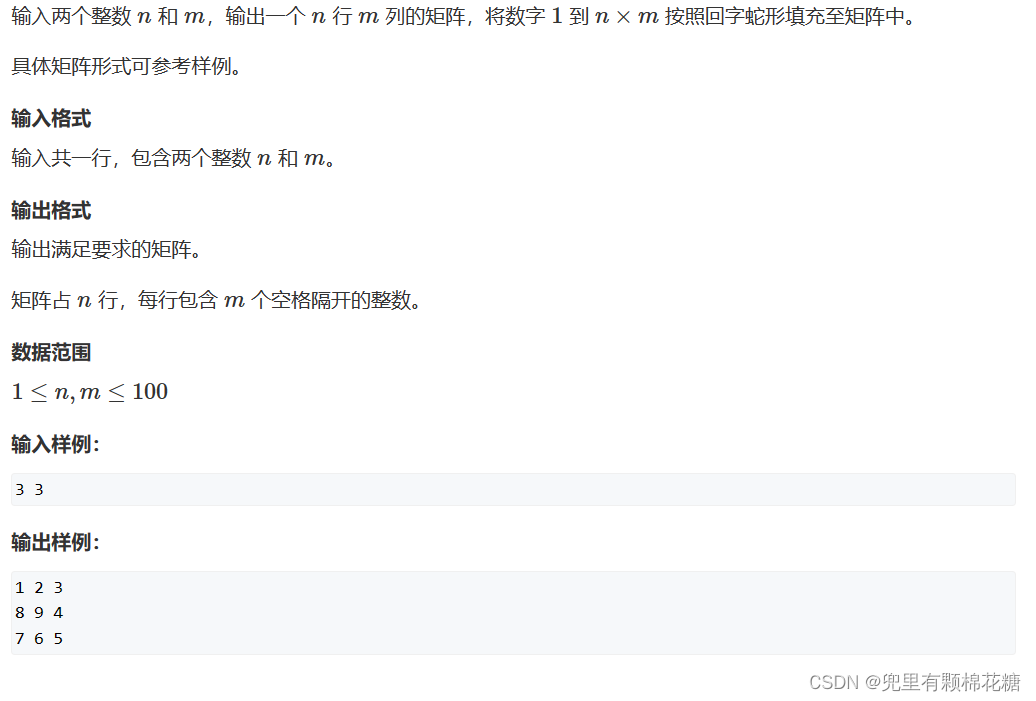
2️⃣题目解析

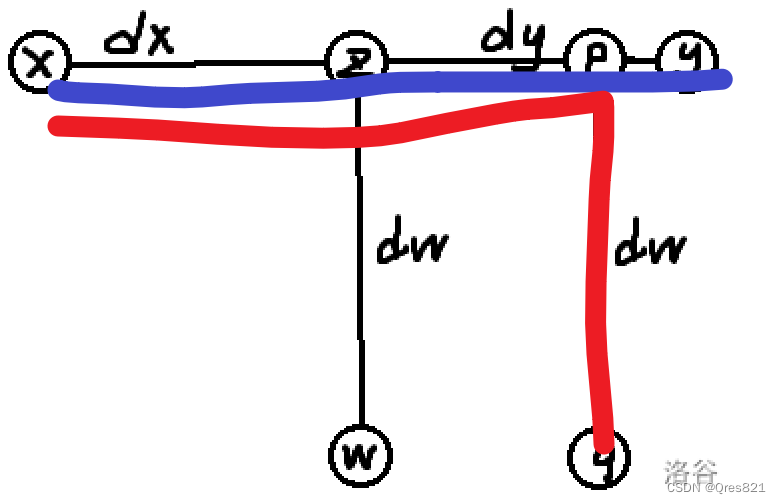
代码中：dx[] 和 dy[] 数组分别表示了在四个方向上 x 和 y 的变化量。 x 和 y 则是当前要填充的位置坐标， d 则代表方向，初始方向为右（即初始化d为1，代表一开始的时候初始方向为右方向）。

代码先在 x、y 坐标处填充了当前的值 i，然后根据当前方向判断下一个要填的位置坐标。如果下个要填的位置超出边界或者已经被填充过，需要改变方向。

当发生改变方向时，采用了 (d + 1) % 4 的形式来改变方向，其中 % 4 是为了保证方向不超出 4 个。

3️⃣解题代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

const int N = 110;
int arr[N][N];

using namespace std;

int main()
{
    int n,m;
    cin >> n >> m;
    
    int dx[] = {-1,0,1,0},dy[] = {0,1,0,-1};

    int x = 0,y = 0,d = 1; // 这里我们初始化方向为有方向
    // 总共有4个方向:分别为上下左右,上为0、右为1、下为2、左为3
    // 这里我们要先把一开始要填的位置，即x = 0，y = 0的位置先提前定义出来
    
    for(int i = 1;i <= n * m;i++)
    {
        arr[x][y] = i;
        int a = x + dx[d],b = y + dy[d];
        if(a < 0 || a >= n || b < 0 || b >= m || arr[a][b])
        {
            d = (d + 1) % 4;
            a = x + dx[d],b = y + dy[d];
        }
        x = a,y = b; // 这里的x、y即为下一个要填的位置
    }
    
    // 打印最终的矩阵即可
    for(int i = 0;i < n;i++)
    {
        for(int j = 0;j < m;j++)
         printf("%d ",arr[i][j]);
        cout << endl;
    }
    return 0;
}

最后代码就顺利通过啦！！！

二、AcWing 40. 顺时针打印矩阵

1️⃣题目描述

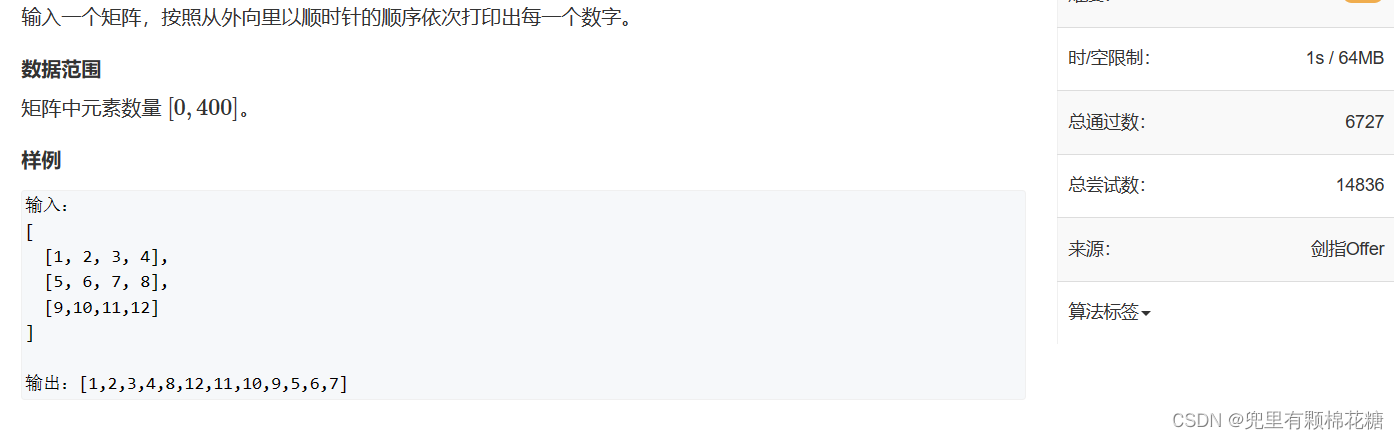
2️⃣解题代码

class Solution {
public:
    vector<int> printMatrix(vector<vector<int>>& matrix) {
        vector<int> res;
        if(matrix.empty()) return res;
        int n = matrix.size(),m = matrix[0].size();
        vector<vector<bool>> st(n,vector<bool>(m,false));
        int x = 0,y = 0,d = 1;
        int dx[] = {-1,0,1,0},dy[] = {0,1,0,-1};
        for(int i = 1;i <= n * m;i++)
        {
            res.push_back(matrix[x][y]);
            st[x][y] = true;
            int a = x + dx[d],b = y + dy[d];
            if(a < 0 || a >= n || b < 0 || b >= m || st[a][b])
            {
                d = (d + 1) % 4;
                a = x + dx[d],b = y + dy[d];
            }
            x = a,y = b;
        }
        return res;
    }
};

最后就是顺利通过啦！！！