目录
1. 什么叫汉诺塔
2. 分析算法原理
2.1. 当盘子的数量为1
2.2. 当盘子的数量为2
2.3. 当盘子的数量为3时
3. 编写代码
3.1. 挖掘重复子问题
3.2. 只关心某一个子问题如何处理
3.3. 递归的结束条件
3.4. 代码的编写
4. 递归展开图分析
1. 什么叫汉诺塔
力扣上的原题链接如下:
面试题 08.06. 汉诺塔问题 - 力扣(LeetCode)
什么叫汉诺塔呢?
汉诺塔是一种经典的数学智力游戏,它起源于印度。游戏中有三个竖立的柱子,通常称为"A"、“B”、“C”。最初,所有的圆盘按照从大到小的顺序叠放在"A"柱子上,最大的圆盘在底部,最小的圆盘在顶部。游戏的目标是将所有的圆盘从"A"柱子移动到"C"柱子上,但在移动过程中要遵守以下规则:
- 一次只能移动一个圆盘;
- 每次移动必须将一个圆盘从柱子的顶部移到另一个柱子的顶部;
- 移动过程中,大圆盘不能放在小圆盘的上面。
通过按照规则逐个移动圆盘,最后把所有圆盘都移动到"C"柱子上就完成了游戏。汉诺塔问题被广泛用作数学问题和编程算法的练习。它展示了递归算法的应用,因为解决汉诺塔问题的常用方法就是利用递归。
2. 分析算法原理
2.1. 当盘子的数量为1
初始情况如下:
此时只需要将A柱子的盘子直接移动到C柱子上即可。
2.2. 当盘子的数量为2
初始情况如下:
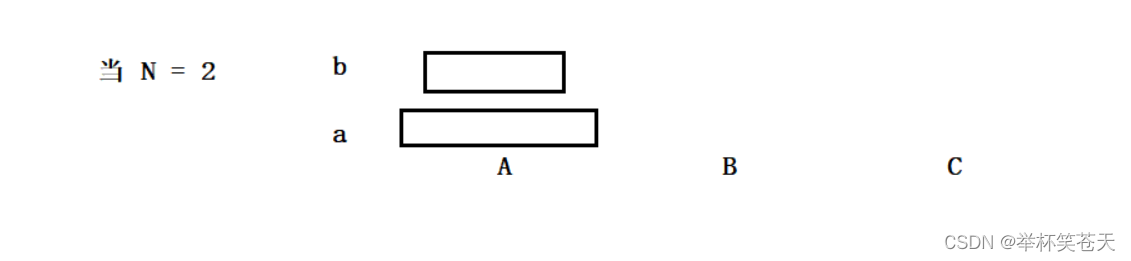
我们的目的是,将这两个盘子从A柱子移动到C住柱子。而要想将a盘子移动到C柱子上,那么首先要将b移动到B柱子上。
此时我们可以分为三个过程:
step 1:将b盘子以C柱子为辅助,移动到B柱子。
step 2:将a盘子直接移动到C柱子。
step 3:将b盘子以A柱子为辅助,移动到C柱子。
step 1:
将b盘子以C柱子为辅助,移动到B柱子

step 2:
将a盘子直接移动到C柱子

step 3:
将b盘子以A柱子为辅助,移动到C柱子
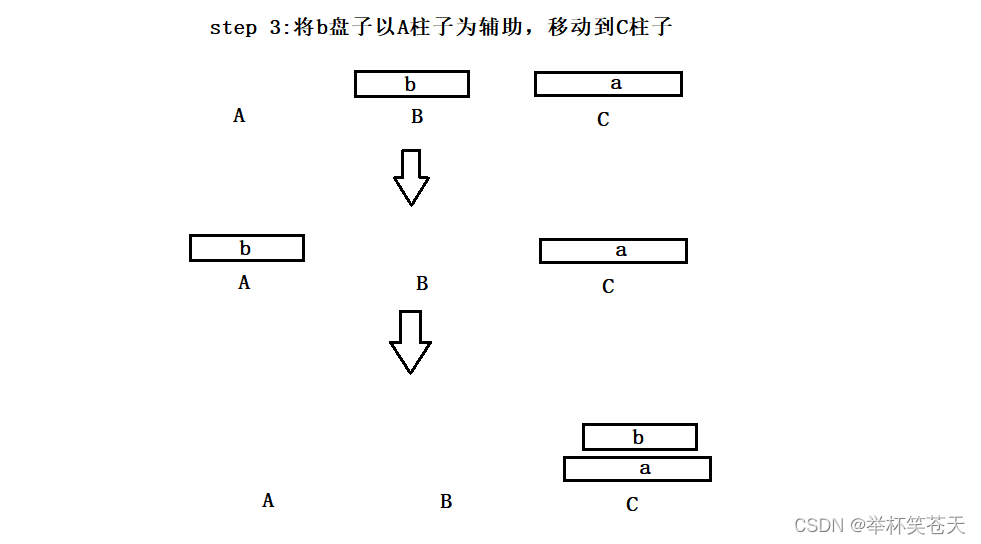
此时经过上面的三个过程就达到了我们的目的。
2.3. 当盘子的数量为3时

我们的目的是,将这三个盘子从A柱子移动到C住柱子。而要想将a盘子移动到C柱子上,那么首先要将a上面的柱子(把b和c看作为一个整体)移动到B柱子上。此时将b和c移动到B柱子上不就是当盘子数量为2吗,因此此时我们依旧可以分为三个过程:
step 1:将b和c盘子以C柱子为辅助,移动到B柱子。
step 2:将a盘子直接移动到C柱子。
step 3:将b和c盘子以A柱子为辅助,移动到C柱子。
step 1:将b和c盘子以C柱子为辅助,移动到B柱子

step 2: 将a盘子直接移动到C柱子。
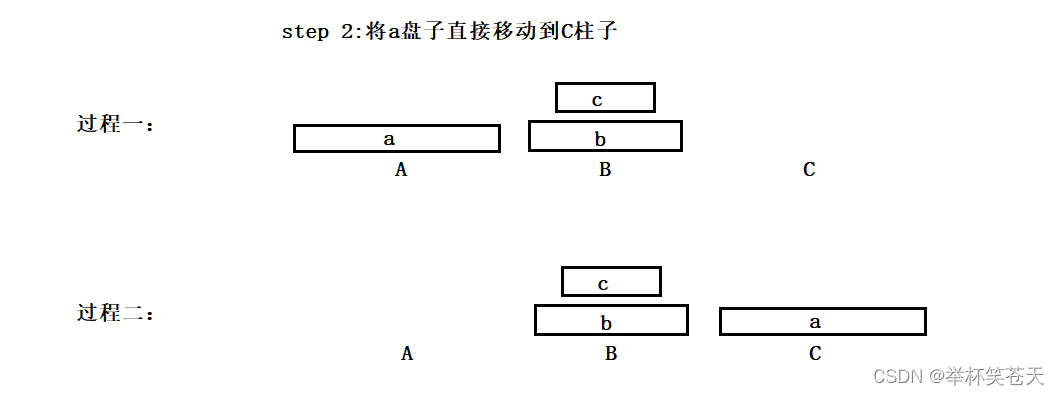
step 3: 将b和c盘子以A柱子为辅助,移动到C柱子

以此类推,我们发现,对于一个大问题,是可以被分为若干个相同类型的子问题,而这就是能用递归的原因。
那么我们的总结就是:
递归结束条件: 当盘子的数量 == 1时,直接处理;
递归中间过程: 当盘子的数量 >= 2时,我们分三个步骤处理;
我们将最下面的盘子称之为 Last; Last上面的所有盘子称之为 All
step 1: 将A柱子 "Last" 的 "All" 借助C柱子 移动到 B柱子。
step 2: 将A柱子 "Last" 直接移动到 C柱子上。
step 3: 将B柱子 "ALL" 借助 A柱子 移动到 C柱子上。
3. 编写代码
既然可以用递归处理,那么如何编写递归代码呢?我们可以分为三个步骤。
3.1. 挖掘重复子问题
这个步骤决定了递归的函数头,将问题抽象为函数头
汉诺塔的重复子问题:
将A柱子上的一堆盘子,以B柱子为辅助,移动到C柱子。
// 函数头如下:
// A、B、C 分别代表三个柱子
// n代表你要将几个盘子从A柱子,以B盘子为辅助,移动到C柱子
void _hanota(A,B,C,n);3.2. 只关心某一个子问题如何处理
这个步骤决定了递归的函数体。这一步只需要关注某一个子问题如何处理的,经过我们的分析算法原理,我们得知了任何一个子问题可以被分为三个过程,如下:
我们将最下面的盘子称之为 Last; Last上面的所有盘子称之为 All
step 1: 将A柱子 "Last" 的 "All" 借助C柱子 移动到 B柱子。
step 2: 将A柱子 "Last" 直接移动到 C柱子上。
step 3: 将B柱子的 "ALL" 借助 A柱子 移动到 C柱子上。
//step 1: 将A柱子 "Last" 的 "All" 借助C柱子 移动到 B柱子。
void _hanota(A,C,B,n-1);
//step 2: 将A柱子 "Last" 直接移动到 C柱子上。
A.back() ---> C
//step 3: 将B柱子上的 "ALL" 借助 A柱子 移动到 C柱子上。
void _hanota(B,A,C,n-1);3.3. 递归的结束条件
这个步骤决定了递归的出口,如何判定呢? 当一个问题不可以在被分为相同类型的子问题时,此时就是递归的结束条件。
经过我们前面的分析,当盘子的数量 == 1时,直接处理,此时就是递归的结束条件。
if(n == 1)
return ;3.4. 代码的编写
有了上面的分析,代码就非常简单了:
class Solution {
public:
void _hanota(vector<int>& A, vector<int>& B, vector<int>& C,size_t n)
{
// 递归出口
if(n == 1)
{
C.push_back(A.back());
A.pop_back();
return ;
}
// step 1:
_hanota(A,C,B,n-1);
// step 2:
C.push_back(A.back());
A.pop_back();
// step 3:
_hanota(B,A,C,n-1);
}
void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
_hanota(A,B,C,A.size());
}
};4. 递归展开图分析
为了更好地理解上面的代码,我们试画一下当N == 3时的递归展开图。同样,为了更好地画递归图,我们将递归出口的逻辑以 ’#‘ 表示,step 1、step 2、step 3、 分别以 (1)、(2)、(3)表示。

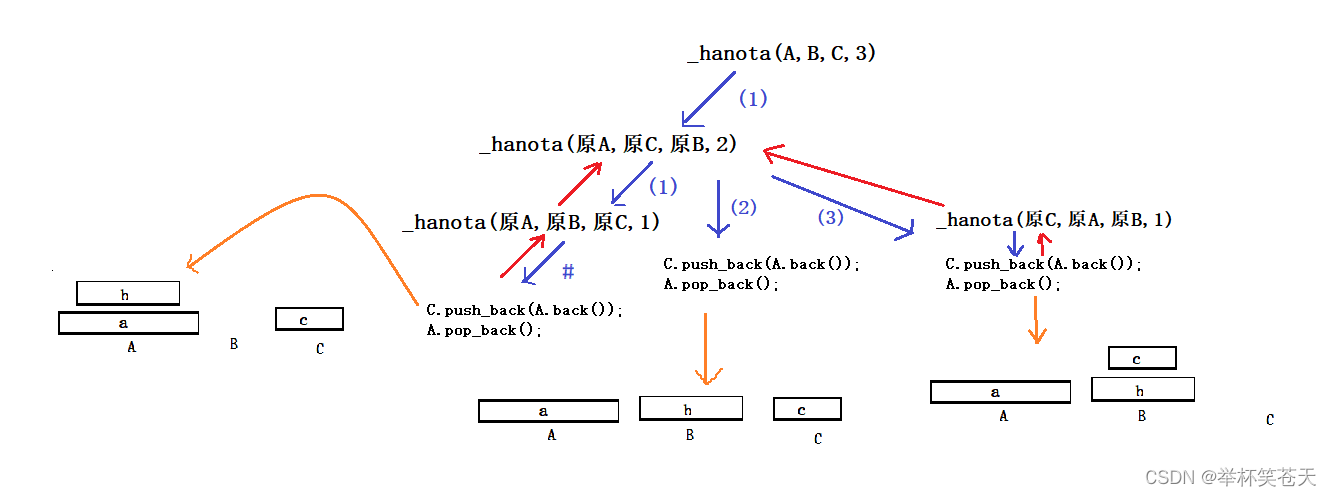
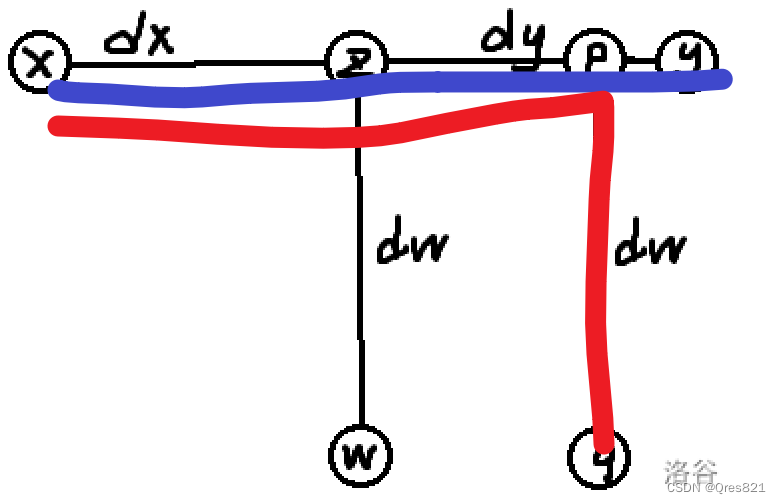
经过我们上面的函数的左边的递归展开图,我们应该可以了解它的过程了,当我们以宏观角度看,认为把A柱子上的b和c这两个盘子经由C柱子辅助移动到B柱子,是一个步骤;但是递归展开后,我们发现,每次当函数的盘子数量1时,才会移动盘子(而且移动的最上面的盘子)。所以我们的代码中移动的是A.back(),最后一个元素,而不是A[0]。
至此,我们的汉诺塔就此结束。