Hi, 你好。我是茶桁。

我们终于又开启新的篇章了，从今天这节课开始，我们会花几节课来理解一下深度学习的相关知识，了解神经网络，多层神经网络相关知识。并且，我们会尝试着来打造一个自己的深度学习框架。

以前很多时候都会被人问到很多问题，其中比较多的就包括现在各种各样的框架应该用到哪一个，在学习人工智能的时候，对于深度学习框架有比较多的问题。那在这里我就希望能帮助各位小伙伴彻底的去理解一下什么是学习框架。

对于我们来说，就像小孩子去学一个东西，最好的就是从头到尾能把它拆了，然后再重建起来。

从今天开始往后的几节课里，我们都会去好好了解「如何从零构建一个深度学习框架」。

本文目标

我们基本的核心目的就是来讲明白，什么是神经网络，以及神经网络的原理是什么。

我们要知道，人工智能有很多方法，但是神经网络是现代人工智能里面一个非常核心的内容。

咱们现在就是要先去了解神经网络的原理是怎么回事，然后在这个过程中我们来讲解清楚神经网络的框架到底是什么样的。

如我们之前学习过的几节机器学习课程，会发现它有很多的概念。

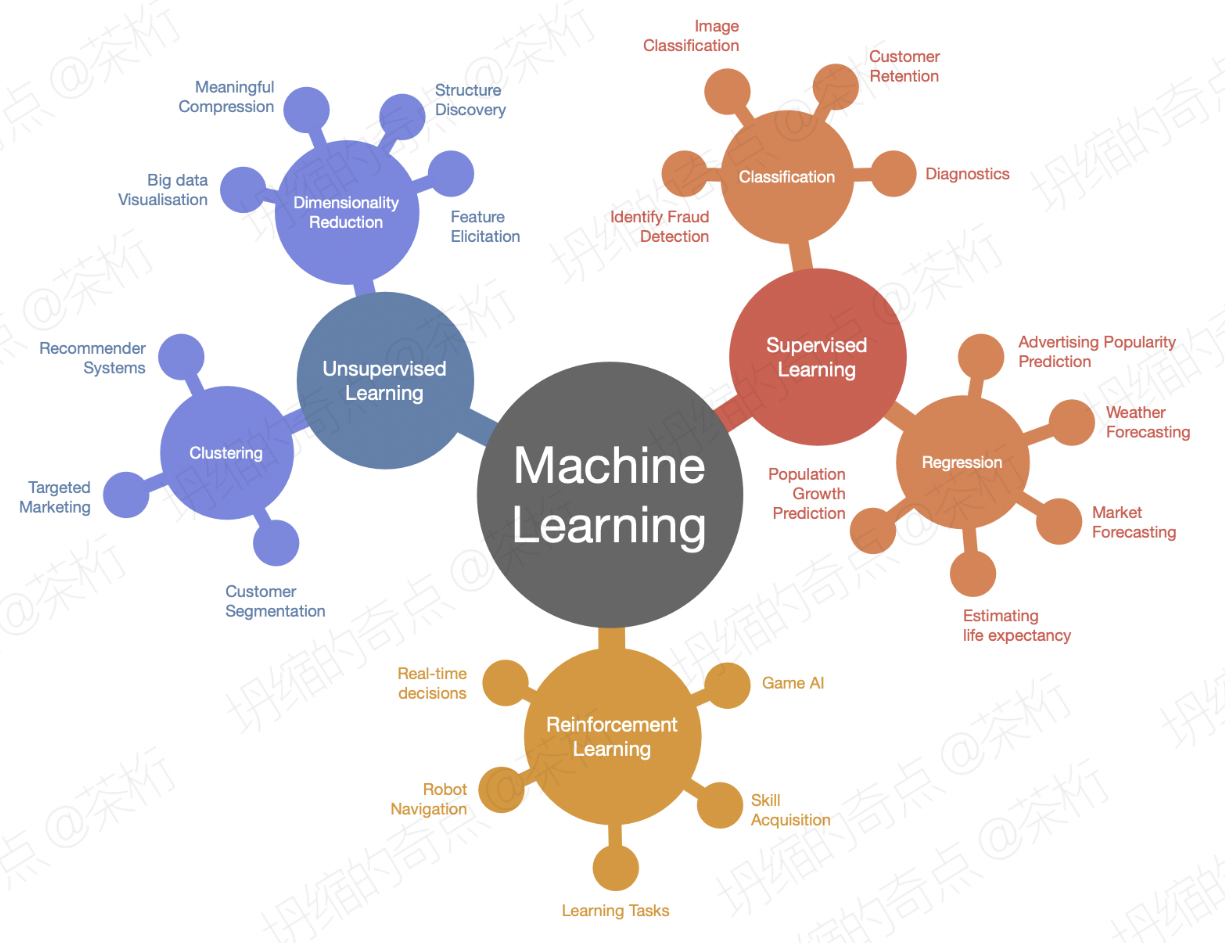
比方说非监督学习、监督学习、强化学习，监督学习里面又分了回归和分类等等。

很多人看到这些，在初次接触、初次学习的时候就觉得人工智能很复杂，很难学会。除此之外，我们在学到人工智能目前比较核心的一个内容是关于深度学习神经网络。好多人不知道深度学习神经网络到底是什么原理。

在整个学习过程会发现有很多很多的问题，概念很多，变体也很多，学习很困难。

那这里要跟大家强调一点，就是千万别成为「马保国」，为什么这里会提到这个人呢？在我看来，这其实是一类人，他是一类人的代表。就是整很多的概念，假装子集很厉害。

就是我们脑子里不要总是去提很多概念，或者说很多很花哨的东西，最重要的还是基本功修炼好。我一直都强调一个观念，就是基础学科，基本功才是所有学科的基石。过多的概念其实并没有什么卵用。

早些时候，我上班的地方有一个叫「李雨晨」（匿名🙄）的产品经理，各种概念信手拈来，都是一些高大上的东西。也是将面试官唬的一愣一愣的。当时大家也是没多想，心想人家既然是个牛逼人物，那就多配合人家呗，结果是没过3个月就原形毕露，当然是下面干事的人最先觉察出来的。

没办法，为了继续装下去只能是利用自己的职权和谎言去盗用别人的成果，比如设计稿啊，文档啊啥的，拿着当自己的东西向上汇报。

再然后，基本人人都开始防着他了，就开始恼羞成怒，一直打压那个最开始说他不行并防着他的产品。不过不行就是不行，其实最开始就能看出端倪，因为基本没有一家公司干活超过6个月，那肯定是有问题的。就这资质也能忽悠成高级产品经理，也能看出来那会儿产品这个行业的水份多大，门槛多低。不过终归潮水退了之后，裸泳的王八都要现行是吧。

好，说这么多吐槽的话其实也是想说一个道理，不要去搞花里胡哨的玩意，踏踏实实的把基本功练扎实，否则一时唬的了人，但是终归是走不远。

那这也是咱们这节课的目的，让大家去除掉背后这些繁杂的表象，那么它背后到底是什么，这就是咱们这三天的目的。

这些年，人工智能已经应用到我们各个地方了。先不说现在大火的AIGC，人工智能还应用到其他各个地方。

比方说在商场购物的时候，它的楼宇灯光，自动停车都是在做这些事情。买票的时候，机场，火车站都有人脸识别。每天给你推荐的各种商品，以及我们做物流配送等等这些东西，背后都有人工智能。

而这些人工智能背后有一个很重要的东西，就是用到了神经网络框架。

比方说众所周知的TensorFlow, 我们每次调用的时候，框架背后调用了很多东西。

# Store layers weight & bias
# A random value generator to initialize weights.
random_normal = tf.initializers.RandomNormal()

weights = {
    'h1': tf.Variable(random_normal([num_features, n_hidden_1])),
    'h2': tf.Variable(random_normal([n_hidden_1, n_hidden_2])),
    'out': tf.Variable(random_normal([n_hidden_2, num_classes]))
}

biases = {
    'b1': tf.Variable(tf.zeros([n_hidden_1])),
    'b2': tf.Variable(tf.zeros([n_hidden_2])),
    'out': tf.Variable(tf.zeros([num_classes]))
}
...

# Create model.
def neural_net(x):
    # Hidden fully connected layer with 128 neurons.
    layer_1 = tf.add(tf.matmul(x, weights['h1']), biases['b1'])
    # Apply sigmoid to layer_1 output for non_linerity.
    layer_1 = tf.nn.sigmoid(layer_1)

    # Hidden fully connected layer with 256 neurons.
    layer_2 = tf.add(tf.matmul(layer_1, weights['h2']), biases['b2'])
    # Apply sigmoid to layer_1 output for non_linerity.
    layer_2 = tf.nn.sigmoid(layer_2)

    # Output fully connected layer with a neuron for each class.
    out_layer = tf.matmul(layer_2, weights['out']) + biases['out']
    # Apply softmax to normalize the logits to a probability distribution
    return tf.nn.softmax(out_layer)

我们现在想把这些框架搞清楚，就需要知道它背后这些东西到底是什么原理、什么原因。

那这几节课之后，就希望我们能从0到1学会创建一个深度学习框架，从底层来理解这个神经网络的原理，理解现代人工智能的核心。

一开始的课程，内容也会稍微比较简单一些，越往后咱们就越难一点。最后，彻底理解深度学习神经网络原理。

预测趋势与关系

我们以一个趋势预测的问题为引入。

如果对于自然哲学或者说科学研究这些，就是对科学研究方法论感兴趣的话，你会知道我们整个科学研究其实分为三个层面。

不管是牛顿、爱因斯坦，还是伽利略、图灵等等，所有的科学研究，所有的research，不管是关于数据还是别的，它都是三个层面。

第一个层面叫做描述性的，第二个叫做因果推理，第三个叫做未来的预测。

就说我们所有的科学活动，所有的研究活动都可以归为这三类。

描述性的东西，比方说你又长胖了多少，然后又增加了多少重量。今天的体重，明天的体重等等。

除此之外第二个层面是我们要看出来它们之间的相关性。比方吃的多和你长胖，它们之间是呈正相关的。还有其他的一些关系，比方说是呈负相关的等等。

那我们最重要也是最难的一个科学活动是要对它进行未来的预测，对于未来的预测。这个未来它不仅是predict。

比方说现在你知道的是几组数据，知道每个对应的结果。然后你看到了一组没有见过的数据，你去预测它。

就好比一个孩子做题，他见过的题都能做，没见过的题他也要会做。这个其实就是属于对未来的一种预测能力。

关于预测，我们最关心的预测是关于我们的身体健康，能活多久；还有就是关于挣钱的问题。

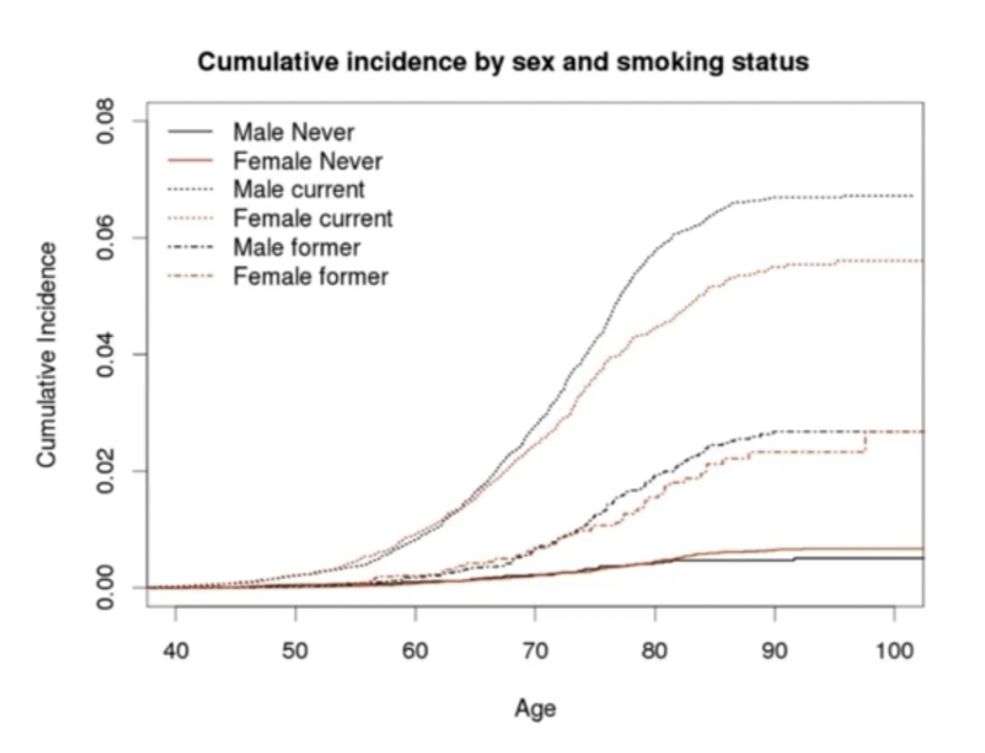
我们看一下这个例子，你的性别和你的吸烟的频率，跟一种疾病（可能是肺癌），它会有一个相对应的概率。

性别不同，年龄不同，抽烟频率不同。我们会发现，得病概率随着年龄的增大并不会有多少增加，此时男性得病概率反而比女性还小。

但是随着抽烟频率越多，得病概率上升的非常快。其中呢，同样的年龄和抽烟频率下，男性得病的概率则会更高。

假设存在一个人p，男性，年龄是72岁，他每天抽三根：P{age:72, sex: male, rate: 3/day}。那他得这种病的概率大约是多少？那我们就先在图上随意画一个，假如说就如图的位置一样的概率：

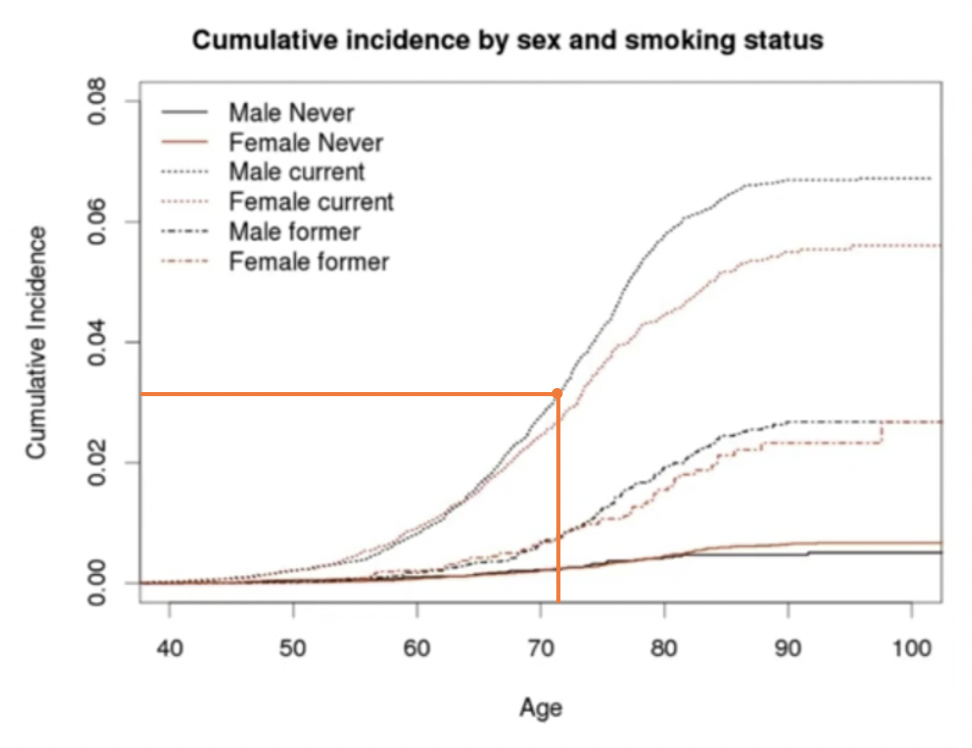
那么这个概率到底是多少？我们就需要用到数据去做预测，此时我们就得去做个拟合。

除此之外，我们再来看BMI，也就是身体指数。身体指数就是体重除以身高的平方：BMI = kg/h^2，越大就表示你越胖。

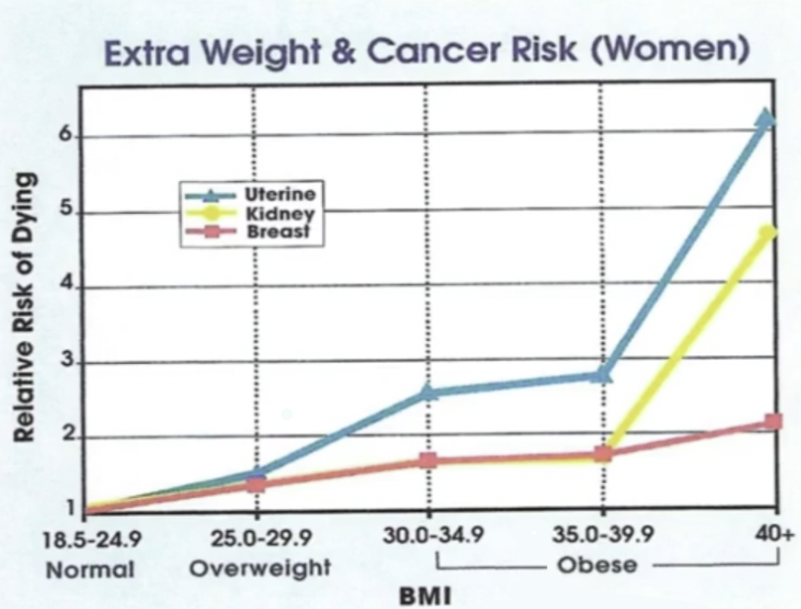
当你到某一个值的时候，可以看到得病的概率。

我们假设有一个人180斤，身高一米73，我们来预测他得肾病的概率是多少。这个时候我们还是需要去做预测。

波士顿房价预测

现在就来看一个非常经典的预测案例：波士顿房价案例。这个波士顿房价的数据，我们曾经在机器学习的线性回归里有用到，不知道小伙伴们有没有去看过。

波士顿地区是在美国东北部，房地产的价钱也比较稳定，那这个数据也是比较老的数据了，通过这些数据来考察，希望机器能够根据输入的内容来预测它的房价。

现在就以波士顿房价问题为例，来讲讲计算机怎么去预测。然后在预测的过程中我们来讲解实现深度学习的原理。最终把它封装成我们所需要的一个深度学习框架。

第一步自然是加载和分析数据。

之前的课程我提到过，这个数据由于一些原因，sklearn的datasets中已经删除了，那我们要想加载数据，就需要用到其中的fetch_openml：

from sklearn.datasets import fetch_openml

dataset = fetch_openml(name='boston', version=1, as_frame=True, return_X_y=False, parser='pandas')

在我们第一次获取到这个数据不知道怎么处理的时候，我们可以使用dir来看看这个数据里面的内容：

dir(dataset)

---
['DESCR', 'categories', 'data', 'details', 'feature_names', 'frame', 'target', 'target_names', 'url']

我们看到这个dataset里有一个feature_names，直觉上这个应该是一些特征名称，我们来查看一下这个的内容：

dataset['feature_names']

---
['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']

这里要说明一下，因为我是用的Jupyter，所以我可以这样直接打印出变量的具体内容，如果小伙伴们不是在Jupyter里，而是在Python文件中去编写代码，不要忘了使用print函数。

在拿到数据之后，我们先来定义一下问题。 就是假设你现在要买一个房子，那么你就要根据他的这个房子的相关数据，来判断这个房子到底应该能卖到多少钱。所以我们的任务就是给定一组房屋的数据，然后要能够预测售价是多少。

定义完问题之后，我们来分析一下数据。

首先，要做数据,我们会先把它装载到一个表格里边。这里，我们使用Pandas。

Pandas在Python基础课里我有详细的讲过，它是做数据科学非常常用的一个东西。不要把它认为是熊猫啊，它是panel data set的缩写，就是「面板数据集」，可以理解为一个Excel。可是它比Excel更方便编程。

import pandas as pd
data = dataset['data']
dataframe = pd.DataFrame(data)
print(len(dataframe))
dataframe.head(5)

为了节省篇幅，打印结果我就不贴出来了。

有的小伙伴在处理这里data的时候，会发现头部没有特征名，会呈现1， 2， 3， 4这样的数字。我们就需要将名称给它加上，之前我们说过，feature_name是特征名，于是：

dataframe.columns = dataset['feature_names]

这个时候我们就能看出来每一个特征到底是什么。不过这组数据里因为只是特征数据，并没有相关的价格。价格原本是目标数据，也就是最初始数据里的target，所以我们这里给这组特征数据里加上一列。

dataframe['price'] = dataset['target']

然后我们要想看看到底什么因素对房价的影响是最大的。「What’s the most significant（salient） feature of the house price」。

对于决定一个东西最重要的特征我们就叫做significant，或者silence，显著特征。

在pandas里边有一个很简单的东西，correlation。correlation就是两组变量的相关性。

关于特征相关性，我们在机器学习里面有详细的讲过，这里我们就粗略带过就行了，在使用corr()找到特征之间的相关性数据之后，可以使用seaborn来将热图可视化出来：

import seaborn as sns

sns.heatmap(dataframe.corr())

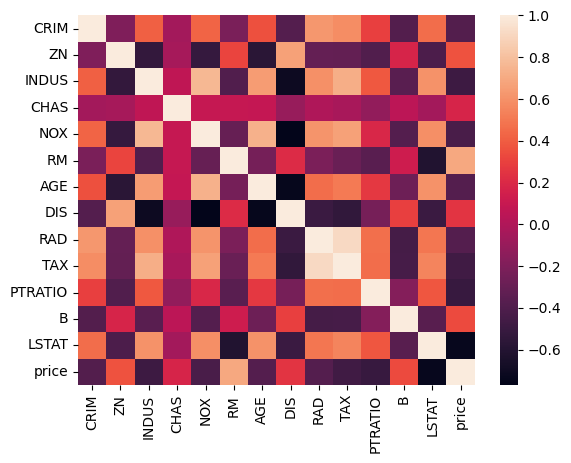
这里我们着重来看和价格相关的特征，除了它本身之外，正相关性最大的就是RM，负相关性最大的是LSTAT。

我们来看一下这两个特征的说明：

print(dataset['DESCR'])

---
...
RM       average number of rooms per dwelling
LSTAT    % lower status of the population
...

RM是一套住宅的房间数量，一个是低收入人群的人口比例。也就是说，房间越多的房子越贵，小区内低收入人群的比例越低，小区内的房子越贵。那小区内低收入人群的比例居然比犯罪率的影响还要大一些，似乎有点让人难以接受，但是这个确实是事实。

基于以上分析，我们需要把房屋里边卧室的个数和房屋价格最成正相关。

把问题简单化：如何依据房屋里边卧室的数量来估计房子的面积?

在一九七几年的时候啊, 当时有过这样一种想法，首先，我们将所有的RM数据存下来, 还有目标数据，也就是price也存下来：

X_rm = dataframe['RM'].values
y = dataframe['price']

存下来之后我们把做一个字典映射：

rm_to_price = {r: y for r, y in zip(X_rm, y)}

---
{6.575: 24.0,
 6.421: 21.6,
 ...
 6.976: 23.9}

这样之后，问题也就相应的做了一个简化。假如有人在销售那里要求买房子，那销售就可以拿出一个字典，里面都是这样的对应关系，然后我们就可以去查一下就知道了。

这个时候假如有人告诉你有一个小区，他平均里边房屋平均是6.421。那一查就发现这个6.421的基本上卖21万。那如果小区里房屋数量是5.57的时候我卖多少钱？卖13万。这都是一一对应的关系。

rm_to_price[6.421]

---
21.6

不过这个时候有一个人说我们那个小区里面平均是7个房间，那是多少呢？我们发现，我们的字典里没有超过7的数字，也就是没有这么一个对应关系。

那么找不到的时候怎么办呢？我们大部分时候解决问题都会找一个近似值，也就是最接近的数据来做参考。也可以根据以前的数据来做计算， 其实也就是一句话的事：

def find_price_by_simila(history_price, query_x, topn=3):
    return np.mean([p for x, p in sorted(history_price.items(), key=lambda x_y: (x_y[0] - query_x) **2)[:topn]])

要根据以前的数据来做计算的话，我们定义了一个方法，传入了参数历史价格以及查询特征。然后我们返回的内容稍微有点复杂，首先给这个房屋进行排序，排序依据是按照x和query之间的距离来给他排序。排序的时候我们取最接近的这几个数字，这样就能够得到最接近的x和y。然后在x和y里面我们取它的price，这就是最接近的price。

然后我们来看看它给咱们算的如果房间数是7的情况是什么价格：

find_price_by_simila(rm_to_price, 7)

---
29.233333333333334

关于排序那里看不懂的小伙伴，我们这里额外花点篇幅开个小灶。这样，假如说我们有下面一组数据：

person_and_age = {
    'A张学友': 62,
    'C周杰伦': 44,
    'B毛不易': 29
}

然后我们将这组数据改成列表并进行排序：

l = list(person_and_age.items())
sorted(l)

---
[('A张学友', 62), ('B毛不易', 29), ('C周杰伦', 44)]

我们可以看到它是按照数据的首字母进行排序的，可是这个时候我们不想以首字母来排序，而是想根据年龄大小进行排序该怎么办？这个时候我们就可以给排序方法的key里面定规则，这个规则就是按照元素的第二个下标进行排序。

def get_first_items(element):
    return element[1]

sorted(l, key=get_first_items)

---
[('B毛不易', 29), ('C周杰伦', 44), ('A张学友', 62)]

我们这里定义了一个函数get_first_items, 其实做了一件很简单的事情，就是获得了element的第二个下标。

那么这里我们其实可以不用这样定义函数，而是直接用匿名函数。关于匿名函数，我在Python基础课里也有详细的讲到，大家可以回头去翻看一下。

sorted(l, key=lambda element: element[1])

那其实，element是一个输入参数，是一个变量，所以我们完全可以就简写一下就行：

sorted(l, key=lambda e: e[1])

然后我们再在后面多加一个切片操作：

sorted(l, key=lambda e: e[1], reverse=True)[:2]

---
[('A张学友', 62), ('C周杰伦', 44)]

不用在意那个reverse=True, 只是打开了反向排序，因为个人情感上不想去掉张学友。

好，那这个时候呢我们在前面加一个for，就可以拿到名字和age，而我们只需要age:

[age for name, age in sorted(l, key=lambda e: e[1], reverse=True)[:2]]

---
[62, 44]

这样我们就可以只取两个排序最靠前的年龄值，当然最后，就是mean，取平均值。

np.mean([age for name, age in sorted(l, key=lambda e: e[1], reverse=True)[:2]])

---
53.0

那我们之前所写的函数内容就是这样一段话，拆解之后是不是就能明白了？

那么刚才讲到的这种方法，你会发现它是在找相似的东西，其实我们定义的这种方法，后来给它起个名字叫做：发现K个最相近的邻居，K-Neighbor-Nearest, 简称KNN。

def knn(history_price, query_x, topn=3):
    return np.mean([p for x, p in sorted(history_price.items(), key=lambda x_y: (x_y[0] - query_x) **2)[:topn]])

这种算法之前机器学习的章节里咱们也详细讲过，这是一个非常经典的机器学习算法。关于KNN的有优点和缺点，我们之前也讲的很详细。那大家可以回过头取看我关于机器学习KNN的部分来学习，这里就不再继续赘述KNN的内容了，在这里，我们就了解之前我们所做的这么多内容，其实就是KNN，就可以了。

好，那这节课的内容就到这里，下一节课，咱们会继续写这一篇未完成的代码，来找到X_rm和y之间的函数关系。那么代码文件就依然还是18.ipynb。