一.概念
优先级队列是一种特殊类型的队列,它根据每个元素的优先级进行排序和访问。较高优先级的元素将在较低优先级的元素之前被处理。
优先级队列可以使用不同的数据结构实现,包括数组、链表或二叉堆。其中,二叉堆是实现优先级队列的常见选择。二叉堆是一个完全二叉树,具有以下特性:
- 每个节点的值都大于或等于其子节点的值(最大堆),或者每个节点的值都小于或等于其子节点的值(最小堆)。
- 二叉堆是一个完全二叉树,意味着除最后一层外,每一层都是满的,并且最后一层的节点都尽可能地靠左排列。
优先级队列的主要操作包括:
- 插入(add):将一个元素插入到队列中,并根据其优先级进行排序。
- 删除最高优先级元素(poll):从队列中删除具有最高优先级的元素。
- 查看最高优先级元素(peek):查看具有最高优先级的元素,而不删除它。
优先级队列在各个领域中的应用非常广泛,例如任务调度、数据压缩、网络路由等。
二.队列Queue接口
我们先定义好Queue接口,然后实现它
public interface Queue<E> {
/**
* 向队列尾添加元素
* @return 添加成功返回true,添加失败返回false
*/
boolean add(E e);
/**
* 从队列头删除一个节点,并取出该元素
* @return 队头元素
*/
E pull();
/**
* 从队列头取出该元素,但是不删除该节点
* @return 队头元素
*/
E peek();
/**
* 判断队列是否为空
* @return 空为true,非空为false
*/
boolean isEmpty();
/**
* 判断队列是否为满
* @return 满为true,不满为false
*/
boolean isFull();
}
三.优先级接口Proiroity,任务类Task
我们定义优先级接口Proiroity,它提供一个proiority()方法,获取元素的优先级
public interface Priority {
//返回优先级
int priority();
}我们定义任务类Task,作为放入优先级队列中的元素
/**
* 模拟任务类,有优先级的任务
*/
public class Task implements Priority{
String name;
int priority;
public Task(String name,int priority){
this.name = name;
this.priority = priority;
}
@Override
public int priority() {
return this.priority;
}
@Override
public String toString() {
return "Task{" +
"name='" + name + '\'' +
", priority=" + priority +
'}';
}
}
四.无序数组实现优先级队列
/**
* 无序数组实现优先级队列
* @param <E>
*/
public class DisOrderArrayPriorityQueue<E extends Priority> implements Queue<E>,Iterable<E> {
//数组
E[] array;
//元素的个数,也可以作为尾指针
int size;
@SuppressWarnings("all")
public DisOrderArrayPriorityQueue(int capacity){
array = (E[]) new Priority[capacity];
size = 0;
}
/**
* 返回优先级最大的索引位置
* @return
*/
private int maxPriority(){
int max = 0;
for (int i = 0; i < size; i++) {
if(array[max].priority() < array[i].priority()){
//将max索引设置为i
max = i;
}
}
return max;
}
/**
* 移除优先级最大的元素
*
* m
* 0 1 2 3 4 5 6
* a b c d e f g
*
* index=5,
*
* @param index
*/
private void remove(int index){
if(index < size){
//当该索引不是最后一个位置时需要移动数组
System.arraycopy(array,index+1,array,index,size-1-index);
}
//否则不需要移动数组
//都需要让size--;
size--;
}
/**
* 添加元素,直接在末尾添加就可以了
* @param e
* @return
*/
@Override
public boolean add(E e) {
//先判断是否满
if (isFull()) {
return false;
}
array[size] = e;
size++;
return true;
}
/**
* 移除优先级最大的元素
* @return
*/
@Override
public E pull() {
if(isEmpty()){
return null;
}
int max = maxPriority();
E e = array[max];
remove(max);
return e;
}
/**
* 返回优先级最大的元素
* @return
*/
@Override
public E peek() {
if(isEmpty()){
return null;
}
int max = maxPriority();
return array[max];
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean isFull() {
return size == array.length;
}
//遍历
@Override
public Iterator<E> iterator() {
return new Iterator<E>() {
int p = 0;
@Override
public boolean hasNext() {
return p != size;
}
@Override
public E next() {
E e = array[p];
p++;
return e;
}
};
}
}五.有序数组实现优先级队列
/**
* 有序数组实现优先级队列
* @param <E>
*/
public class OrderArrayPriorityQueue<E extends Priority> implements Queue<E> ,Iterable<E>{
E[] array;
int size;
@SuppressWarnings("all")
public OrderArrayPriorityQueue(int capacity){
array = (E[]) new Priority[capacity];
size = 0;
}
private void insertTo(E e){
int i = size - 1;
while ( i >= 0 && array[i].priority() > e.priority() ){
//将i后移
array[i+1] = array[i];
i--;
}
//插入到正确的位置
array[i+1] = e;
}
@Override
public boolean add(E e) {
if(isFull()){
return false;
}
//先插入到正确的索引位置
insertTo(e);
size++;
return true;
}
/**
* 移除优先级最高的元素(最后一个元素)
* @return
*/
@Override
public E pull() {
if(isEmpty()){
return null;
}
E e = array[size-1];
//让size--
size--;
array[size] = null; //help GC
return e;
}
/**
* 返回队列优先级最高的元素(最后一个元素)
* @return
*/
@Override
public E peek() {
if(isEmpty()){
return null;
}
return array[size-1];
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean isFull() {
return size == array.length;
}
//遍历
@Override
public Iterator<E> iterator() {
return new Iterator<E>() {
int p = 0;
@Override
public boolean hasNext() {
return p != size;
}
@Override
public E next() {
E e = array[p];
p++;
return e;
}
};
}
}六.无序数组和有序数组的区别
对于无序数组来说,每次添加元素是直接添加在数组的末尾,添加起来方便,但是取出优先级最高的元素需要进行一次排序,也就是取出复杂;
对于有序数组来说,每次取出优先级最高的元素就是取去数组末尾的元素,但是添加元素时,需要进行一次插入排序,找到合适的位置,也就是添加复杂
七.大顶堆实现优先级队列
1.大顶堆
2.基于数组的实现
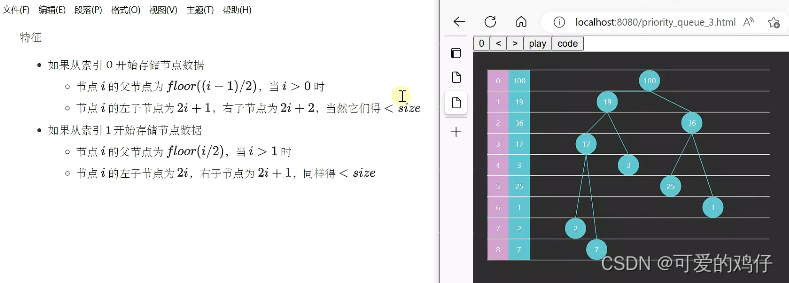
堆虽然是非线性的数据结构,但是我们可以利用数组来存储他的节点,这是有规律的,
节点i的父节点是floor((i-1)/2)
节点i的左子节点是2i + 1, 右子节点是2i + 2
下面我们用数组来实现堆的优先级队列
/**
* 数组实现大顶堆,实现优先级队列
* @param <E>
*/
public class HeapArrayPriorityQueue<E extends Priority> implements Queue<E> {
E[] array;
int size;
@SuppressWarnings("all")
public HeapArrayPriorityQueue(int capacity){
array = (E[]) new Priority[capacity];
size = 0;
}
/**
* 添加元素
*
* 1.首先将元素添加到数组的末尾
* 2.然后让size++;
* 3.然后调整堆使其符合大顶堆
*
*
* @param e
* @return
*/
@Override
public boolean add(E e) {
if(isFull()){
return false;
}
//先记录child的索引位置,就是在数组的末尾添加
int child = size++;
//找到他的父节点的索引位置
int parent = (child - 1)/2;
//然后比较要添加元素的优先级和parent的优先级
//而且child必须是大于0的,当child==0时,表示到堆顶了,就不需要再调整了
while ( child > 0 && e.priority() > array[parent].priority() ){
//当e的优先级大于parent的优先级时
//parent要向下沉到child处
array[child] = array[parent];
//然后将child的索引位置设置为parent
child = parent;
//继续找到child的父节点位置
parent = (child - 1)/2;
}
//调整完成后,child处就是要插入的正确位置
array[child] = e;
return true;
}
@Override
public E pull() {
if(isEmpty()){
return null;
}
//先交换0处和最后一个位置
swap(0,size-1);
size--;
E e = array[size];
array[size] = null; //help GC
//调整堆,也就是让堆顶元素下沉到合适的位置
adjust(0);
return e;
}
@Override
public E peek() {
if(isEmpty()){
return null;
}
return array[0];
}
/**
* 交换数组中两个索引位置的值
* @param i
* @param j
*/
private void swap(int i ,int j){
E e = array[i];
array[i] = array[j];
array[j] = e;
}
/**
* 调整堆,从堆顶开始
* @param parent
*/
private void adjust(int parent){
int left = parent * 2 + 1;
int right = left + 1;
//假设parent最大
int max = parent;
//分别判断左孩子,右孩子与parent的优先级
if(left > 0 && array[left].priority() > array[parent].priority()){
max = left;
}
if(right > 0 && array[right].priority() > array[parent].priority()){
max = right;
}
//如果max!=parent,就需要交换max和parent
if(max != parent){
swap(max,parent);
//递归调用,将max作为parent继续调用
adjust(max);
}
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean isFull() {
return size == array.length;
}
}