数据结构-栈和队列力扣题

news2024/11/23 4:33:53

目录

有效的括号

用队列实现栈

 用栈实现队列

 设计循环队列

有效的括号

题目链接：力扣（LeetCode）

思路： 这道题可以用栈来解决，先让字符串中的左括号' ( '，' [ '，' { '入栈，s指向字符串下一个字符，如果该字符也是左括号，那就继续入栈，如果是右括号，那就让其与栈顶元素相匹配（每次都要弹出栈顶元素），匹配上了，继续循环，匹配不上就返回false，注意在每次返回false之前都要销毁栈。

还要考虑极端情况，如果全是左括号，我们要在代码最后进行判空，不为空，返回false，同时，这次判空也能解决前面几对都匹配上，只有最后一个左括号没匹配上的问题（例如："()[]{}{"）。

如果全是右括号，说明整个过程中没有入栈元素，此时判空，如果为空返回false，同时，这次判空也能解决前面几对都匹配上，只有最后一个右括号没匹配上的问题（例如："()[]{}}"）。

如果用C语言来解题的话，栈需要自己写。

代码如下：

typedef int STDatatype;
typedef struct Stack
{
	STDatatype* a;
	int top;
	int capacity;
}ST;

//初始化栈
void STInit(ST* pst)
{
	assert(pst);
	pst->a = NULL;
	pst->top = 0;
	pst->capacity = 0;
}

//入栈
void STPush(ST* pst, STDatatype x)
{
	//开辟空间
	if (pst->top == pst->capacity)
	{
		int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
		STDatatype* tmp = (STDatatype*)realloc(pst->a, sizeof(STDatatype) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		pst->a = tmp;
		pst->capacity = newcapacity;
	}
	//插入
	pst->a[pst->top] = x;
	pst->top++;
}
//判空函数
bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}
//出栈
void STPop(ST* pst)
{
	assert(pst);
	assert(!STEmpty(pst));
	pst->top--;
}
//获取栈顶元素
STDatatype STTop(ST* pst)
{
	assert(pst);
	assert(!STEmpty(pst));
	return pst->a[pst->top - 1];
}
//获取栈中有效数据的个数
int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}
//销毁栈
void STDestory(ST* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;
	pst->top = pst->capacity = 0;
}


bool isValid(char* s) {
    ST st;
    STInit(&st);
    while(*s)
    {

        if(*s=='('||*s=='['||*s=='{')
        {
            STPush(&st,*s);
        }

        else
        {

            if(STEmpty(&st))
			{
			   STDestory(&st);
               return false;
			}


			char top=STTop(&st);
			STPop(&st);
						
            if((top!='('&&*s==')')
              ||(top!='['&&*s==']')
              ||(top!='{'&&*s=='}'))
            {

                STDestory(&st);
                return false;
            
            }
        }
				 ++s;
    }

	bool ret=STEmpty(&st);
	STDestory(&st);
    return ret;
}

用队列实现栈

题目链接：力扣（LeetCode）

 思路：队列是先入先出，栈是先入后出，要用队列实现栈，我们可以定义两个栈q1和q2，当它们都为空时，随便选一个存入数据，假设q1中有数据1 2 3 4，我们可以把q1中的1 2 3 push进q2中，然后把q1中的4 pop出去，接着把q2中的1 2 push进q1，然后把q2中的3 pop出去，这样循环在q1和q2中倒数据，就实现了4 3 2 1依次出栈，即先入后出。

当我们在出栈的同时，想要入栈，就把数据push进有数据的队列即可。

想要用C语言做这道题，队列的实现代码也要自己写。

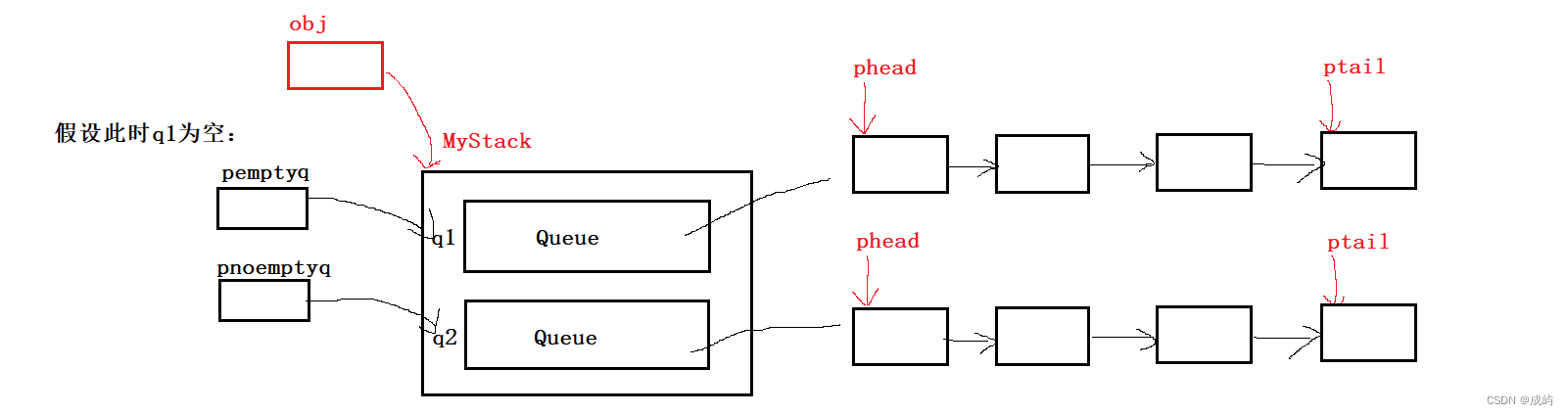
注意，我们下列代码是结构体的三层嵌套，所以销毁时要先销毁q1和q2，再销毁obj，如果只销毁obj，由于我们的队列q1和q2中分别有两个头尾指针还有节点，会造成内存泄漏的问题。

它们的关系图如下：

代码如下：

typedef int QDatatype;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDatatype data;
}QNode;

typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
}Queue;

//初始化队列
void QueueInit(Queue* pq)
{
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}

//队尾入队列
void QueuePush(Queue* pq, QDatatype x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return;
	}
	newnode->data = x;
	newnode->next = NULL;

	if (pq->ptail == NULL)
	{
		assert(pq->phead == NULL);
		pq->phead = pq->ptail=newnode;
	}
	else
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	pq->size++;
}

//判空函数
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->size ==0 ;
}

//队头出队列
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	//一个节点
	//多个节点
	if (pq->phead->next == NULL)
	{
		free(pq->phead);
		pq->phead = pq->ptail= NULL;
	}
	else
	{
		QNode* next = pq->phead->next;
		free(pq->phead);
		pq->phead = next;
	}
	pq->size--;
}

//获取队列头部元素
QDatatype QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->phead->data;
}

//获取队列尾部元素
QDatatype QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->ptail->data;
}

//获取队列中有效元素个数
int Queuesize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

//销毁队列
void DestoryQueue(Queue* pq)
{
	assert(pq);
	while (pq->phead)
	{
		QNode* next = pq->phead->next;
		free(pq->phead);
		pq->phead = next;
	}
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}


typedef struct {
    Queue q1;
    Queue q2;
} MyStack;


MyStack* myStackCreate() {

    MyStack* obj=(MyStack*)malloc(sizeof(MyStack));

    if(obj==NULL)
    {
        perror("malloc fail");
        return NULL;
    }

    QueueInit(&obj->q1);
    QueueInit(&obj->q2);
    return obj;

}

void myStackPush(MyStack* obj, int x) {

    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}

int myStackPop(MyStack* obj) {

    Queue* pemptyq=&obj->q1;
    Queue* pnoemptyq=&obj->q2;

    if(!QueueEmpty(&obj->q1))
    {
        pemptyq=&obj->q2;
        pnoemptyq=&obj->q1;
    }

    while(Queuesize(pnoemptyq)>1)
    {
        QueuePush(pemptyq,QueueFront(pnoemptyq));
		QueuePop(pnoemptyq);
    }

    int top=QueueFront(pnoemptyq);
    QueuePop(pnoemptyq);
    return top;

}

int myStackTop(MyStack* obj) {

    if(!QueueEmpty(&obj->q1))
        return QueueBack(&obj->q1);
	else
		return QueueBack(&obj->q2);

}

bool myStackEmpty(MyStack* obj) {

    assert(obj);
    return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);

}

void myStackFree(MyStack* obj) {

   	DestoryQueue(&obj->q1);
	DestoryQueue(&obj->q2);
    free(obj);
}

 用栈实现队列

题目链接：力扣（LeetCode）

思路：这道题用上道题的思路也能实现，但是过于复杂。

简单思路：我们定义两个栈pushst和popst，栈中数据遵循先入后出的原则，如果在pushst中push进去1 2 3 4，那他从栈顶到栈底依次是 4 3 2 1 ，但是如果我们把pushst中的数据再push进popst中，那popst中从栈顶到栈底依次是 1 2 3 4，此时我们只要将popst中的数据按照栈本身先入后出的原则pop出去，就是1 2 3 4，这样就实现了先入先出。如下图：

当我们在出队列的同时，想要入队列，要先等popst中的数据出完才行，所以当popst为空，pushst不为空时，才能把pushst中的数据往popst中push。

代码如下：

typedef int STDatatype;
typedef struct Stack
{
	STDatatype* a;
	int top;
	int capacity;
}ST;

//初始化栈
void STInit(ST* pst)
{
	assert(pst);
	pst->a = NULL;
	pst->top = 0;
	pst->capacity = 0;
}

//入栈
void STPush(ST* pst, STDatatype x)
{
	//开辟空间
	if (pst->top == pst->capacity)
	{
		int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
		STDatatype* tmp = (STDatatype*)realloc(pst->a, sizeof(STDatatype) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		pst->a = tmp;
		pst->capacity = newcapacity;
	}
	//插入
	pst->a[pst->top] = x;
	pst->top++;
}
//判空函数
bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}
//出栈
void STPop(ST* pst)
{
	assert(pst);
	assert(!STEmpty(pst));
	pst->top--;
}
//获取栈顶元素
STDatatype STTop(ST* pst)
{
	assert(pst);
	assert(!STEmpty(pst));
	return pst->a[pst->top - 1];
}
//获取栈中有效数据的个数
int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}
//销毁栈
void STDestory(ST* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;
	pst->top = pst->capacity = 0;
}
typedef struct {
    ST pushst;
    ST popst;
} MyQueue;


MyQueue* myQueueCreate() {
    MyQueue*obj=(MyQueue*)malloc(sizeof(MyQueue));
    if(obj==NULL)
    {
        perror("malloc fail\n");
        return NULL;
    }
    STInit(&obj->pushst);
    STInit(&obj->popst);
    return obj;
}

void myQueuePush(MyQueue* obj, int x) {
        STPush(&obj->pushst,x);
}

int myQueuePop(MyQueue* obj) {
   int front= myQueuePeek(obj);
   STPop(&obj->popst);
   return front;
}

int myQueuePeek(MyQueue* obj) {
    if(STEmpty(&obj->popst))
    {
        while(!STEmpty(&obj->pushst))
        {
        STPush(&obj->popst,STTop(&obj->pushst));
        STPop(&obj->pushst);
        }
    }
    return STTop(&obj->popst);
}

bool myQueueEmpty(MyQueue* obj) {
    assert(obj);
    return STEmpty(&obj->pushst)&&STEmpty(&obj->popst);
}

void myQueueFree(MyQueue* obj) {
    STDestory(&obj->pushst);
    STDestory(&obj->popst);
    free(obj);
}

 设计循环队列

题目链接：力扣（LeetCode）

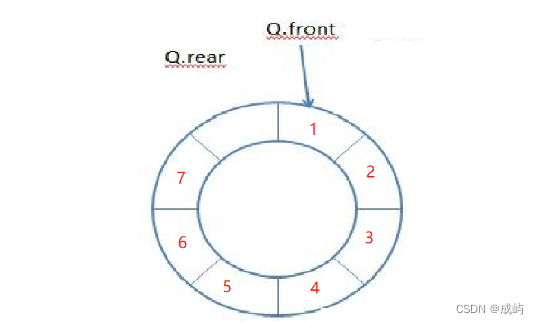
思路： 本题用数组队列和链表队列都能实现，在这里我们使用数组队列，首先，要设计一个循环队列，我们就要知道队列什么时候满，什么时候空，空很容易判断，当front=rear时就为空，问题是当我们循环一圈以后，队列已经满了，但此时front也等于rear，所以为了不发生混淆，我们在开辟空间时多开辟一块，假设要存7个数据就开辟8个空间：

此时当rear+1==front时就为满。但这只是上图为了形象展示，实际上在数组中，每存一个数，rear++，但是数组首尾并没有相连，不能用rear+1==front判断是否满了，我们可以用下标rear，当(rear+1)%(k+1)==front时就说明队列满了。

而要在队列中插入数据，每次插入之后下标rear++，但是当队列满了之后，rear就是数组中最后一个下标，这时如果我们在队头出了两个数据，想再往队列里插数据，就要让rear回到开始的位置，所以每次rear++后，让rear=rear%(k+1)，此时再插入，就形成了一个完美的循环，同理，删除数据也一样，每次删完都让front=front%(k+1)。

obj->a[(obj->rear+obj->k)%(obj->k+1)]这段代码是为了返回队尾元素。

代码如下：

typedef struct {
    int front;
    int rear;
    int k;
    int*a;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue*obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->front=obj->rear=0;
    obj->k=k;
    return obj;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {

    return obj->front==obj->rear;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->rear+1)%(obj->k+1)==obj->front;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if( myCircularQueueIsFull(obj))
    return false;
    obj->a[obj->rear]=value;
    obj->rear++;
    obj->rear=(obj->rear)%(obj->k+1);
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    return false;
    obj->front++;
    obj->front=(obj->front)%(obj->k+1);
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    return -1;
    else
    return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    return -1;
    else
    return obj->a[(obj->rear+obj->k)%(obj->k+1)];
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

栈与队列的内容到这里就结束了，下节开始学习堆与二叉树，

未完待续。。。 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1190425.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

昇腾CANN 7.0 黑科技：大模型推理部署技术解密

昇腾CANN 7.0 黑科技：大模型推理部署技术解密

CANN作为最接近昇腾AI系列硬件产品的一层，通过软硬件联合设计，打造出适合昇腾AI处理器的软件架构，充分使能和释放昇腾硬件的澎湃算力。针对大模型推理场景，CANN最新发布的CANN 7.0版本有机整合各内部组件，支持大模型的…
阅读更多...
笔记本电脑的麦克风没有声音

笔记本电脑的麦克风没有声音

笔记本电脑的麦克风没有声音是一个常见的问题，可能是由于以下几个原因导致的： 第一，麦克风没有启用或者被禁用了。在Windows系统中，右键单击任务栏上的音量图标，选择“录音设备”，在弹出窗口中找到麦克风&a…
阅读更多...
阿里云Intel Xeon Platinum可扩展处理器性能说明

阿里云Intel Xeon Platinum可扩展处理器性能说明

阿里云Intel Xeon Platinum可扩展处理器性能如何？目前云服务器ECS经济型e实例采用该款CPU型号，正好阿里云服务器网购买了一台2核CPU、2G内存、3M固定带宽、40G ESSD Entry云盘，一年优惠价99元，第二年续费不涨价依旧是99元一年&…
阅读更多...
2023最新版JavaSE教程——第3天：流程控制语句之顺序语句与分支语句

2023最新版JavaSE教程——第3天：流程控制语句之顺序语句与分支语句

目录 一、顺序结构二、分支语句2.1 if-else条件判断结构2.1.1 基本语法2.1.2 应用举例2.1.3 if...else嵌套2.1.4 其它说明2.1.5 练习 2.2 switch-case选择结构2.2.1 基本语法2.2.2 应用举例2.2.3 利用case的穿透性2.2.4 if-else语句与switch-case语句比较2.2.5 练习 流程控制语…
阅读更多...
windows上 Nexus 批量上传 maven依赖npm依赖

windows上 Nexus 批量上传 maven依赖npm依赖

windows上 Nexus 批量上传 maven依赖/npm依赖 前言：windows系统上要有git环境，不然sh文件执行不了 1.批量上传maven依赖 设置脚本，把脚本放在依赖包的根目录执行，脚本名为upload.sh #!/bin/bash# 定义变量 while getopts &quo…
阅读更多...
陪玩2.0升级版源码/价值18500元的最新商业版游戏陪玩语音聊天系统源码

陪玩2.0升级版源码/价值18500元的最新商业版游戏陪玩语音聊天系统源码

陪玩2.0升级版源码，价值18500元的最新商业版游戏陪玩语音聊天系统源码。 修复部分逻辑以及bug 修复bug：店员拒单后，退款会退到店员账号里而不是用户账户里。 修复bug：客户在盲盒下单后，马上取消了订单，但…
阅读更多...
Java进阶（JVM调优）——JVM调优参数 JDK自带工具使用 内存溢出和死锁问题案例 GC垃圾回收

Java进阶（JVM调优）——JVM调优参数 JDK自带工具使用 内存溢出和死锁问题案例 GC垃圾回收

前言 JVM作为Java进阶的知识，是需要Java程序员不断深度和理解的。 本篇博客介绍JVM调优的相关知识，给出了一个demo案例，介绍了JVM调优的主要参数；介绍了jdk自带的jvm分析工具的使用；给出了一个内存溢出的调优场景&am…
阅读更多...
Blender做一个小凳子学习笔记

Blender做一个小凳子学习笔记

文章目录 创建椅座椅子腿靠背渲染 本文是这个B站视频的学习笔记：【Blender】爆肝两个月！拜托三连了！这绝对是全B站最用心的（没有之一）Blender 3D建模零基础入门 创建椅座 首先，需要了解其左上角和右上角的…
阅读更多...
为什么很多人从FPGA转IC前端岗?哪个前景好？

为什么很多人从FPGA转IC前端岗?哪个前景好？

很多入行不久的朋友潜意识里会认为FPGA是很高深的东西，能掌握FPGA的一定都是极其厉害的人。 其实，这是一个误解。 我们所讨论的FPGA只是基于已有的FPGA芯片去做后端排列组合的工作内容，而不是设计制造新的FPGA芯片，世界上能做这…
阅读更多...
【数字通信原理】第六章 频带传输及调制原理

【数字通信原理】第六章 频带传输及调制原理

第六章 数字频带传输系统 1. 二进制数字调制，解调原理:2ASK,2FSK 2.二进制数字调制，解调原理:2PSK,2DPSK 3.二进制数字已调信号的功率谱 3. 二进制数字调制系统的抗噪声性能
阅读更多...
cookie 里面都包含什么属性？

cookie 里面都包含什么属性？

结论先行： Cookie 中除了名称和值外，还有几个比较常见的，例如： Domain 域：指定了 cookie 可以发送到哪些域，只有发送到指定域或其子域的请求才会携带该cookie； Path 路径：指定哪些…
阅读更多...
(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明

(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明

文章目录 系统说明openEuler23.03系统手动配置ip流程修改名称生成网卡配置文件【openEuler23.03系统添加网卡文件配置流程】手动指定ip添加ipv6地址修改配置文件信息和名称删除创建的网卡信息重启网卡生效并测试 openEuler23.03系统网络管理说明 系统说明 我这用云上最小化安装…
阅读更多...
网络编程套接字（3）——协议定制 | 序列化与反序列化

网络编程套接字（3）——协议定制 | 序列化与反序列化

文章目录 一.认识“协议”1.协议的概念2.结构化数据的传输3.序列化和反序列化 二. 网络版计算器1.服务端2.协议定制(1) 网络发送和读取的正确理解(2) 协议定制的问题 3.客户端4.代码 三.Json实现序列化反序列化1.简单介绍2.使用 一.认识“协议” 1.协议的概念 协议&#xff0c…
阅读更多...
【Proteus仿真】【Arduino单片机】简易计算器设计

【Proteus仿真】【Arduino单片机】简易计算器设计

文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真Arduino单片机控制器，使用PCF8574、LCD1602液晶、4*4矩阵键盘等。 主要功能： 系统运行后，操作矩阵按键可实现简单四则运算。 二、软件设计 /* …
阅读更多...
【修车案例】一波形一案例（9）

【修车案例】一波形一案例（9）

故障车型：捷豹X-Type 故障现象：发动机故障指示灯点亮，加速时动力不足，扫描工具显示EGR阀和涡轮增压器增压控制位置传感器电路故障 示波器诊断：检测增压控制位置传感器电路的完整性 A通道 - 增压控制执行电机电源电压B通…
阅读更多...
20行JS代码实现屏幕录制

20行JS代码实现屏幕录制

在开发中可能有遇到过屏幕录制的需求，无论是教学、演示还是游戏录制，都需要通过屏幕录制来记录和分享内容。一般在App内H5页基于客户端能力实现的较多，现在浏览器中的 MediaRecorder 也提供了这种能力。MediaRecorder 是一种强大的技术&#…
阅读更多...
【JS】scrollTop+scrollHeight+clientTop+clientHeight+offsetTop+offsetHeight

【JS】scrollTop+scrollHeight+clientTop+clientHeight+offsetTop+offsetHeight

scrollTop、scrollHeight、clientTop、clientHeight、offsetTop以及offsetHeight 1. scrollTop 与 scrollHeight 1.1 scrollTop scrollTop 是这六个属性中唯一一个可写的属性。 Element.scrollTop 属性可以获取或设置一个元素的内容垂直滚动的像素数。 一个元素的 scrollT…
阅读更多...
2023年破圈：盘点11个新零售商业模式，永远不再打商业价格战

2023年破圈：盘点11个新零售商业模式，永远不再打商业价格战

2023年破圈：盘点11个新零售商业模式，永远不再打商业价格战 前沿：纵观今年互联网各种类型项目，基本都是又短又快，但依然也有风靡的短跑冠军，那么互联网的项目能否跑的长久，是否是商业模式的原因&…
阅读更多...
Linux学习第37天：Linux I2C 驱动实验：哥俩好

Linux学习第37天：Linux I2C 驱动实验：哥俩好

Linux版本号4.1.15 芯片I.MX6ULL 大叔学Linux 品人间百味 思文短情长 世界上的很多事物都是成双成对出现的。也包括在驱动开发的过程中，比如I2C中其实就是数据线和时钟线的相互配合才能完成的。 I2C常用于连接各种外设、…
阅读更多...
开发知识点-Django

开发知识点-Django

Django 1 了解简介2 Django项目结构3 url 地址 和视图函数4 路由配置5 请求及响应6 GET请求和POST请求查询字符串 7 Django设计模式及模板层8 模板层-变量和标签9 模板层-过滤器和继承继承 重写 10 url反向解析11 静态文件12 Django 应用及分布式路由创建之后 注册 一下 13 模型…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023