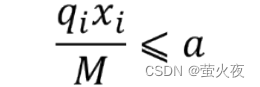线性规划 

优化类问题：有限的资源，最大的收益

例子:

华强去水果摊找茬，水果摊上共3个瓜，华强总共有40点体力值,每劈一个瓜能带来40点挑衅值,每挑一个瓜问“你这瓜保熟吗”能带来30点挑衅值,劈瓜消耗20点体力值，问话消耗10点体力值, 问如何利用这些瓜，使挑衅值最大？

注意:遇到不懂的词汇去百度搜，去查文献，尽快了解问题背景, 遇到大量陌生专有名词就尽量别选, 例如国赛A题

分析: 

 注意x1>=0和x2>=0这两个隐藏条件, 可能会对解答有影响

线性规划模型三要素: 

 线性规划模型:

 题目类型:

题目中提到“XXX有多少多少”“怎样安排/分配”“最多(少)”“利润最大”等词；

生产安排：

原材料、设备有限制，总利润最大
• 若生产两种机床，利润分别为XXX；A机器和B机器加工，有顺序要求，有不同损耗费用，不同的工作时间…；问题：怎样安排生产使得总利润最大？

投资收益：

涉及资产配置、收益率、损失率、组合投资，总收益最大
• 若总资金为M，有n种资产可以配置
• 每种资产的平均收益率…，风险损失率…，手续费…；问题：设计组合投资方案，使得收益尽可能大，总体风险尽可能小（本质是多目标规划，可化简为一个目标的线性规划） 

销售运输：

产地、销地、产量、销量、运费，总运费最省
• 商品有m个产地和n个销地，需要从产地运到销地
• 各产地的产量…，各销地需求量…由a产地运到b销地的运价xxx；问题：如何调运才能使总运费最省？

车辆安排：

路线、起点终点、承载量、时间点、车次安排最合理
• 不同种类的车辆有各自的承载量，工地各点之间要安排车辆运输
• 工地里有多条路线……满足用工需求的情况下…；问题：如何安排车辆能使产量尽可能大？

注意:最合理这种模糊词需要给出准确的数学定义, 可能是利润最大, 排队时间最短, 运载量最大....

投资类问题的注意事项

• 收益率 = 收益/成本，设收益率为r，收益为g，成本为c
• 如果要求“总收益最大”，一般可以用线性规划
• 如果要求“总收益率最大”，一般是非线性规划, r = g/c, 其中c是-1次方（不绝对） 

判断标准

判断的标准就是建立的模型中, 约束条件和目标函数中的变量是否全是一次方
• 如果成本c为变量，追求r最大，目标函数是 max r = g/c，其中变量c的次幂是-1，为非线性
如果成本c始终为常数, 总收益率就变成了线性规划

例题

 问题：给该公司设计一种投资组合方案，用给定的资金M，有选择地购买若干种资产或存银行生息，使净收益尽可能大，总体风险尽可能小。

问题分析

有目标函数（净收益尽可能大、总风险尽可能小）
有约束条件（总资金有限，和隐含数学条件：每一笔投资都是非负数） 

基本假设

由于投资数额M相当大，而题目设定的定额ui相对M很小,pi*ui更小,因此假设每一笔交易额xi都大于对应的定额ui

---

模型的建立 

决策变量: 投资项目si 的资金为xi (i = 0,1,2,3,4), 总收益Q

目标函数: 净收益尽可能大(max)、总风险尽可能小(min) (所以这是一个多目标线性规划模型)

约束条件: 投资总额为M、每一笔投资非负数

 目标函数

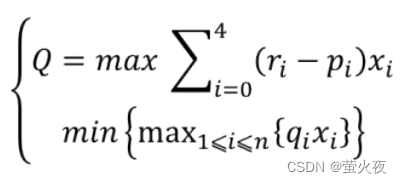
净收益尽可能大(max): 总收益=max(∑每一项的资金×(每一项的收益率-费率))

总风险尽可能小(min):  每一项的资金×风险率的最大值最小

约束条件 

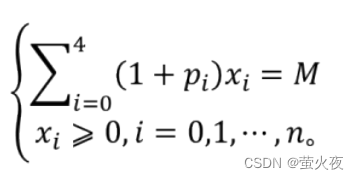
 ∑每一项的资金和交易费 = 总资金

每一笔投资都是非负数

---

合理的简化，事半功倍 

模型的简化:

现实中，不同人所能承受的风险不同
设某一类投资者，能接受的最大投资风险率为定值a
只要风险率小于等于该定值a，可视为对该类投资者满足“总风险尽可能小”即风险率

（风险率=投资额*损失率/总资产）满足:

分情况讨论:设低风险投资者能接受的a=5%，中风险投资者能接受的a=15%等等

基于该简化,将目标函数: 转化为了约束条件:

---

完成模型的建立

决策变量:  xi(i = 0,1,2,3,4), 第i种资产的投资额

目标函数和约束条件:

注意,除了xi(5个变量）,其他都是常数
显然,所有变量都是线性的, 因此这是一个（单目标）线性规划模型 

---

模型的建立到求解 

 建立模型时留下的坑

题目要求“总风险尽可能小”
本模型简化为只要风险率小于等于该定值a, 可视为对某一类投资者满足“总风险尽可能小’·模型中的a是一个常数，而不是变量，所以才能在写代码时套用matlab的函数

求解问题时尽量把坑填上(在论文里写作“模型改进”)

现实中的a是一个变量,不同投资者对风险的接受程度肯定不一样
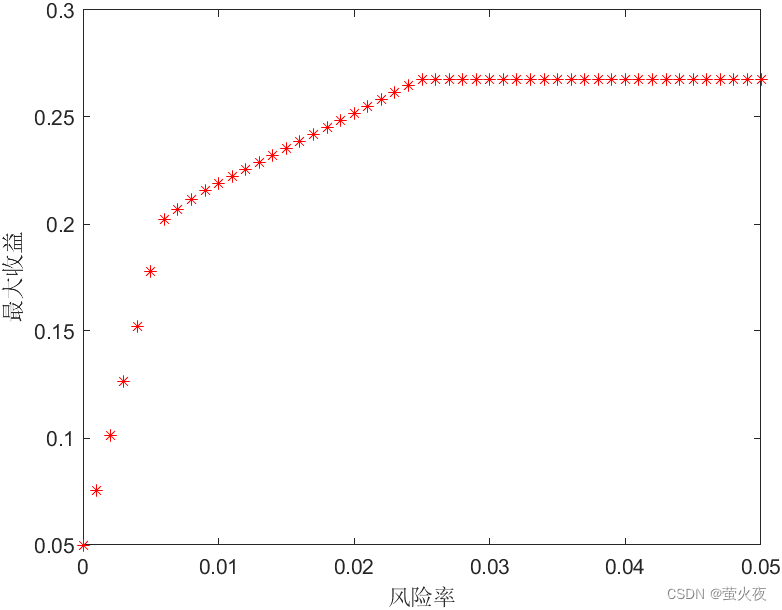
低风险投资者追求落袋为安, 对应a=5%;高风险投资者追求富贵险中求, 可能对应a=50%·那么在求解时, 对不同a取值分别进行求解（该操作实现了把a作为了“变量”) 

---

代码:

linprog函数使用具体分析:​​​​​​​Matlab线性规划函数linprog-小白详解_浩浩的科研笔记的博客-CSDN博客

linprog函数求解线性规划模型, linprog函数中的变量必须是matlab标准型(求最大值转化为求负的最小值, 约束条件是大于变换为小于)

函数：[x,fval]= linprog(f,A,b,Aeq,beq,lb,ub)

 

% clc是清除命令行窗口，clear是清除存储空间的变量
clc,clear;

%a矩阵的元素是不同的风险率,从0到0.05等差取值,相邻的两个数相差0.001
a = (0:0.001:0.05);

%目标函数的系数向量,因为求的是M的最大值,所以变为求-M的最小值,系数变为负
f = [-0.05,-0.27,-0.19,-0.185,-0.185]; 

%A是不等式约束条件的变量系数构成的矩阵
A = [0,0.025,0,0,0;
     0,0,0.015,0,0;
     0,0,0,0.055,0;
     0,0,0,0,0.026];
 %还可以这样构造A矩阵 A = [zeros(4,1),diag([0.025,0.015,0.055,0.026])]
 %用zeros先构造4行1列的全是0的矩阵,因为x0没有风险率系数为0
 %再构造对角矩阵,对角线上的元素为约束条件中的变量x1 x2 x3 x4的系数
 
 %等式约束的系数矩阵
 Aeq = [1 1.01 1.02 1.045 1.065];
 
 %M设为1
 beq = 1;
 
 %xi的下界
 lb = [0;0;0;0;0];
 
 %初始化保存最优解的Q矩阵,现在还没求出最优解先初始化为0
 Q = zeros(1,length(a));
 
 %XX用来存不同风险率下的最优解
 XX = [];
 
 for i = 1:length(a)
     b = a(i)*ones(4,1); %b是约束条件中的常数项矩阵,4行1列,每个元素都是a
     [x,y] = linprog(f,A,b,Aeq,beq,lb); %x是对应的投资分配xi,是列向量的形式
     Q(i) = -y; %-y是总收益的最大值
     XX = [XX;x']; %每次更新XX矩阵,保存每一个a值下的投资分配
 end

plot(a,Q,"*r");
xlabel('风险率');        % x和y轴分别附上标签
ylabel('最大收益');

​​​​​​​