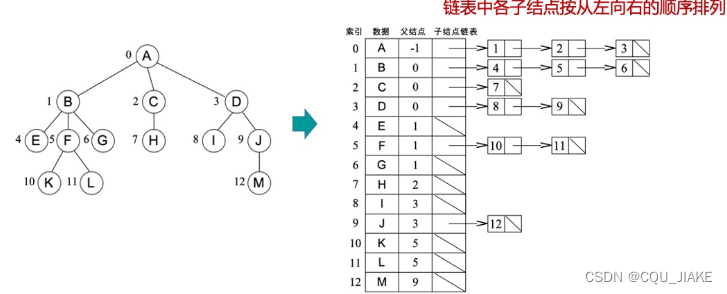
父亲表示法

优缺点:利用了树中除根结点外每个结点都有唯一的父节点这个性质,很容易找到树根,但是找孩子需要遍历整个线性表。


最近公共祖先
第一种方法,找路径然后比较
如果是搜索树,可以二分查找

不是,就dfs

第二种,不找路径
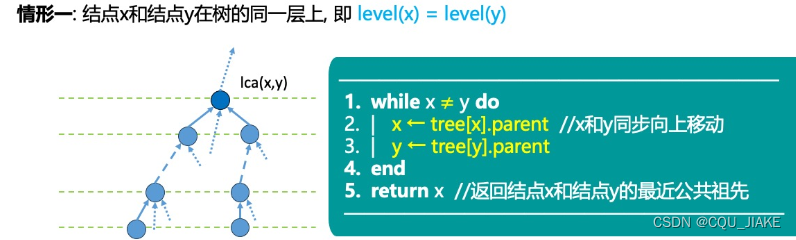
如果在同一层,那么就同步移动
如果不在同一层,
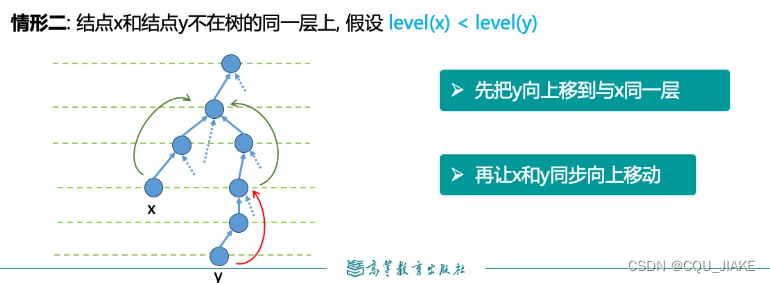
如果不在同一层,就让层数深的上升到层数浅的同一层,之后就是回到第一种情况,判断只要不相同,那么就接着同步往上走



经过这步,tx,ty同步向上,一个到根节点后,那么另一个还没到,它到根节点的距离,就是x与y的距离差值,如果ty<0,那就说明y先到根,y处于浅层,交换一下,就是让x处于浅层,y处于深层,并把ty赋值为tx,此时ty到根的距离就代表y和x之间的距离差

这步就是把深层结点往浅层结点走,Ty到根节点时,y就到了和x的同一层
孩子表示法
struct node
{
char data;
tree child[m]//m个孩子
};
tree t;
缺陷:只能从父结点遍历到子结点,不能从某个子结点返回到父结点。
孩子兄弟表示法
struct node{
char data;
tree firstchild,next;
}
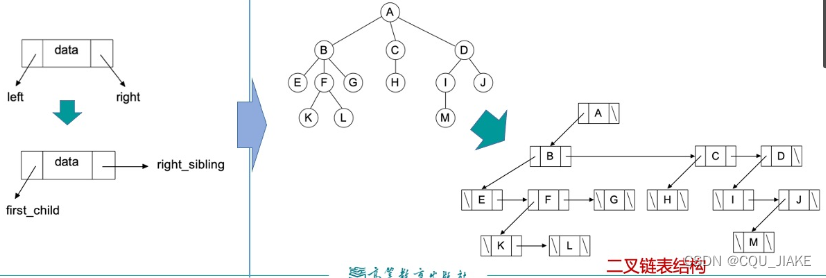
左孩子,右兄弟
树与二叉树的转换

森林与二叉树转换
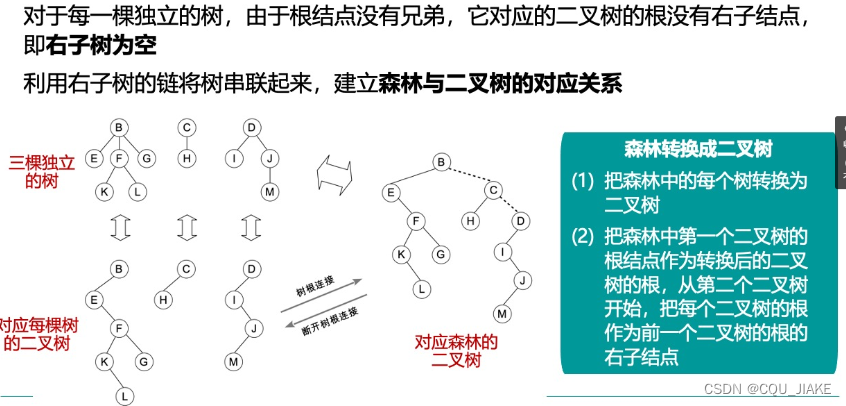
查找树的指定结点

左孩子,右兄弟,所以先找自己,自己的数据不对,找左孩子,如果没找到,那么node为空指针,则找右兄弟,即前序遍历
树与对应二叉树的遍历
void tral(tree t ,int m)
{
if(t)
{
cout<data<<endl;
for(int i=0;i<m;i++)
tral(t->child[i],m) //m为孩子的个数
}
}
树的遍历方案

树没有中序遍历,因为没有中的概念。前序就是先访问树根,再孩子;后序是先孩子,再根
注意下图M的位置标错了,应该是J的孩子而不是I的孩子

递归后序到F时,由于同样要后序,所以就先KL,最后在F,F完了再G
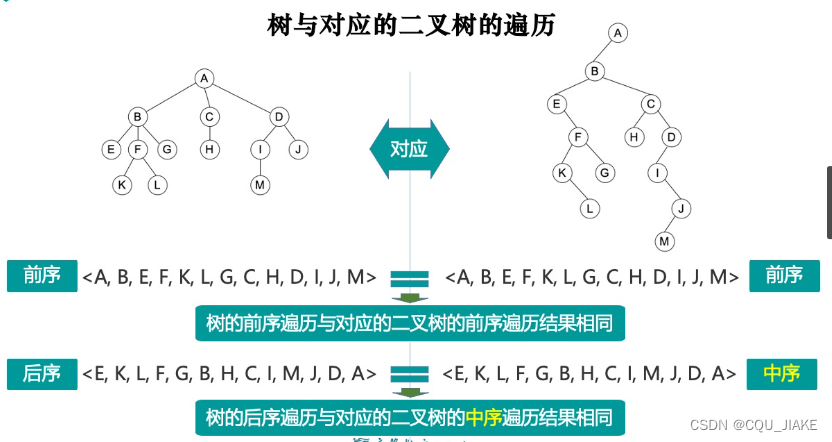

层序遍历树

森林遍历

前缀树

决策树
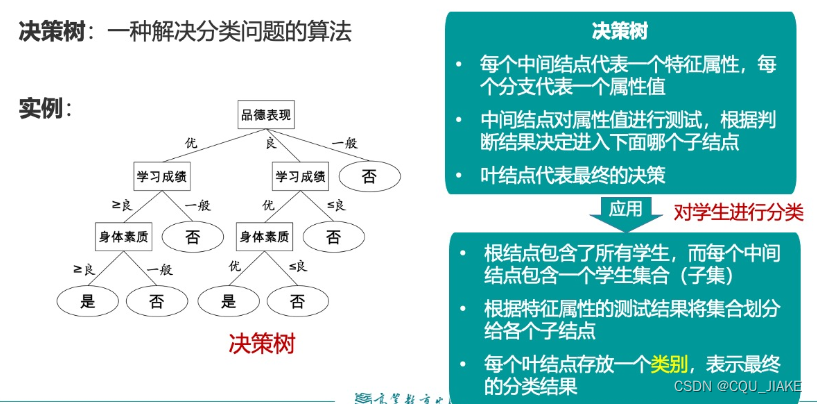

ID3算法




二叉搜索树插入
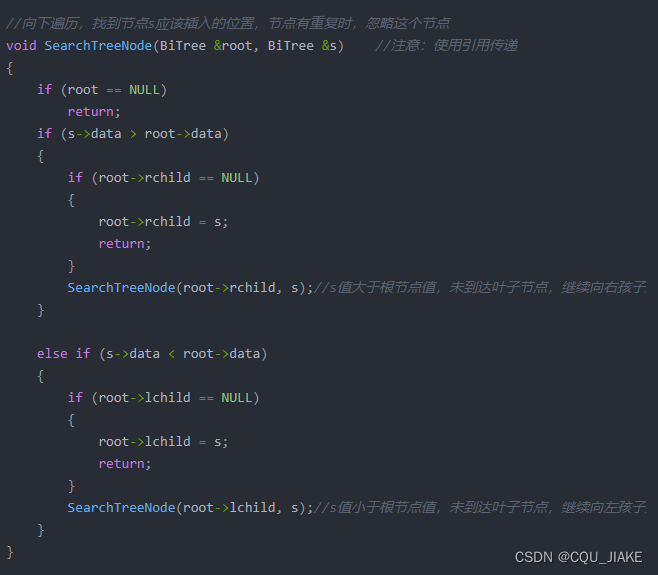
包装了一下
//插入一个节点,树为空,插入节点即为根节点,否则找合适的位置插入
void InsertNode(BiTree &tree, BiTree &s) //注意:使用引用传递
{
if (tree == NULL)
tree = s;
else
SearchTreeNode(tree, s);
}
//二叉排序树创建,每次增加一个结点,插到现有的二叉树上去
void CreateOrderBinaryTree(BiTree &tree, int *a)
{
for (int i = 0; i < len; i++)
{
BiTree s = (BiTree)malloc(sizeof(BiTNode));
s->data = a[i];
s->lchild = NULL;
s->rchild = NULL;
InsertNode(tree, s);
}
}
树
typedef struct BiTNode
{
ElemType data;
struct BiTNode *lchild, *rchild;
} *BiTree;
typedef struct Node
{
BiTree btnode;
bool isfirst;
}*node;
非递归遍历
//非递归前序遍历
void ProOrder(BiTree pRoot)
{
if (pRoot == NULL)
return;
BiTree p = pRoot;
stack<BiTree>s;
while (p != NULL || !s.empty())
{
while (p != NULL)
{
s.push(p);
cout << p->data << " "; //第一次遇见的时候输出
p = p->lchild;
}
if (!s.empty())
{
p = s.top();
s.pop();
p = p->rchild;
}
}
}
//非递归中序遍历
void midOrder(BiTree pRoot)
{
if (pRoot == NULL)
return;
BiTree p = pRoot;
stack<BiTree>s;
while (p != NULL || !s.empty())
{
while (p!=NULL)
{
s.push(p);
p = p->lchild;
}
if (!s.empty())
{
p = s.top();
cout << p->data << " "; //第二次遇见的时候输出
s.pop();
p = p->rchild;
}
}
}
//非递归实现后续遍历
void postOrder(BiTree pRoot)
{
if (pRoot == NULL)
return;
stack<node>s;
BiTree p = pRoot;
node tmp;
while (p!=NULL || !s.empty())
{
while (p != NULL) //沿左子树一直往下搜索,直至出现没有左子树的结点
{
node btn = (node)malloc(sizeof(Node));
btn->btnode = p;
btn->isfirst = true;
s.push(btn);
p = p->lchild;
}
if (!s.empty())
{
tmp = s.top();
s.pop();
if (tmp->isfirst == true) //第一次出现在栈顶
{
tmp->isfirst = false;
s.push(tmp);
p = tmp->btnode->rchild;
}
else //第二次出现在栈顶
{
cout << tmp->btnode->data<<" ";
p = NULL;
}
}
}
}
//非递归实现后续遍历
void postorder(BiTree pRoot)
{
if (pRoot == NULL)
return;
stack<BiTree>s;
BiTree cur = pRoot, pre = NULL;
s.push(pRoot);
while (!s.empty())
{
cur = s.top();
if ((cur->lchild == NULL&&cur->rchild == NULL) ||
((pre == cur->lchild || pre == cur->rchild) && pre != NULL))
{
cout << cur->data << " ";
s.pop();
pre = cur;
}
else
{
if (cur->rchild != NULL)
s.push(cur->rchild);
if (cur->lchild != NULL)
s.push(cur->lchild);
}
}
}