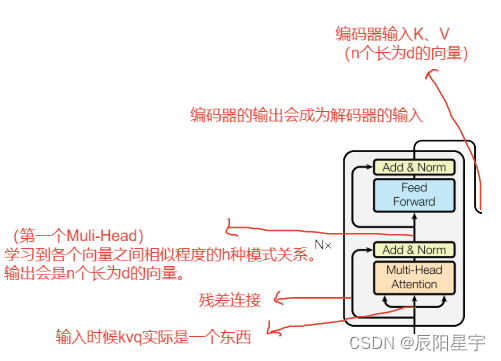
Encoder组件
编码器部分:
- 由N个编码器层堆叠而成
- 每个编码器层由两个子层连接结构组成
- 第一个子层连接结构包括一个多头自注意力子层和规范化层以及一个残差连接
- 第二个子层连接结构包括一个前馈全连接子层和规范化层以及一个残差连接
(1)Mask掩码张量
掩码张量:掩代表遮掩,码就是我们张量中的数值,它的尺寸不定,里面一般只有1和0的元素,代表位置被遭掩或者不被遮掩,至于是0位置被遮掩还是1位置被遭掩可以自定义,因此它的作用就是让另外一个张量中的一些数值被遮掩,也可以说被替换它的表现形式是一个张量。
作用: 通过预测遮掩的内容,来评估模型的预测能力。
在transformer中,掩码张量的主要作用在应用attention时,有一些生成的attention张量中的值计算有可能已知了未来信息而得到的,未来信息被看到是因为训练时会把整个输出结果都一次性进行Embedding,但是理论上解码器的的输出却不是一次就能产生最终结果的,而是一次次通过上一次结果综合得出的,因此,未来的信息可能被提前利用。所以,我们会进行遮掩。关于解码器的有关知识将在后面的章节中讲解。
1)先导示例
np.triu(matrix, k)示例:
np.triu(matrix, k):产生上三角矩阵,其中k控制产生零的对角线划分线位置。
k=0时候,对角线在主对角线,主对角线以下元素全变成0。
k=-1时候,对角线在主对角线向下移动一个位置。
k=1时候,对角线在主对角线向上移动一个位置。

np.triu([[1,2,3],[4,5,6],[7,8,9]], k=-1)
array([[1, 2, 3],
[4, 5, 6],
[0, 8, 9]])
np.triu([[1,2,3],[4,5,6],[7,8,9]], k=0)
array([[1, 2, 3],
[0, 5, 6],
[0, 0, 9]])
np.triu([[1,2,3],[4,5,6],[7,8,9]], k=1)
array([[0, 2, 3],
[0, 0, 6],
[0, 0, 0]])
使用1减去上三角矩阵,就会变成下三角矩阵
np.triu(np.ones(3), k=1)
array([[0., 1., 1.],
[0., 0., 1.],
[0., 0., 0.]])
1 - np.triu(np.ones(3), k=1)
array([[1., 0., 0.],
[1., 1., 0.],
[1., 1., 1.]])
2)subsequent_mask向后遮掩掩码函数实现
主要就是做一个下三角矩阵,掩码后续的词。分为三步走:
(1)定义掩码张量形状
(2)生成上三角矩阵
(3)用一减去上三角矩阵,形成下三角矩阵
def subsequent_mask(size):
# 定义掩码张量的形状
attn_shape = (1, size, size)
# 生成上三角矩阵,是其中的数据类型变为无符号的8位整形uint8
triu_mask = np.triu(np.ones(attn_shape), k = 1).astype('uint8')
# 进行三角反转,让上三角变成下三角,实现掩码当前位置之后的数
return torch.from_numpy(1 - triu_mask)
示例
# subsequent_mask示例
size = 5
sm = subsequent_mask(size)
plt.figure(figsize=(5, 5))
plt.imshow(subsequent_mask(20)[0])
tensor([[[1, 0, 0, 0, 0],
[1, 1, 0, 0, 0],
[1, 1, 1, 0, 0],
[1, 1, 1, 1, 0],
[1, 1, 1, 1, 1]]], dtype=torch.uint8)
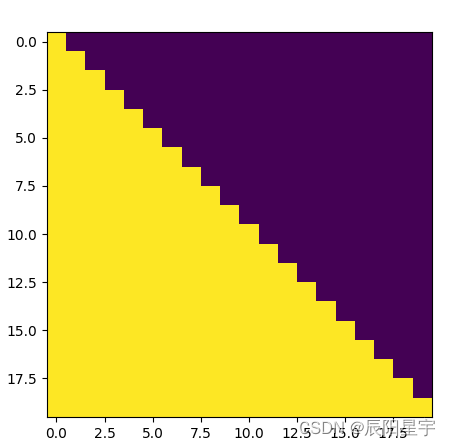
保证目标词汇后面位置的信息被遮掩,不能被看见
(2)Attention注意力机制
引入注意力机制可以计算出到词与词之间的相关程度。
计算规则:
注意力机制需要三个指定的输入Q(query),K(key),V(value),然后通过公式得到注意力的计算结果,这个结果代表queryi在key和value作用下的表示。而这个具体的计算规则有很多种,我这里只介绍我们用到的这一种。
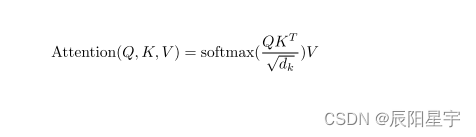
当 Q = K = V 时,为自注意力机制。此时运用注意力机制的时候,相当于是对文本自身进行了一次特征提取。
当 Q != K = V 时,为一般注意力机制。此时运用注意力机制时候,相当于根据查询Q需要的信息,来找到数值V中对应的关键字K。
s o f t m a x ( Q K T d k ) softmax(\frac{QK^T}{\sqrt{d_k}}) softmax(dkQKT) 为经过softmax之后,各个词的注意力得分,和 V V V 相乘后,得到最终的query注意力表示。
注意力机制在网络中实现的图形表示
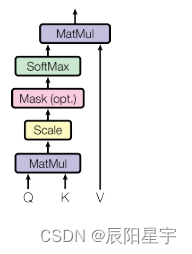
1)先导示例
tensor.masked_fill示例:
# 定义待掩码矩阵
input = torch.rand(5, 5)
print(input)
# 构造需掩码的位置矩阵
mask = torch.zeros(5, 5)
print(mask)
# 将需掩码的位置都替换为-1e9
masked_fill = input.masked_fill(mask==0, -1e9)
print(masked_fill)
# input
tensor([[0.5662, 0.2786, 0.8449, 0.3073, 0.1048],
[0.3237, 0.2584, 0.3089, 0.0409, 0.6550],
[0.2807, 0.6870, 0.2788, 0.4359, 0.0753],
[0.2491, 0.7131, 0.6151, 0.4359, 0.5255],
[0.3250, 0.4919, 0.5008, 0.0894, 0.8480]])
# mask
tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
# masked_fill
tensor([[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09]])
2)attention实现
分为六步走:
(1)得到维度,作为缩放因子d_k
(2)K、Q和d_k相乘,作为关联度分值
(3)判定是否进行掩码操作,让后续内容使用最小值替换,作为掩码覆盖
(4)对关联度分值使用softmax得到p_attn,避免梯度爆炸和梯度消失
(5)判定是否使用dropout,避免过拟合
(6)最后用p_attn和V相乘,得到最终的注意力分值attn
import torch.nn.functional as F
def attention(query, key, value, mask=None, dropout=None):
# 将query的最后一个维度,即对词嵌入维度进行提取
d_k = query.size(-1) # 一般情况下为三维张量 (批个数, 词个数, 词嵌入维度)
# 对key的倒数第一和倒数第二列维度进行互换,再根据注意力公式,进行计算
# Q·K^T/(d_k)^(1/2)
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k) # (批个数, 词个数, 词嵌入维度) * (批个数, 词嵌入维度, 词个数) = (批个数, 词个数, 词个数)
# 判断是否使用掩码张量
if mask is not None:
# 使用tensor的masked_fill方法,掩码scores张量,将scores张量中和掩码张量mask都等于零的位置替换成-1e9,作为最小值
scores = scores.masked_fill(mask==0, -1e9)
# 对scores的最后一个维度上进行softmax操作
p_attn = F.softmax(scores, dim=-1)
# 判定是否使用dropout
if dropout is not None:
p_attn = dropout(p_attn)
# 最后,将p_attn与value张量相乘获得最终的query注意力表示,同时返回注意力张量p_attn
# (批个数, 词个数, 词个数) * (批个数, 词个数, 词嵌入维度) = (批个数, 词个数, 词嵌入维度)
return torch.matmul(p_attn, value), p_attn
示例
自注意力机制示例
无mask掩码方式
## 无mask掩码方式
query = key = value = pe_res
print(query)
attn, p_attn = attention(query, key, value)
print(f"attn: {attn} \n p_attn: {p_attn}")
# query = key = value
tensor([[[-3.2467e+01, -2.7248e+01, -1.2187e+01, ..., -9.8873e+00,
-1.8881e+01, 5.1649e+00],
[ 4.4058e-01, 4.1689e+01, 1.2360e+01, ..., 4.0973e+01,
-9.8002e+00, -1.9118e+01],
[ 3.3154e+01, -3.9283e+01, -3.7957e+01, ..., -1.5100e+01,
-9.5650e+00, 1.8038e+01],
[-2.0440e+01, 6.0866e-03, 2.2342e+01, ..., 3.6270e+00,
-4.1789e+01, -2.2957e+01]],
[[-2.0998e+01, -2.5270e+00, -7.1570e+00, ..., -3.6481e+01,
-8.4572e+00, 7.8671e+00],
[ 3.2288e+01, -6.6180e+00, 5.1974e+01, ..., 1.3861e+01,
-7.2158e+00, -7.2818e+00],
[ 2.8402e+01, -2.8010e+01, -1.3271e+01, ..., 1.1460e+01,
-2.8806e+01, 0.0000e+00],
[ 1.7872e+01, -1.5585e+01, 5.9351e+01, ..., 1.6887e+01,
2.4199e+01, 5.6083e+00]]], grad_fn=<MulBackward0>)
# attn
attn: tensor([[[-3.2467e+01, -2.7248e+01, -1.2187e+01, ..., -9.8873e+00,
-1.8881e+01, 5.1649e+00],
[ 4.4058e-01, 4.1689e+01, 1.2360e+01, ..., 4.0973e+01,
-9.8002e+00, -1.9118e+01],
[ 3.3154e+01, -3.9283e+01, -3.7957e+01, ..., -1.5100e+01,
-9.5650e+00, 1.8038e+01],
[-2.0440e+01, 6.0866e-03, 2.2342e+01, ..., 3.6270e+00,
-4.1789e+01, -2.2957e+01]],
[[-2.0998e+01, -2.5270e+00, -7.1570e+00, ..., -3.6481e+01,
-8.4572e+00, 7.8671e+00],
[ 3.2288e+01, -6.6180e+00, 5.1974e+01, ..., 1.3861e+01,
-7.2158e+00, -7.2818e+00],
[ 2.8402e+01, -2.8010e+01, -1.3271e+01, ..., 1.1460e+01,
-2.8806e+01, 0.0000e+00],
[ 1.7872e+01, -1.5585e+01, 5.9351e+01, ..., 1.6887e+01,
2.4199e+01, 5.6083e+00]]], grad_fn=<UnsafeViewBackward0>)
# p_attn:因采用自注意力非掩码方式,因此第一次attention时候,当然是和自己对应的相关性更强,也就是对角线上的为1,其余的不强,非对角线上为0。
p_attn
p_attn: tensor([[[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]],
[[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]]], grad_fn=<SoftmaxBackward0>)
有mask掩码方式
## 有mask掩码方式
query = key = value = pe_res
print(f"query: {query}")
mask = torch.zeros(2, 4, 4)
attn, p_attn = attention(query, key, value, mask=mask)
print(f"attn: {attn} \n p_attn: {p_attn}")
query: tensor([[[ 7.5491, -0.0000, 3.8558, ..., 0.0000, -0.0000, -0.0000],
[ 15.5168, -14.5373, -3.6362, ..., 1.2756, 9.9690, -24.0013],
[ 4.1040, 0.0000, 36.8071, ..., 5.6728, -37.9900, -6.1248],
[ 22.0409, -13.7412, 50.2689, ..., 29.6889, -19.5435, -10.4330]],
[[-35.2757, -52.6736, -11.3606, ..., -13.7935, 5.6017, -0.0000],
[ 56.3059, -15.9048, -22.7148, ..., -11.7864, 39.4018, 16.7557],
[-42.5410, 33.1815, 20.9338, ..., -17.7185, -0.0000, -18.7593],
[ -0.0000, 19.1597, 68.5530, ..., -10.9749, 35.9611, -24.4019]]],
grad_fn=<MulBackward0>)
attn: tensor([[[ 12.3027, -7.0696, 21.8239, ..., 9.1593, -11.8911, -10.1398],
[ 12.3027, -7.0696, 21.8239, ..., 9.1593, -11.8911, -10.1398],
[ 12.3027, -7.0696, 21.8239, ..., 9.1593, -11.8911, -10.1398],
[ 12.3027, -7.0696, 21.8239, ..., 9.1593, -11.8911, -10.1398]],
[[ -5.3777, -4.0593, 13.8529, ..., -13.5683, 20.2411, -6.6014],
[ -5.3777, -4.0593, 13.8529, ..., -13.5683, 20.2411, -6.6014],
[ -5.3777, -4.0593, 13.8529, ..., -13.5683, 20.2411, -6.6014],
[ -5.3777, -4.0593, 13.8529, ..., -13.5683, 20.2411, -6.6014]]],
grad_fn=<UnsafeViewBackward0>)
p_attn: tensor([[[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500]],
[[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500]]], grad_fn=<SoftmaxBackward0>)
(3)Multi-Attention多头注意力机制
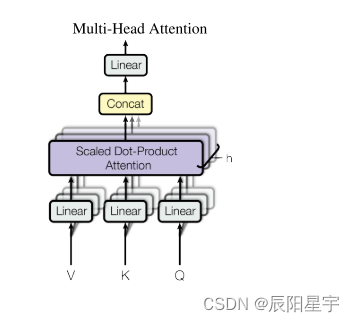
为了可以识别不一样的模式,便让Q、K、V投影到低维,将词嵌入维度进行分块切割,使用一组线性变化层,使用三个变换张量对Q、K、V分别进行线性变换,这些变换不改变原有张量的尺寸,因此每个变换矩阵都是方阵。进行h次点积计算注意力,最后获取到不一样的模式关系,不一样的相似函数。类似于多输出通道。
作用:
这种结构的设计能让每个注意力机制去优化每个词汇的不同特征部分,从而均衡同一种注意力机制可能产生的偏差,让词义拥有来自更多元的表达。实验表明这种方式,可以提升模型效果。

其中,Q、K、V会经过一个全连接层,使用随机初始化权重w和偏置b,对其进行一个线性变换。
1)先导示例
tensor.view
一个用于改变张量形状的函数。它允许以不同的维度重新塑造一个张量,而不会改变其元素,只改变了数据的视图。
x = torch.randn(4, 4)
print(x.size())
y = x.view(16)
print(y.size())
z = x.view(-1, 8)
print(z)
# x.size()
torch.Size([4, 4])
# y.size()
torch.Size([16])
# z
tensor([[ 0.8721, 1.5081, -0.7396, -1.7734, 1.0451, -0.3674, 1.4778, -0.4577],
[-1.4658, -2.8492, 0.0093, -0.2415, -1.1663, 1.9635, -1.1655, 0.6022]])
a = torch.randn(1, 2, 3, 4)
print(a.size())
b = a.transpose(1, 2)
print(b.size())
print(b)
c = a.view(1, -1, 2, 2) # -1 让其自适应
print(c.size())
print(torch.equal(b, c))
# a.size()
torch.Size([1, 2, 3, 4])
# b.size()
torch.Size([1, 3, 2, 4])
# b
tensor([[[[-0.8545, 1.2432, -1.2231, -1.5342],
[-1.2262, -0.3905, 0.3301, -0.0680]],
[[-0.7892, 0.2163, 1.7285, 0.2881],
[ 0.3259, 1.2389, 1.2471, -1.3347]],
[[ 0.0696, 0.3491, -0.6072, 0.8423],
[-0.9106, -1.8367, 0.6080, 0.8363]]]])
# c.size()
torch.Size([1, 6, 2, 2])
# torch.equal(b, c)
False
nn.Linear(input_dim, output_dim, bias=True)
定义了一个全连接层: Y = X W + b Y = XW+b Y=XW+b,其中W和b会随机初始化。
参考文章:Pytorch nn.Linear的基本用法与原理详解
2)MultiHeadedAttention多头注意力机制实现
主要分为六步:
(1)设置准备参数:
1)判定词嵌入维度和注意力头数能否被整除
2)获取每个头的词嵌入维度、获取注意力头数h
3)构建四个实例化线性层、定义注意力张量、设置dropout层
(2)扩充掩码第一维度作为头数、获取批数
(3)将QKV进行线性变换,然后再分割出h个注意力头
(4)对h个头使用注意力机制
(5)合并头,还原维度
(6)对合并后的头进行线性变换
# 克隆函数:因为在多头注意力机制下,需要用到多个结构相同的线性层,直接用clones函数克隆即可,放置网络层列表对象中,不需要再重新多次定义
def clones(module, N):
# module:要克隆的目标网络层、N:将module克隆的个数
# copy.deepcopy(module)会创建module模块的一个完全独立的副本
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
# 多头注意力机制
class MultiHeadedAttention(nn.Module):
'''
在类的初始化时,会传入三个参数:
head:注意力头数
embedding_dim:词嵌入维度
dropout:置0比率
'''
def __init__(self, head, embedding_dim, dropout=0.1):
super(MultiHeadedAttention, self).__init__()
# 使用assert语句,判定词嵌入维度d_model能否被注意力头数head整除,保证每个头分配等量的词特征
assert embedding_dim % head == 0
# 对每个注意力头进行分割,d_k为降维后的词嵌入维度
self.d_k = embedding_dim // head
# 传入注意力头数
self.head = head
# 拷贝线性层对象,通过nn的Linear实例化,实例化了四个对象,分别为Q、K、V和最后一个拼接输出层
self.linears = clones(nn.Linear(embedding_dim, embedding_dim), 4)
# 定义self.attn代表最后得到的注意力张量
self.attn = None
# 设置dropout层
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
'''
:param query:
:param key:
:param value:
:param mask:
:return:
'''
if mask is not None:
# 使用squeeze将掩码张量进行维度扩充,扩充第一维度,第一维度为多头注意力中的第几个头
mask = mask.unsqueeze(1)
# 得到批数
batch_size = query.size(0)
# 将QKV进行线性变换并分割出多个头
# (1)使用zip将QKV与三个线性层组到一起,然后使用for循环,将输入QKV分别传到线性层中,进行线性变换
# (2)将d_model拆分为了两部分:head头数和d_k每个头里的词嵌入维度,为每个头分割词嵌入维度,使用view方法对线性变换的结果进行维度重塑
# (3)第一维度为词汇长度,交换第一维和第二维,让句子长度和词嵌入维度靠近,便于注意力机制找到词义与句子位置之间的关系,提高计算效率
# 此时变为(批数, 头, 词个数, 词嵌入维度)
query, key, value = \
[model(x).view(batch_size, -1, self.head, self.d_k).transpose(1, 2)
for model, x in zip(self.linears, (query, key, value))] # 此时只用了三个线性层
# 对各个分割后的QKV使用注意力机制
x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout)
# 合并升维,汇聚出最终的注意力表示,此时形状为 (批数, 词个数, 词嵌入维度)
# (1)重新交换第一维度和第二维度,进行还原
# (2)使用contiguous()可以让不连续的张量进行view操作
# (3)将分割后的头得到个各个注意力表示合并,还原维度
x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.head * self.d_k)
# 使用线性层列表中的最后一个线性层对输入进行线性变换得到最终的多头注意力结构的输出
return self.linears[-1](x)
示例
# MultiHeadedAttetion示例
head = 8
embedding_dim = 512
dropout = 0.2
# 使用自注意力
query = key = value = pe_res
print("pe_res:",pe_res)
mask = torch.zeros(2, 4, 4)
mha = MultiHeadedAttention(head, embedding_dim, dropout)
mha_res = mha(query, key, value, mask)
print(f"mha_res: {mha_res}, \n shape:{mha_res.shape}")
# 注意力机制前的张量
pe_res: tensor([[[ 4.3315, -29.6712, -11.4785, ..., 24.2612, -42.0858, 17.0310],
[-24.5543, -18.9879, -28.9953, ..., 2.6159, -19.8559, -4.3193],
[-52.5631, -0.0000, 2.7141, ..., -31.9027, 11.8139, 0.0000],
[ 12.5088, -29.1743, -6.1350, ..., -15.9323, 4.6862, 0.0000]],
[[ 1.7454, 15.3640, -18.5756, ..., -49.9147, 21.6549, 11.1382],
[-19.5803, -11.6190, 15.7270, ..., -1.4723, 14.6670, 42.7504],
[-22.9932, 16.9854, 31.3982, ..., 2.9833, 31.3632, -0.2333],
[ 16.5026, -64.2235, 7.7251, ..., -31.2948, -2.5888, -17.0270]]],
grad_fn=<MulBackward0>)
# 注意力机制后的张量
mha_res: tensor([[[ 2.9608, 6.7184, 1.6315, ..., -2.4122, 6.0816, 4.8318],
[ 5.5282, 6.9530, 2.2891, ..., -2.4104, 1.8758, 6.9588],
[ 7.2244, 6.8778, 2.4657, ..., -4.6782, 3.2852, 4.0077],
[ 3.6417, -2.0250, -0.2807, ..., -0.2300, 5.9994, 1.0701]],
[[-2.5653, -1.8093, -0.9984, ..., 3.5322, -2.1962, -7.5779],
[-1.7946, -1.6483, -1.9993, ..., 3.0050, 0.3547, -6.7668],
[-1.6770, -3.2119, -4.7261, ..., 5.4974, -2.7692, -6.9897],
[-2.5106, -0.8810, -0.4256, ..., 1.5076, -1.6359, -5.1002]]],
grad_fn=<ViewBackward0>),
shape:torch.Size([2, 4, 512])
和下方单头注意力机制进行对比,可发现上方多头注意力机制,表示更加丰富。
attn: tensor([[[ 12.3027, -7.0696, 21.8239, ..., 9.1593, -11.8911, -10.1398],
[ 12.3027, -7.0696, 21.8239, ..., 9.1593, -11.8911, -10.1398],
[ 12.3027, -7.0696, 21.8239, ..., 9.1593, -11.8911, -10.1398],
[ 12.3027, -7.0696, 21.8239, ..., 9.1593, -11.8911, -10.1398]],
[[ -5.3777, -4.0593, 13.8529, ..., -13.5683, 20.2411, -6.6014],
[ -5.3777, -4.0593, 13.8529, ..., -13.5683, 20.2411, -6.6014],
[ -5.3777, -4.0593, 13.8529, ..., -13.5683, 20.2411, -6.6014],
[ -5.3777, -4.0593, 13.8529, ..., -13.5683, 20.2411, -6.6014]]],
grad_fn=<UnsafeViewBackward0>)
注意:将QKV先进行一个线性变换的原因:
在多头注意力机制中,将查询、键和值进行线性变换的目的是为了引入额外的参数和变换,以增强模型的表征能力和灵活性。通过为每个注意力头引入独立的线性变换,可以使得每个头学习不同的特征表示。不同的线性变换矩阵会使得每个注意力头关注不同的信息和特征,从而增加了模型的多样性和灵活性。
拓展阅读:【Transformer系列(2)】注意力机制、自注意力机制、多头注意力机制、通道注意力机制、空间注意力机制超详细讲解
(3)前馈全连接层
前馈全连接层是具有两层线性层的全连接网络,因为注意力机制可能对复杂过程的拟合程度不够,因此通过增加两层网络来增强模型的拟合能力。
class PositionwiseFeedForward(nn.Module):
'''
d_model: 词嵌入维度
d_ff: 第一个线性层的输出维度和第二个线性层的输入维度
dropout: 随机置零比率
'''
def __init__(self, d_model, d_ff, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
# 定义两层全连接的线性层
self.w1 = nn.Linear(d_model, d_ff)
self.w2 = nn.Linear(d_ff, d_model)
self.dropout = nn.Dropout(p=dropout)
def forward(self, x):
'''先经过一个线性层,再使用relu函数进行激活处理,再经过dropout让其部分失活,最后再进入第二个线性层输出
:param x: 来自上一个线性层的输出
:return: 经过两个线性层的线性变化
'''
return self.w2(self.dropout(F.relu(self.w1(x))))
示例
d_model = 512
d_ff = 64
dropout = 0.2
x = mha_res
print(f"x: {x}")
ff = PositionwiseFeedForward(d_model, d_ff, dropout)
ff_res = ff(x)
print(f"ff_res: {ff_res}\n shape:{ff_res.shape}")
x: tensor([[[ 2.1565, -1.8590, 2.8168, ..., -1.2693, 1.8211, 3.3622],
[ 0.9119, 0.8808, -0.2330, ..., -5.0184, 3.1404, 3.5138],
[ 4.3088, -1.1293, 1.0864, ..., -5.2556, 1.8978, 7.2585],
[ 2.6184, -3.0563, 0.5501, ..., -6.8723, 2.3841, 6.4860]],
[[-1.0458, -5.2068, -8.9496, ..., -3.8729, -7.9293, 7.2939],
[ 0.5122, -4.4917, -8.1726, ..., -5.8970, -5.1041, 4.4758],
[ 2.0483, -9.1332, -9.6163, ..., -4.0692, -7.8080, 7.1726],
[ 5.5644, -9.4695, -8.8962, ..., -6.0035, -6.1042, 4.0922]]],
grad_fn=<ViewBackward0>)
ff_res: tensor([[[ 0.2238, 3.5273, 1.0154, ..., -1.5940, 0.4424, -1.5687],
[-0.5018, 3.3703, -0.5249, ..., -1.9299, 0.4065, -2.8288],
[-0.3591, 3.8767, 1.3923, ..., -1.8782, 0.3630, -2.2941],
[-1.3599, 3.7256, 0.6494, ..., -1.5400, 0.1696, -2.2202]],
[[-0.4818, 1.1380, -1.2246, ..., 0.3083, 0.4064, 0.2124],
[-1.7425, -1.1619, -1.5198, ..., -0.8393, 0.8195, 0.8223],
[-0.3670, -0.5432, 1.4519, ..., 0.2707, 0.6893, 0.1386],
[-0.0691, -0.9774, -0.9932, ..., -0.3170, 1.6495, -0.8146]]],
grad_fn=<ViewBackward0>)
shape:torch.Size([2, 4, 512])
(4)规范化层
规范化层是所有深层网络模型都需要的标准网络,因为随着网络层数的增加,经多层计算后参数可能会变的过大或过小,从而导致学习过程出现异常,模型可能收敛非常的慢。因此,都会在一定层数后加入一个规范化层进行数值规范化操作,使其特征数值在一个合理的范围内。

class LayerNorm(nn.Module):
def __init__(self, features, eps=1e-6):
'''
:param fetures:词嵌入维度
:param eps: 防止分母为0,添加一个非常小的数
'''
# 根据features的形状初始化两个参数张量a2和b2,第一个初始化为1张量,第二个初始化为0张量,这两个张量就是规范化层的参数。
# 若直接对上一层得到的结果做规范化公式计算,将改变结果的正常表征,因此需要有参数作为调节因子。
# 使用nn.Parameter进行封装代表是模型的参数。
super(LayerNorm, self).__init__()
self.a2 = nn.Parameter(torch.ones(features))
self.b2 = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
''' 使用标准化公式处理
:param x: 来自上一层的输出
:return: 规范化后的张量
'''
mean = x.mean(-1, keepdim=True) # 对输入变量x求最后一个维度的均值,并保持输出维度与输入维度一致
std = x.std(-1, keepdim=True) # 再求标准差
# 使用规范化公式在分母位置加上了一个eps防止分母为0,最后对结果乘以方所参数即a2
return self.a2 * (x - mean) / (std + self.eps) + self.b2
示例
features = d_model = 512
eps = 1e-6
x = ff_res
ln = LayerNorm(features, eps)
ln_res = ln(x)
print(f"ln_res: {ln_res}\n shape: {ln_res.shape}")
ln_res: tensor([[[-0.1765, 0.6963, 0.1440, ..., 1.0402, 0.8889, -0.6844],
[-0.0178, 0.1931, -0.3235, ..., 0.8976, 0.9551, 0.3127],
[ 1.0035, 0.8750, -0.6121, ..., 0.2702, 0.5427, -0.5236],
[-0.2309, 0.1464, 0.4505, ..., -0.8241, 0.4977, 1.2293]],
[[ 0.7723, -0.3876, -0.0118, ..., -0.0469, 0.1177, -0.6833],
[-0.2411, -1.6828, -0.5819, ..., 0.0319, -0.1524, -0.5997],
[-0.3922, -1.1382, -0.8326, ..., 0.4178, 1.3486, 0.4128],
[-1.1679, -0.7673, -0.5074, ..., 0.2883, 0.6682, 0.5297]]],
grad_fn=<AddBackward0>)
shape: torch.Size([2, 4, 512])
和下述规范化前的进行对比
ff_res: tensor([[[-0.1495, 0.5323, 0.1009, ..., 0.8011, 0.6829, -0.5463],
[-0.0670, 0.1551, -0.3890, ..., 0.8971, 0.9576, 0.2810],
[ 0.9664, 0.8344, -0.6934, ..., 0.2131, 0.4930, -0.6025],
[-0.2149, 0.0911, 0.3377, ..., -0.6960, 0.3760, 0.9693]],
[[ 0.9420, -0.4847, -0.0224, ..., -0.0656, 0.1368, -0.8484],
[-0.2766, -1.9478, -0.6716, ..., 0.0399, -0.1737, -0.6922],
[-0.4119, -1.2546, -0.9094, ..., 0.5032, 1.5547, 0.4976],
[-1.0953, -0.7267, -0.4875, ..., 0.2445, 0.5941, 0.4667]]],
grad_fn=<ViewBackward0>)
引入a2和b2的目的:
通过引入可学习的参数 self.a2 和 self.b2,模型可以自适应地学习数据的缩放和平移,以更好地适应不同的数据分布和任务要求。这种可学习的缩放和平移操作可以增加模型的灵活性和表征能力,使得模型能够更好地拟合训练数据,并具有更好的泛化能力。
(5)子层连接结构
实现残差连接,随着网络层数加深的时候,可以缓解梯度消失。
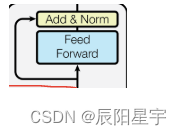
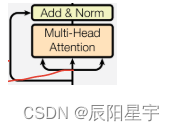
在编码器里有两个子层,解码器里有三个子层。
class SublayerConnection(nn.Module):
def __init__(self, size, dropout=0.1):
"""
将规范化层和Dropout层放到结构里
:param size: 词嵌入维度大小
:param dropout: 置0比率
"""
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(p=dropout)
def forward(self, x, sublayer):
"""
对x进行规范化,然后将结果传给子层处理,之后再进行dropout操作
:param x: 上一层传入的张量
:param sublayer: 子层连接中子层函数
:return: 残差连接
"""
return x + self.dropout(sublayer(self.norm(x)))
示例
size = d_model = 512
head = 8
dropout = 0.2
## 构建子层
x = pe_res # 令x为位置编码器后的输出
mask = torch.zeros(2, 4, 4)
self_attn = MultiHeadedAttention(head, d_model)
sublayer = lambda x: self_attn(x, x, x, mask) # 使用lambda获得一个函数类型的子层,此时K=Q=V=x
## 调用子层连接
sc = SublayerConnection(size, dropout)
sc_res = sc(x, sublayer)
print(f"sc_res: {sc_res}\n shape: {sc_res.shape}")
sc_res: tensor([[[ 1.1769e+01, 1.5094e+01, -1.1459e+01, ..., -2.0053e+01,
3.5621e+01, -2.6102e+00],
[ 8.4440e-01, 5.6780e+01, -3.2259e+01, ..., -4.9596e+01, -1.2592e+01, -1.0750e+01],
[ 3.7462e+01, 4.8253e+00, 3.9283e+01, ..., -8.8898e+00, -1.8832e+00, 2.3375e+01],
[-3.5279e+00, -1.8733e+01, -3.6783e-02, ..., -3.6409e+00, 2.0954e+01, 4.2237e+00]],
[[ 7.1081e+00, 2.6611e+01, 1.1299e+01, ..., 1.4271e+01, 1.2571e+01, 3.8807e-01],
[ 2.3168e+01, 5.3653e+00, -3.1167e+01, ..., 4.1468e+01, -1.8078e+01, -5.0934e+00],
[-6.8489e+00, 1.3600e+01, 2.2246e+01, ..., 1.0667e+01, 0.0000e+00, 1.6812e+01],
[ 3.8327e+01, -7.8942e+00, -6.0824e+00, ..., -6.1427e+00, -4.5801e+01, -2.4354e+01]]], grad_fn=<AddBackward0>)
shape: torch.Size([2, 4, 512])
和下面没有调用子层连接,只经过规范化层输出进行对比
ln_res: tensor([[[ 0.5942, -1.0976, -1.4083, ..., -1.5857, -0.4352, -1.8763],
[ 0.0387, -1.5223, -1.3550, ..., -1.9196, -0.5209, -0.7036],
[-0.1905, -1.0026, -1.8450, ..., -2.4262, -0.2016, -0.9960],
[ 0.3860, -0.8752, -2.1516, ..., -1.2487, 0.2503, -1.4723]],
[[ 0.0178, -0.3065, -2.4651, ..., -0.6820, 2.1495, -1.0772],
[-2.2911, -0.5655, -2.4541, ..., 0.2550, 2.7482, -1.4490],
[-0.5257, -0.0802, -1.2602, ..., 1.0214, 2.3603, -1.0336],
[ 0.2162, 0.8301, -1.6483, ..., 0.4591, 0.7930, 0.0767]]],
grad_fn=<AddBackward0>)
shape: torch.Size([2, 4, 512])