【数据结构】树与二叉树（六）：二叉树的链式存储

文章目录

5.1 树的基本概念
- 5.1.1 树的定义
- 5.1.2 森林的定义
- 5.1.3 树的术语
- 5.1.4 树的表示
5.2 二叉树
- 5.2.1 二叉树
- - 1. 定义
  - 2. 特点
  - 3. 性质
  - 4. 满二叉树
  - 5. 完全二叉树
- 5.2.2 二叉树顺序存储
- 5.2.3 二叉树链接存储
- - C语言实现

5.1 树的基本概念

5.1.1 树的定义

一棵树是结点的有限集合T：
- 若T非空，则：
  - 有一个特别标出的结点，称作该树的根，记为root(T)；
  - 其余结点分成若干个不相交的非空集合T1, T2, …, Tm (m>0)，其中T1, T2, …, Tm又都是树，称作root(T)的子树。
- T 空时为空树，记作root(T)=NULL。

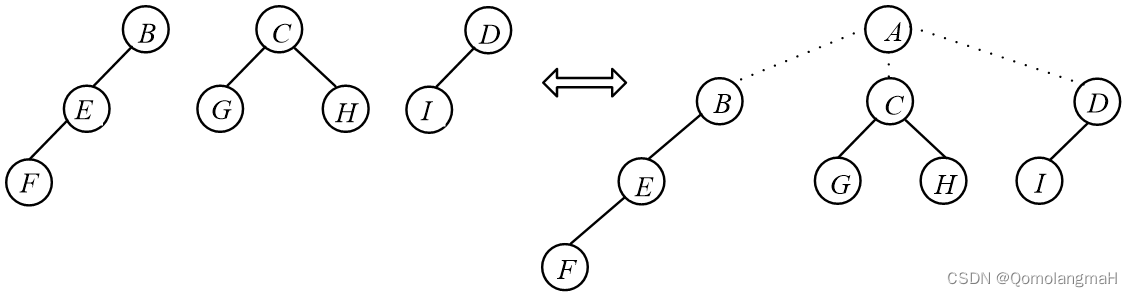
5.1.2 森林的定义

一个森林是0棵或多棵不相交（非空）树的集合，通常是一个有序的集合。换句话说，森林由多个树组成，这些树之间没有交集，且可以按照一定的次序排列。在森林中，每棵树都是独立的，具有根节点和子树，树与树之间没有直接的连接关系。
森林是树的扩展概念，它是由多个树组成的集合。在计算机科学中，森林也被广泛应用于数据结构和算法设计中，特别是在图论和网络分析等领域。
在这里插入图片描述

5.1.3 树的术语

父亲（parent）、儿子（child）、兄弟（sibling）、后裔（descendant）、祖先（ancestor）
度（degree）、叶子节点（leaf node）、分支节点（internal node）
结点的层数
路径、路径长度、结点的深度、树的深度

参照前文：【数据结构】树与二叉树（一）：树（森林）的基本概念：父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度

5.1.4 树的表示

【数据结构】树与二叉树（二）：树的表示C语言：树形表示法、嵌套集合表示法、嵌套括号表示法、凹入表示法

5.2 二叉树

5.2.1 二叉树

1. 定义

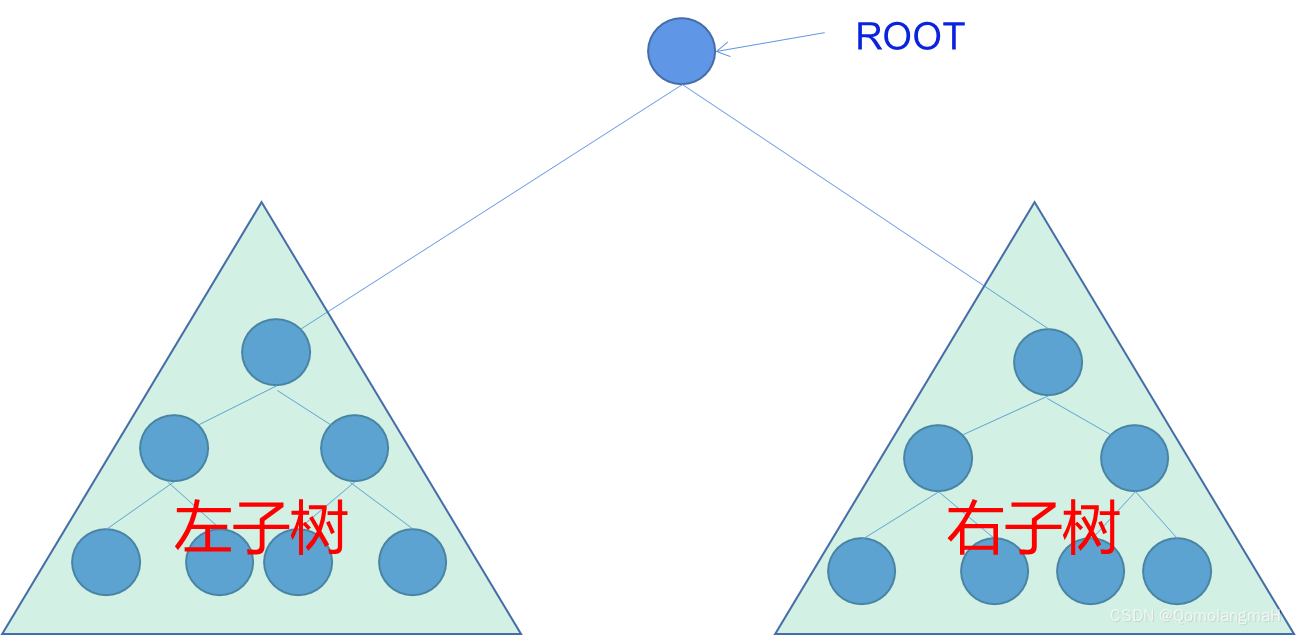
二叉树是一种常见的树状数据结构，它由结点的有限集合组成。一个二叉树要么是空集，被称为空二叉树，要么由一个根结点和两棵不相交的子树组成，分别称为左子树和右子树。每个结点最多有两个子结点，分别称为左子结点和右子结点。
在这里插入图片描述

2. 特点

二叉树的特点是每个结点最多有两个子结点，并且子结点的位置是有序的，即左子结点在前，右子结点在后。这种有序性使得二叉树在搜索、排序等算法中有广泛的应用。

在二叉树中，根结点是整个树的起始点，通过根结点可以访问到整个树的其他结点。每个结点都可以看作是一个独立的二叉树，它的左子树和右子树也是二叉树。
二叉树可以是空树，也可以是只有根结点的树，或者是由多个结点组成的树。每个结点可以包含一个数据元素，以及指向左子结点和右子结点的指针。
二叉树的形状可以各不相同，它可以是平衡的或者不平衡的，具体取决于结点的分布情况。在二叉树中，每个结点的左子树和右子树都是二叉树，因此可以通过递归的方式来处理二叉树的操作。

3. 性质

引理5.1：二叉树中层数为i的结点至多有 $2^i$ 个，其中 $\geq 0$ 。

引理5.2：高度为k的二叉树中至多有 $2^{k+1}-1$ 个结点，其中 $\geq 0$ 。

引理5.3：设T是由n个结点构成的二叉树，其中叶结点个数为 $n_0$ ，度数为2的结点个数为 $n_2$ ，则有 $n_0 = n_2 + 1$ 。

详细证明过程见前文：【数据结构】树与二叉树（三）：二叉树的定义、特点、性质及相关证明

4. 满二叉树

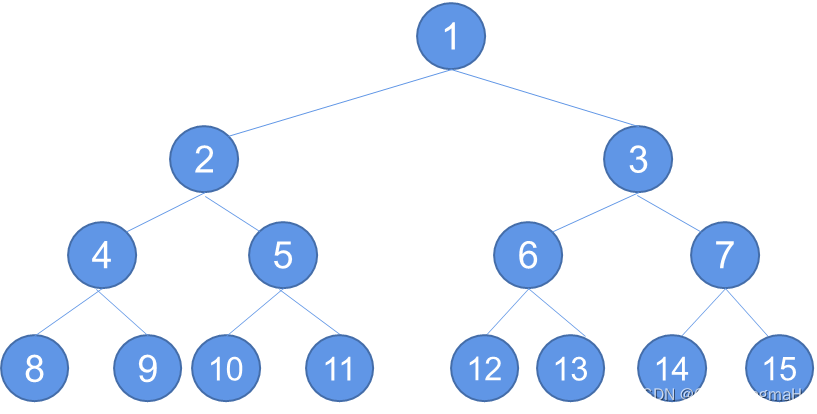
在这里插入图片描述

定义5.3：一棵非空高度为 $k (k \geq 0)$ 的满二叉树(perfect binary tree)，是有 $2^{k+1}-1$ 个结点的二叉树。

5. 完全二叉树

定义5.4：一棵包含 $n$ 个节点、高度为 $k$ 的二叉树 $T$ ，当按层次顺序编号 $T$ 的所有节点，对应于一棵高度为 $k$ 的满二叉树中编号由1至 $n$ 的那些节点时， $T$ 被称为完全二叉树（complete binary tree）。

满二叉树、完全二叉树性质及证明：【数据结构】树与二叉树（四）：满二叉树、完全二叉树及其性质

5.2.2 二叉树顺序存储

二叉树的顺序存储是指将二叉树中所有结点按层次顺序存放在一块地址连续的存储空间中，详见：
【数据结构】树与二叉树（五）：二叉树的顺序存储（初始化，插入结点，获取父节点、左右子节点等）

顺序存储方式的优点是节省了存储空间，同时访问结点也非常快速，因为可以通过数组索引直接访问结点，而不需要进行指针的跳转。然而，顺序存储方式也有一些限制：

空间浪费：对于非完全二叉树，顺序存储方式可能会浪费大量存储空间。因为顺序存储方式需要使用连续的存储空间来存储所有结点，而非完全二叉树中存在许多空缺的位置，这些位置将被浪费掉。
动态性差：顺序存储方式需要提前确定二叉树的最大结点个数，对于结点数不确定或者动态变化的情况下，顺序存储方式不太适用。如果二叉树的结点数超过了预先分配的存储空间，就需要重新分配更大的存储空间并进行数据迁移，这会增加额外的开销。
插入和删除操作复杂：对于顺序存储方式，插入和删除操作比较复杂。当需要插入或删除一个结点时，需要进行数据的移动和调整，以保持完全二叉树的性质。这会导致较高的时间复杂度和额外的操作开销。

因此，对于非完全二叉树或者需要频繁进行插入和删除操作的情况，链式存储方式更为灵活和高效。

5.2.3 二叉树链接存储

二叉树的链接存储系指二叉树诸结点被随机存放在内存空间中，结点之间的关系用指针说明。在链式存储中，每个二叉树结点都包含三个域：数据域（Data）、左指针域（Left）和右指针域（Right），用于存储结点的信息和指向子结点的指针。具体结点的结构如下所示：

struct BinaryTreeNode {
    DataType Data;  // 数据域，存放结点的信息
    BinaryTreeNode* Left;  // 左指针域，指向左子结点
    BinaryTreeNode* Right;  // 右指针域，指向右子结点
};

每个结点通过指针域与其左子结点和右子结点建立联系，形成二叉树的结构。通过这种链接方式，可以方便地遍历和操作二叉树。
链式存储方式的优点是灵活性高，适用于各种类型的二叉树，无需提前确定结点个数，适用于动态变化的情况。同时，链式存储方式不要求连续的存储空间，每个结点可以在内存中的任意位置，通过指针的连接来表示结点之间的逻辑关系。
然而，链式存储方式也存在一些缺点。相比于顺序存储方式，链式存储需要额外的指针开销，每个结点都需要额外的指针域来存储指向子结点的指针。此外，访问结点需要通过指针的跳转，相对于顺序存储方式来说，可能会稍微降低访问效率。

在二叉树的链接存储中，存在一个指向根结点的指针，通常称为根指针。根指针用于访问整个二叉树。如果二叉树为空，根指针将被设置为NULL（即空指针）。
叶结点是没有子结点的结点，因此叶结点的左指针域和右指针域都会存放NULL，表示没有左子结点和右子结点。
在包含n个结点的二叉树的链接存储中，需要2n个指针域。其中，n-1个指针域用于指示结点的左子结点和右子结点，剩余的n+1个指针域为空。这是因为树中的每个结点（除了根结点）都有一个父结点，而父结点与子结点之间有两个指针域（左指针域和右指针域）相连，所以总共需要2n个指针域。但是根结点没有父结点，因此只有n-1个指针域用于指示结点的左子结点和右子结点。这个结论可以通过引理5.3（E = n-1）**来证明。

C语言实现

#include <stdio.h>
#include <stdlib.h>

// 二叉树的节点结构
typedef struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
} TreeNode;

// 创建新节点
TreeNode* createNode(int value) {
    TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
    node->data = value;
    node->left = NULL;
    node->right = NULL;
    return node;
}

// 向二叉树中插入节点
void insertNode(TreeNode** root, int value) {
    if (*root == NULL) {
        *root = createNode(value);
        return;
    }

    if (value < (*root)->data) {
        insertNode(&((*root)->left), value);
    } else {
        insertNode(&((*root)->right), value);
    }
}

// 前序遍历二叉树
void preorderTraversal(TreeNode* root) {
    if (root == NULL) {
        return;
    }

    printf("%d ", root->data);
    preorderTraversal(root->left);
    preorderTraversal(root->right);
}

int main() {
    TreeNode* root = NULL;

    // 向二叉树中插入节点
    insertNode(&root, 4);
    insertNode(&root, 2);
    insertNode(&root, 6);
    insertNode(&root, 1);
    insertNode(&root, 3);
    insertNode(&root, 5);
    insertNode(&root, 7);

    // 前序遍历二叉树
    printf("Preorder traversal: ");
    preorderTraversal(root);
    printf("\n");

    return 0;
}