常见的降维方法有主成分分析、 线性判别分析、 等距映射、 局部线性嵌入、 拉普拉斯特征映射、 局部保留投影等。
1 PCA最大方差角度理解
PCA无监督学习算法。
PCA的目标, 即最大化投影方差, 也就是让数据在主轴上投影的方差最大。
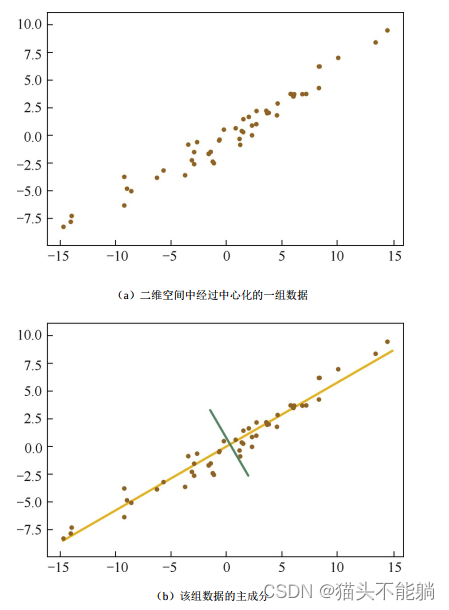
在黄线所处的轴上, 数据分布得更为分散, 这也意味着数据在这个方向上方差更大。 在信号处理领域, 我们认为信号具有较大方差, 噪声具有较小方差, 信号与噪声之比称为信噪比。 信噪比越大意味着数据的质量越好。


其实就是样本协方差矩阵,我们将其写作Σ,由于ω是单位方向向量, 即有ωTω=1。要求解投影后方差最大化问题, 可表示为:
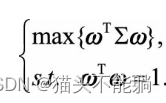
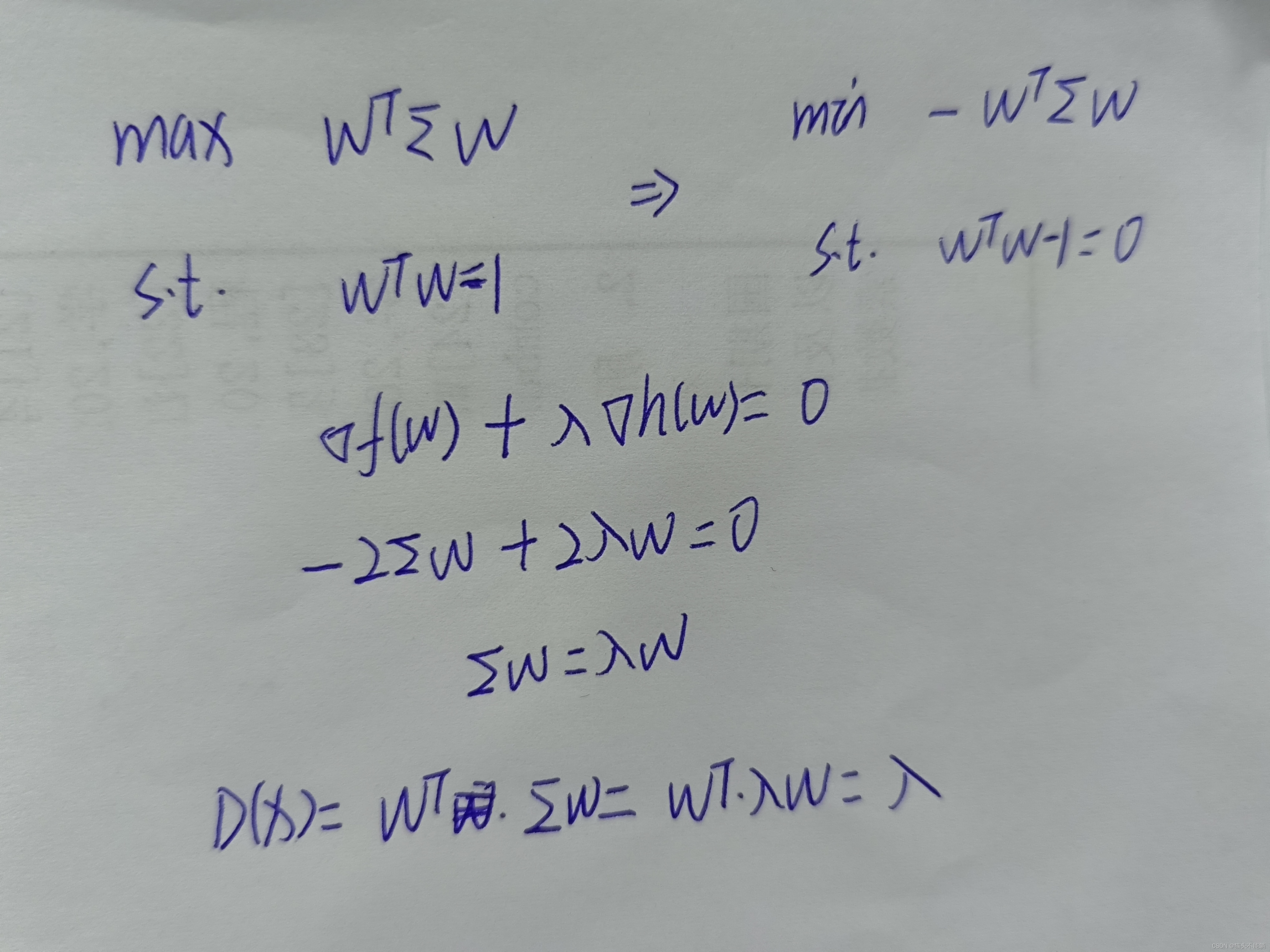 x投影后的方差就是协方差矩阵的特征值。 我们要找到最大的方差也就是协方差矩阵最大的特征值, 最佳投影方向就是最大特征值所对应的特征向量。 得到以下PCA的求解方法:
x投影后的方差就是协方差矩阵的特征值。 我们要找到最大的方差也就是协方差矩阵最大的特征值, 最佳投影方向就是最大特征值所对应的特征向量。 得到以下PCA的求解方法:
( 1) 对样本数据进行中心化处理。
( 2) 求样本协方差矩阵。
( 3) 对协方差矩阵进行特征值分解, 将特征值从大到小排列。
( 4) 取特征值前d大对应的特征向量ω1,ω2,…,ωd, 通过以下映射将n维样本映
射到d维:
 新的xi′的第d维就是xi在第d个主成分ωd方向上的投影, 通过选取最大的d个特征值对应的特征向量, 我们将方差较小的特征( 噪声) 抛弃, 使得每个n维列向量xi被映射为d维列向量xi′, 定义降维后的信息占比为:
新的xi′的第d维就是xi在第d个主成分ωd方向上的投影, 通过选取最大的d个特征值对应的特征向量, 我们将方差较小的特征( 噪声) 抛弃, 使得每个n维列向量xi被映射为d维列向量xi′, 定义降维后的信息占比为:

2 PCA最小平方误差角度理解
从求解直线的思路出发, 很容易联想到数学中的线性回归问题, 其目标也是求解一个线性函数使得对应直线能够更好地拟合样本点集合。 如果我们从这个角度定义PCA的目标, 那么问题就会转化为一个回归问题。即把样本点投影到最佳直线, 最小化的就是所有点到直线的距离平方之和。
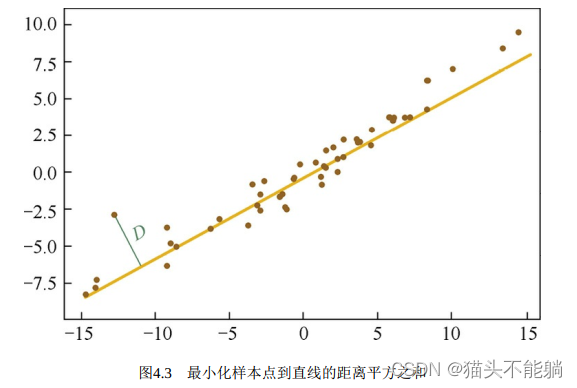
PCA要优化的目标为:

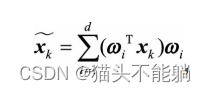
进行推导:

因此原来的式子可以表示为:

这等价于求解带约束的优化问题:
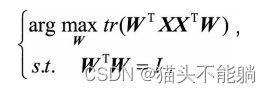
如果我们对W中的d个基 依次求解, 就会发现和最大方差理论的方法完全等价。 比如当d=1时, 我们实际求解的问题是:
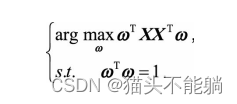
最佳直线ω与最大方差法求解的最佳投影方向一致, 即协方差矩阵的最大特征值所对应的特征向量, 差别仅是协方差矩阵Σ的一个倍数, 以及常数.但这并不影响我们对最大值的优化。
3 线性判别分析LDA
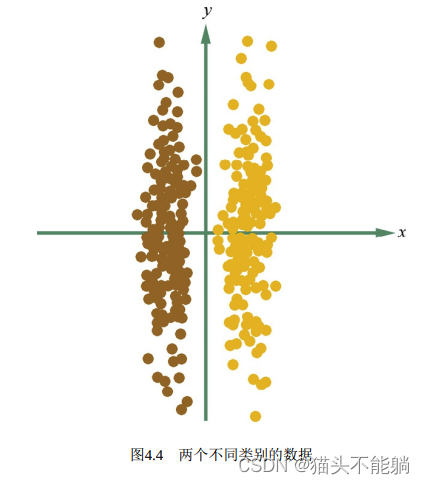
LDA有监督学习算法。最大化类间距离、 最小化类内距离。
在PCA中, 算法没有考虑数据的标签(类别) , 只是把原数据映射到一些方差比较大的方向上而已。
 从这里我们可以看出, 我们最大化的目标对应了一个矩阵的特征值, 于是LDA降维变成了一个求矩阵特征向量的问题。 J(ω)就对应了矩阵 Sw−1SB最大的特征值, 而投影方向就是这个特征值对应的特征向量。换句话说, 我们只需要求样本的均值和类内方差, 就可以马上得出最佳的投影方向ω。
从这里我们可以看出, 我们最大化的目标对应了一个矩阵的特征值, 于是LDA降维变成了一个求矩阵特征向量的问题。 J(ω)就对应了矩阵 Sw−1SB最大的特征值, 而投影方向就是这个特征值对应的特征向量。换句话说, 我们只需要求样本的均值和类内方差, 就可以马上得出最佳的投影方向ω。
4LDA和PCA区别与联系
从目标出发, PCA选择的是投影后数据方差最大的方向。 由于它是无监督的, 因此PCA假设方差越大, 信息量越多, 用主成分来表示原始数据可以去除冗余的维度, 达到降维。 而LDA选择的是投影后类内方差小、 类间方差大的方向。 其用到了类别标签信息, 为了找到数据中具有判别性的维度, 使得原始数据在这些方向上投影后, 不同类别尽可能区分开。