0.1+0.2为什么不等于0.3

news2024/12/23 15:40:56

在这里插入图片描述

一、0.1+0.2是如何执行的？

1、转成浮点数

浮点数在计算机内部是以二进制的形式存储的，而有些十进制的小数在二进制下无法精确表示，因此在进行浮点数运算时可能会存在精度误差。

浮点数分为单精度对应32位操作系统和双精度对应64位操作系统。目前的操作系统大多是64位操作系统，故这里只解释一下二进制如何转成双精度浮点数的二进制。

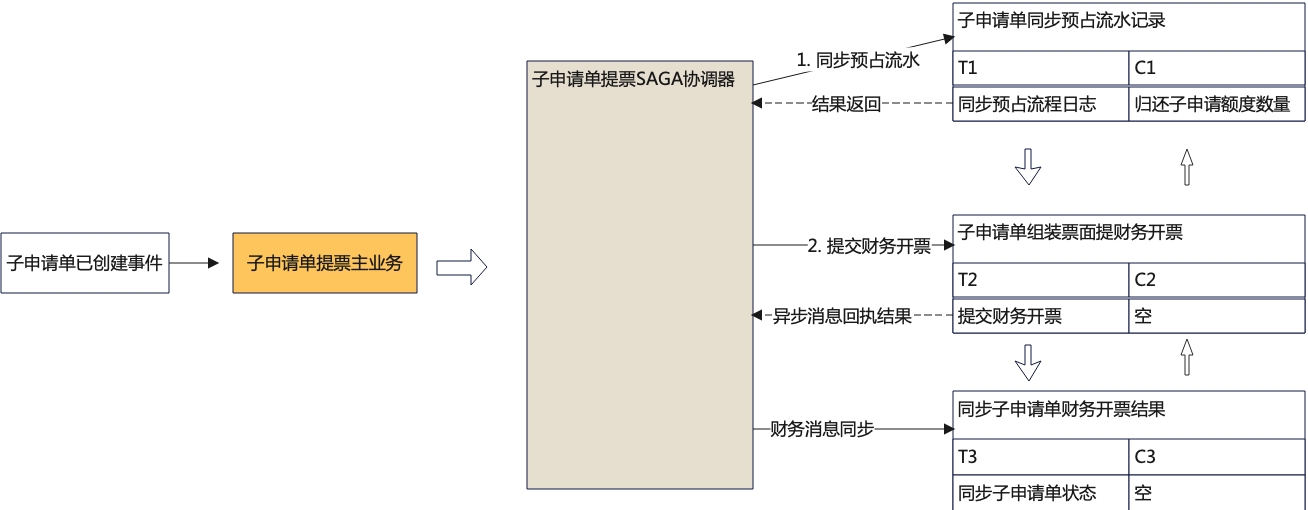
双精度浮点数用1位表示符号位，11位表示指数位，52位表示小数位，如下图所示：

在这里插入图片描述
符号位：正数为0，负数为1；
指数位：阶数+偏移量，阶数是：2^e-1^-1

e为阶码的位数。偏移量是把小数点移动到整数位只有1时移动的位数，正数表示向左移，负数表示向右移；

小数位：即二进制小数点后面的数。

接下来把0.1转成的二进制0.0001100110011001 …转成浮点数形式的二进制。

先要把小数点移动到整数位只有1，要向右移动4位，故偏移量为−4，通过指位数的计算公式2^11-1^-1-4=1019。

把1019转成二进制为1111111011，不够11位要补零，最终得出指位数为01111111011；

小数位为100110011001… ，因为小数位只能保留52位，第53位为1故进1。

转换结果如下图所示：

在这里插入图片描述
同理，再把 0.2 转成的二进制0.0011 0011 0011 0011… 转成浮点数形式的二进制，转换结果如下图所示：

在这里插入图片描述

2、浮点数相加

浮点数相加时，需要先比较指位数是否一致，如果一致则小数位直接相加，如果不一致，要先把指位数调成一致的，指位数小的向大的调整。

为了行文方便，把0.1转成的浮点数称为为0.1，把0.2转成的浮点数称为0.2。

0.1的指数位是1019 ，0.2的指数位是1020 。故要把0.1的指数位加1，即把0.1的小数点向左移动1位，另外浮点数的整数位固定为1，过程如下所示

浮点数相加时，需要先比较指位数是否一致，如果一致则小数位直接相加，如果不一致，要先把指位数调成一致的，指位数小的向大的调整。

为了行文方便，把0.1转成的浮点数称为为0.1，把0.2转成的浮点数称为0.2。

0.1的指数位是1019 ，0.2的指数位是1020 。故要把0.1的指数位加1，即把0.1的小数点向左移动1位，另外浮点数的整数位固定为1，过程如下所示

1.1001100110011001100110011001100110011001100110011010   原先
0.11001100110011001100110011001100110011001100110011010  移动后  
0.1100110011001100110011001100110011001100110011001101   将小数的第53位舍去，因为为0故不需进1

导致0.1的小数位变成如下所示：

在这里插入图片描述
会发现现在的小数位多出了一位，超出了52位，故要把小数位最后一位截掉，小数位最后一位是1，故要进1，如下所示：

10110011001100110011001100110011001100110011001100111
1011001100110011001100110011001100110011001100110100

截掉小数位的最后一位相当把小数点向左移了一位，故指数位要加1，此时的指数是0.2的指数1021 ，加1后变成1021 ，转成二进制为01111111101 ，那么相加后的浮点数如下所示：

在这里插入图片描述

3、浮点数转成十进制

在这里插入图片描述

因此，0.1+0.2 不等于 0.3 ，因为在 0.1+0.2 的计算过程中发生了两次精度丢失。

第一次是在 0.1 和 0.2 转成双精度二进制浮点数时，由于二进制浮点数的小数位只能存储52位，导致小数点后第53位的数要进行为1则进1为0则舍去的操作，从而造成一次精度丢失。
第二次在 0.1 和 0.2 转成二进制浮点数后，二进制浮点数相加的过程中，小数位相加导致小数位多出了一位，又要让第53位的数进行为1则进1为0则舍去的操作，又造成一次精度丢失。最终导致 0.1+0.2 不等于0.3 。

所以，在进行浮点数计算的时候，通常采用BigDecimal。