排序算法的空间复杂度和时间复杂度

news2024/11/23 1:55:18

一、排序算法的时间复杂度和空间复杂度

排序算法

平均时间复杂度

最坏时间复杂度

最好时间复杂度

空间复杂度

稳定性

冒泡排序

O(n²)

O(n²)

O(n)

O(1)

稳定

直接选择排序

O(n²)

O(n²)

O(n²)

O(1)

不稳定

直接插入排序

O(n²)

O(n²)

O(n)

O(1)

稳定

快速排序

O(nlogn)

O(n²)

O(nlogn)

O(nlogn)

不稳定

堆排序

O(nlogn)

O(nlogn)

O(nlogn)

O(1)

不稳定

归并排序

O(nlogn)

O(nlogn)

O(nlogn)

O(n)

稳定

希尔排序

O(nlogn)

O(n²)O(nlogn)

O(1)

不稳定

计数排序

O(n+k)

O(n+k)

O(n+k)

O(n+k)

稳定

基数排序

O(N*M) 

O(N*M)

O(N*M)

O(M)

稳定

注：

1 归并排序可以通过手摇算法将空间复杂度降到O(1)，但是时间复杂度会提高。

2 基数排序时间复杂度为O(N*M)，其中N为数据个数，M为数据位数。

1.1 复杂度辅助记忆

  1. 冒泡、选择、直接 排序需要两个for循环，每次只关注一个元素，平均时间复杂度为O(n²)）（一遍找元素O(n)，一遍找位置O(n)）
  2. 快速、归并、希尔、堆基于二分思想，log以2为底，平均时间复杂度为O(nlogn)（一遍找元素O(n)，一遍找位置O(logn)）

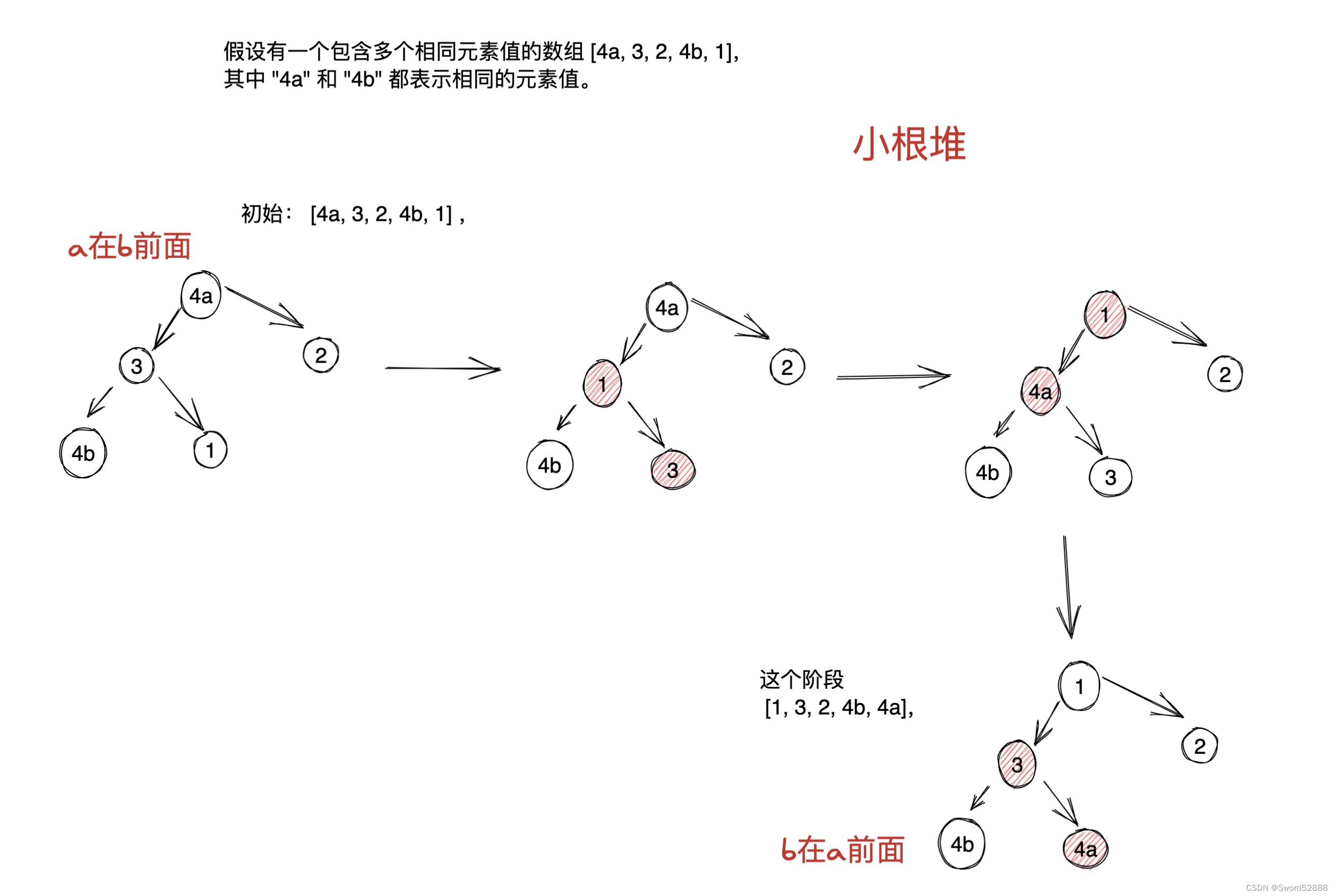
1.2 稳定性辅助记忆

  • 稳定性记忆-“快希选堆”（快牺牲稳定性） 
  • 排序算法的稳定性：排序前后相同元素的相对位置不变，则称排序算法是稳定的；否则排序算法是不稳定的。

二、理解时间复杂度

2.1 常数阶O(1)

int i = 1;
int j = 2;
++i;
j++;
int m = i + j;

 2.2 对数阶O(logN)

int i = 1;
while(i<n)
{
    i = i * 2;
}

2.3 线性阶O(n)

for(i=0; i<=n; i++)
{
   System.out.println("hello");
}

2.4 线性对数阶O(n)

for(m=1; m<n; m++)
{
    i = 1;
    while(i<n)
    {
        i = i * 2;
    }
}

2.5 平方阶O(n)


for(x=1; i<=n; x++)
{
   for(i=1; i<=n; i++)
    {
       System.out.println("hello");
    }
}

2.6 K次方阶O(n)

    for(i=0; i<=n; i++)
        {
            for(j=0; i<=n; i++)
            {
                for(k=0; i<=n; i++)
                {
                    System.out.println("hello");
                }
            }
        }


// k = 3 , n ^ 3

上面从上至下依次的时间复杂度越来越大，执行的效率越来越低。

三、空间复杂度

3.1 常数阶O(1) —— 原地排序

只用到 temp 这么一个辅助空间

原地排序算法，就是空间复杂度为O(1)的算法，不牵涉额外得到其他空间~

    private static void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

2.2 对数阶O(logN)

2.3 线性阶O(n)

        int[] newArray = new int[nums.length];
        for (int i = 0; i < nums.length; i++) {
            newArray[i] = nums[i];
        }

四、排序算法

4.1 冒泡排序

（思路：大的往后放）

4.1.1 代码

    private static void bubbleSort(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            for (int j = 0; j < nums.length - 1 - i; j++) {
                if (nums[j] > nums[j + 1]) {
                    swap(nums, j, j + 1);
                }
            }
        }
    }

4.1.2 复杂度

时间复杂度： N^2

空间复杂度：1

最佳时间复杂度：N^2  (因为就算你内部循环只对比，不交换元素，也是一样是N）

稳定性：稳定的 （大于的才换，小于等于的不交换）

    // { 0,1,2,3,4}
    private static void bubbleSort(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            boolean isChange = false;
            for (int j = 0; j < nums.length - 1 - i; j++) {
                if (nums[j] > nums[j + 1]) {
                    swap(nums, j, j + 1);
                    isChange = true;
                }
            }
            if(!isChange){
                return;
            }
        }
    }

改进后的代码，最佳时间复杂度： N  （因为假如第一轮对比就没有任何元素交换，那么可以直接退出，也就是只有一次外循环）

4.2 选择排序

（思路：最小的放最前）

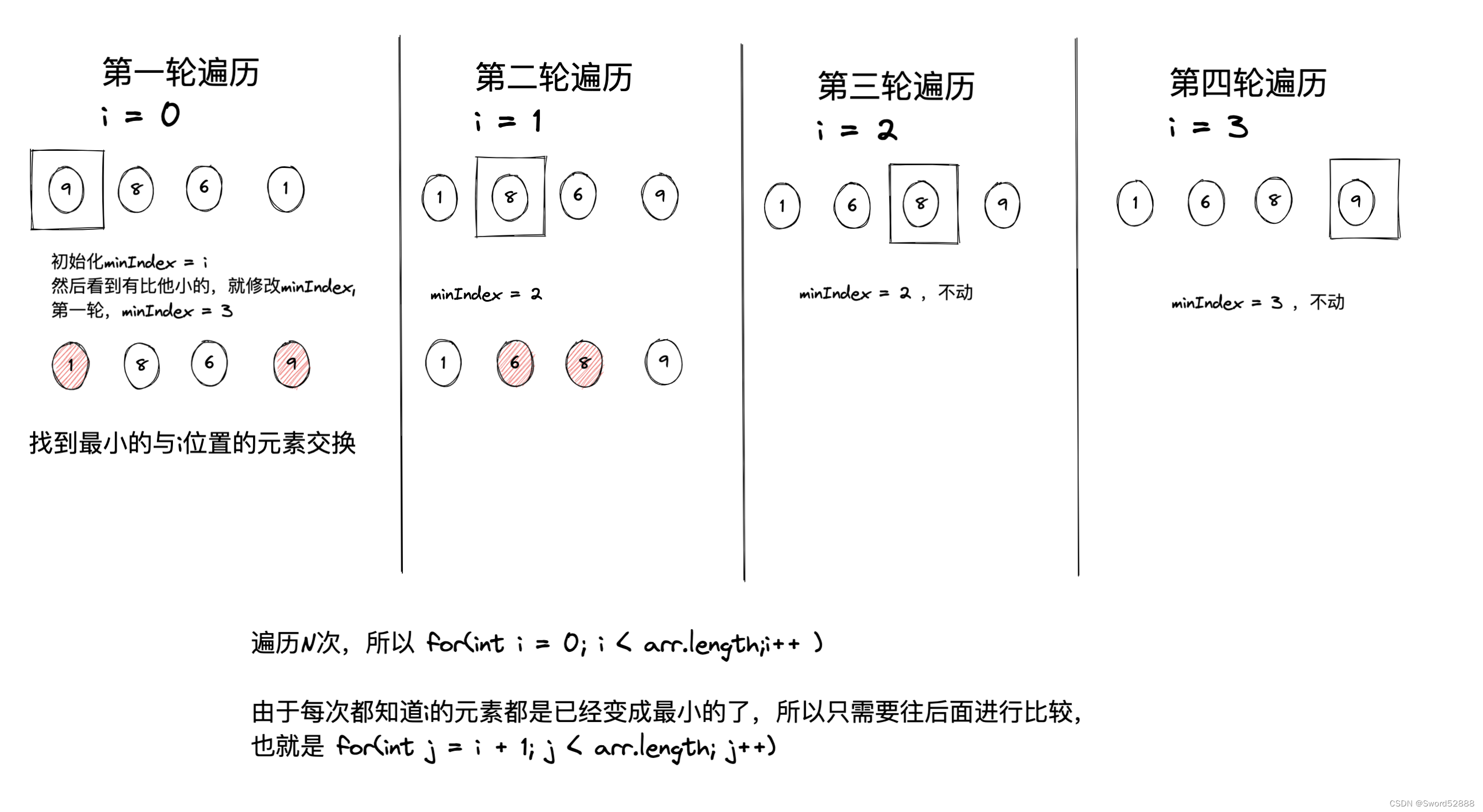
4.2.1 代码

private static void selectSort(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            int minIndex = i;
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[j] < nums[minIndex]) {
                    minIndex = j;
                }
            }
            swap(nums,minIndex,i);
        }
    }

4.2.2 复杂度

时间复杂度： N^2

空间复杂度：1

最佳时间复杂度：N^2  

稳定性：不稳定的 

4.3 直接插入排序

（思路：往排序好的数组中，找到合适的位置插进去）

4.3.1 代码

private static void insertSort(int[] nums) {
        for (int i = 1; i < nums.length; i++) {
            int temp = nums[i];
            int j = i - 1;
            for (; j >= 0 && temp < nums[j]; j--) {
                nums[j + 1] = nums[j];
            }
            nums[j + 1] = temp;
        }
    }

4.3.2 复杂度

时间复杂度： N^2

空间复杂度：1

最佳时间复杂度：N  (因为你不进入内部循环。 [1,2,3,4,5]）

稳定性：稳定的 

4.4 快速排序

（思路：利用数字target，把数组切成两边，左边比 target大，后边比 target小）

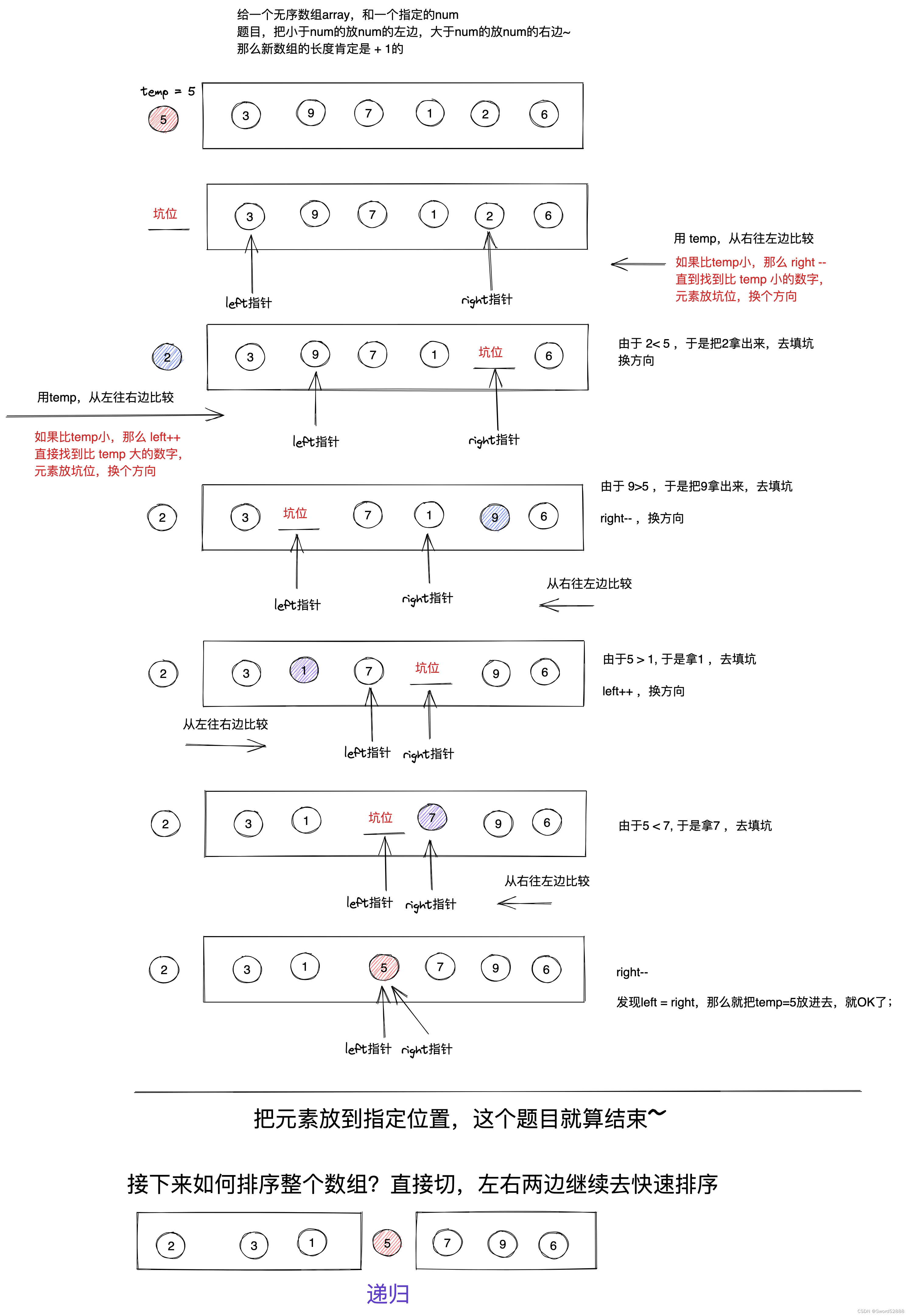
4.4.1 代码

/**
 * 快速排序算法
 * @param nums 待排序的数组
 * @param beginIndex 排序起始索引
 * @param endIndex 排序结束索引
 */
private static void quickSort(int[] nums, int beginIndex, int endIndex) {
    if (beginIndex >= endIndex) {
        return; // 递归终止条件：当开始索引大于等于结束索引时，表示已经完成排序
    }
    int mid = getMid(nums, beginIndex, endIndex); // 获取中间索引，用于分割数组
    quickSort(nums, beginIndex, mid - 1); // 对中间索引左侧的数组进行快速排序
    quickSort(nums, mid + 1, endIndex); // 对中间索引右侧的数组进行快速排序
}

/**
 * 获取分区中的中间元素的索引
 * @param nums 待排序的数组
 * @param beginIndex 分区的起始索引
 * @param endIndex 分区的结束索引
 * @return 中间元素的索引
 */
private static int getMid(int[] nums, int beginIndex, int endIndex) {
    int target = nums[beginIndex]; // 以数组的起始元素作为基准值
    int left = beginIndex;
    int right = endIndex;
    boolean right2left = true; // 标识位，表示当前从右往左搜索
    while (right > left) {
        if (right2left) {
            while (right > left && nums[right] > target) {
                right--;
            }
            if (right > left) {
                nums[left] = nums[right]; // 当右侧元素较大时，将右侧元素移到插入位置
                right2left = false; // 切换为从左往右搜索
            }
        } else {
            while (right > left && nums[left] < target) {
                left++;
            }
            if (right > left) {
                nums[right] = nums[left]; // 当左侧元素较小时，将左侧元素移到插入位置
                right2left = true; // 切换为从右往左搜索
            }
        }
    }
    nums[left] = target; // 将基准值放入插入位置，完成一轮交换
    return left;
}

4.4.2 复杂度

时间复杂度： N Log N （每个元素找到中间位置的，需要 LogN 时间，N个元素就是NLogN）

空间复杂度：N Log N （递归调用，需要栈空间）

最差时间复杂度：N ^ 2  （ 比如正序数组 [1,2,3,4,5] ）

稳定性：不稳定的 

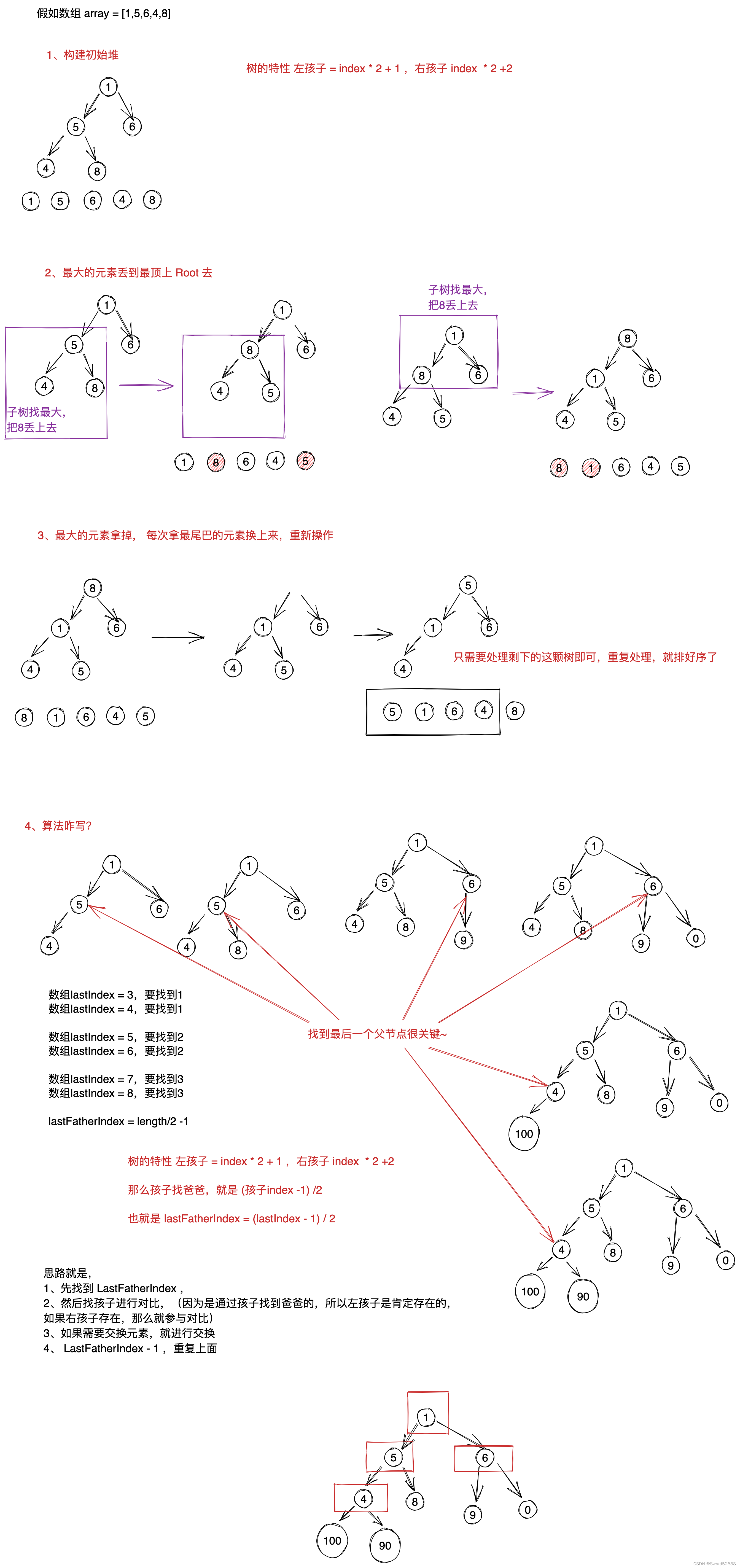
4.5 堆排序

（思路：最大放上面，然后与最后元素交换，继续建堆）

4.5.1 代码

/**
 * 堆排序算法
 * @param nums 待排序的数组
 * @param beginIndex 排序的起始索引
 * @param endIndex 排序的结束索引
 */
private static void heapSort(int[] nums, int beginIndex, int endIndex) {
    if (beginIndex >= endIndex) {
        return; // 当开始索引大于等于结束索引时，排序完成
    }
    for (int i = endIndex; i >= beginIndex; i--) {
        createHeap(nums, i); // 构建最大堆
        swap(nums, 0, i); // 将最大元素移到数组末尾
    }
}

/**
 * 构建最大堆
 * @param nums 待构建的数组
 * @param endIndex 当前堆的结束索引
 */
private static void createHeap(int[] nums, int endIndex) {
    int lastFatherIndex = (endIndex - 1) / 2;
    for (int i = lastFatherIndex; i >= 0; i--) {
        int biggestIndex = i;
        int leftChildIndex = i * 2 + 1;
        int rightChildIndex = i * 2 + 2;
        if (leftChildIndex <= endIndex) {
            biggestIndex = nums[biggestIndex] > nums[leftChildIndex] ? biggestIndex : leftChildIndex;
        }
        if (rightChildIndex <= endIndex) {
            biggestIndex = nums[biggestIndex] > nums[rightChildIndex] ? biggestIndex : rightChildIndex;
        }
        swap(nums, biggestIndex, i); // 调整堆，确保最大元素位于堆顶
    }
}

/**
 * 交换数组中两个元素的位置
 * @param nums 数组
 * @param i 索引1
 * @param j 索引2
 */
private static void swap(int[] nums, int i, int j) {
    int temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
}

4.5.2 复杂度

时间复杂度： N Log N （每个元素都要构建1次堆，需要 LogN 时间，N个元素就是NLogN，任何情况下都一样）

空间复杂度：1 （原地排序）

最差时间复杂度：N ^ 2  （ 比如正序数组 [1,2,3,4,5] ）

稳定性：不稳定的 

4.6 归并排序

递归思路，左右两边排序好了，就已经排序好了

4.6.1 代码

// 归并排序的主方法
private static void mergeSort(int[] nums, int beginIndex, int endIndex) {
    // 如果起始索引大于等于结束索引，表示只有一个元素或没有元素，不需要排序
    if (beginIndex >= endIndex) {
        return;
    }
    
    // 计算数组的中间索引
    int mid = beginIndex + (endIndex - beginIndex) / 2;
    
    // 递归排序左半部分
    mergeSort(nums, beginIndex, mid);
    
    // 递归排序右半部分
    mergeSort(nums, mid + 1, endIndex);
    
    // 合并左右两部分
    merge(nums, beginIndex, mid, endIndex);
}

// 合并函数，用于将左右两部分合并成一个有序的数组
private static void merge(int[] nums, int beginIndex, int mid, int endIndex) {
    int left = beginIndex;
    int right = mid + 1;
    int[] newArrays = new int[endIndex - beginIndex + 1];
    int newArraysIndex = 0;

    // 比较左右两部分的元素，将较小的元素放入新数组
    while (left <= mid && right <= endIndex) {
        newArrays[newArraysIndex++] = nums[left] <= nums[right] ? nums[left++] : nums[right++];
    }

    // 将剩余的左半部分元素复制到新数组
    while (left <= mid) {
        newArrays[newArraysIndex++] = nums[left++];
    }

    // 将剩余的右半部分元素复制到新数组
    while (right <= endIndex) {
        newArrays[newArraysIndex++] = nums[right++];
    }

    // 将合并后的新数组复制回原数组
    for (int i = 0; i < newArrays.length; i++) {
        nums[beginIndex + i] = newArrays[i];
    }
}

4.6.2 复杂度

时间复杂度： N Log N （每个元素都要递归，需要 LogN 时间，N个元素就是NLogN，任何情况下都一样）

空间复杂度：N

稳定性：稳定的 

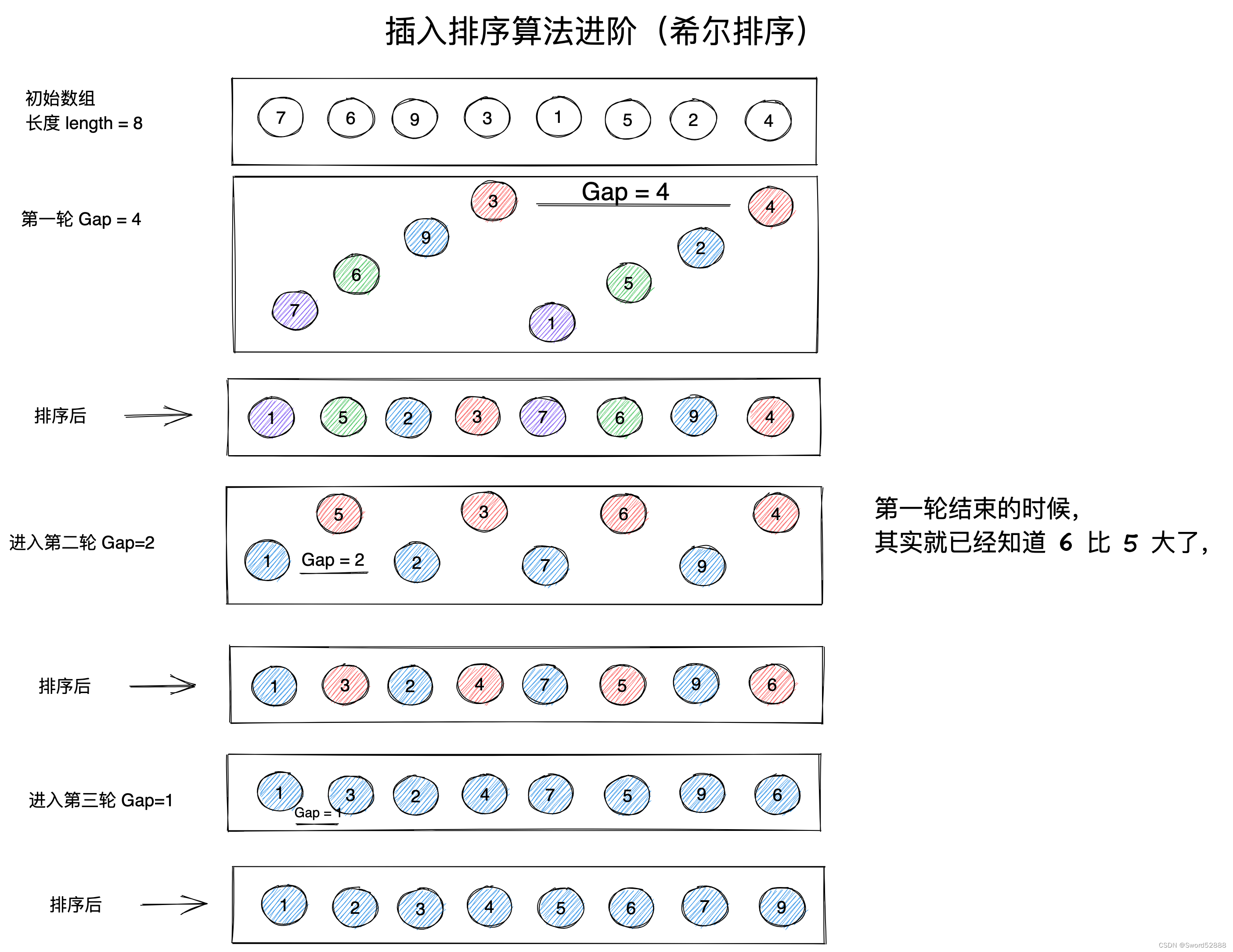
 4.7 希尔排序

思路：直接插入排序的升级版（分段式插入排序）

4.7.1 代码

private static void quickSort(int[] nums) {
//        int gap = nums.length / 2;
//        while (gap > 0) {
        for (int i = 1; i < nums.length; i++) {
            int temp = nums[i];
            int j;
            for (j = i - 1; j >= 0 && temp < nums[j]; j--) {
                nums[j + 1] = nums[j];
            }
            nums[j + 1] = temp;
        }
//        gap = gap / 2;
//        }
    }

    // 把上面的快速排序改成shell排序，只需要把间隔1 改成gap
    private static void shellSort(int[] nums) {
        int gap = nums.length / 2;
        while (gap > 0) {
            for (int i = gap; i < nums.length; i++) {
                int temp = nums[i];
                int j;
                for (j = i - gap; j >= 0 && temp < nums[j]; j = j - gap) {
                    nums[j + gap] = nums[j];// 如果当前元素比待插入元素大，将当前元素向后移动
                }
                nums[j + gap] = temp; // 因为上边 j=j-gap退出的时候，j已经被剪掉1次了，可能小于0了
            }
            gap = gap / 2;
        }
    }

4.7.2 复杂度

时间复杂度： N Log N 

空间复杂度：1

稳定性：稳定的 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1185273.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

node插件MongoDB（一）——MongoDB的下载和安装

node插件MongoDB（一）——MongoDB的下载和安装

文章目录 前言一、MongoDB的下载和安装1. 下载(1) 打开官网(2) 选择版本(3) 选择电脑系统和安装格式后点击下载(4) 将文件解压放到C:\Program Files文件目录下(5) 在c盘下创建文件夹(6) 启动服务端程序(7) 服务端程序启动成功效果(8) 在浏览器中输入127.0.0.1:27017查看效果&am…
阅读更多...
linux下IO模及其特点及select

linux下IO模及其特点及select

ftp实现 模拟FTP核心原理&#xff1a;客户端连接服务器后&#xff0c;向服务器发送一个文件。文件名可以通过参数指定&#xff0c;服务器端接收客户端传来的文件&#xff08;文件名随意&#xff09;&#xff0c;如果文件不存在自动创建文件&#xff0c;如果文件存在&#xff0c…
阅读更多...
nacos应用——占用内存过多问题解决（JVM调优初步）

nacos应用——占用内存过多问题解决（JVM调优初步）

问题描述 最近搞了一台1年的阿里云服务器&#xff0c;安装了一下常用的MySQL&#xff0c;Redis&#xff0c;rabbitmq&#xff0c;minio&#xff0c;然后有安装了一下nacos&#xff0c;结果一启动nacos内存占用就很高&#xff0c;就比较限制我继续安装其他镜像或者启动别的服务…
阅读更多...
龙迅LT8911EXB功能概述 MIPICSI/DSI TO EDP

龙迅LT8911EXB功能概述 MIPICSI/DSI TO EDP

LT8911EXB 描述&#xff1a; Lontium LT8911EXB是MIPIDSI/CSI到eDP转换器&#xff0c;单端口MIPI接收器有1个时钟通道和4个数据通道&#xff0c;每个数据通道最大运行2.0Gbps&#xff0c;最大输入带宽为8.0Gbps。转换器解码输入MIPI RGB16/18/24/30/36bpp、YUV422 16/20/24bp…
阅读更多...
84 柱状图中的最大的矩形（单调栈）

84 柱状图中的最大的矩形（单调栈）

题目 柱状图中的最大的矩形 给定 n 个非负整数&#xff0c;用来表示柱状图中各个柱子的高度。每个柱子彼此相邻&#xff0c;且宽度为 1 。 求在该柱状图中&#xff0c;能够勾勒出来的矩形的最大面积。 示例 1: 输入&#xff1a;heights [2,1,5,6,2,3] 输出&#xff1a;10 …
阅读更多...
webpack的简单使用

webpack的简单使用

什么是webpack&#xff08;去官网看详细的API&#xff09; 本质上&#xff0c;webpack 是一个用于现代 JavaScript 应用程序的 静态模块打包工具。当 webpack 处理应用程序时&#xff0c;它会在内部从一个或多个入口点构建一个 依赖图(dependency graph)&#xff0c;然后将你项…
阅读更多...
ATFX汇市：欧元区9月PPI年率降幅扩大至12.4%，EURUSD反弹不够流畅

ATFX汇市：欧元区9月PPI年率降幅扩大至12.4%，EURUSD反弹不够流畅

ATFX汇市&#xff1a;2023年9月欧元区生产者物价指数PPI同比下降12.4%&#xff0c;上月下降11.5%&#xff0c;而市场普遍预期下降12.5%&#xff0c;表现较差。12.4%的降幅创出PPI数据有记录以来的最低值&#xff0c;可见欧元区生产端的通缩形势严峻。跌幅最大的品种是能源&…
阅读更多...
进程（3）——进程优先级与环境变量【Linux】

进程（3）——进程优先级与环境变量【Linux】

进程&#xff08;3&#xff09;——进程优先级与环境变量【Linux】 一. 进程如何在cpu中如何执行1.1进程在CPU中的特性1.2 寄存器1.2.1 进程的上下文 二. 进程优先级2.1 如何查看进程优先级2.2 修改进程的优先级2.2.1 NI值2.2.2 修改方法 三. 环境变量3.1 什么是环境变量&#…
阅读更多...
二十、泛型（4）

二十、泛型（4）

本章概要 补偿擦除 创建类型的实例泛型数组 补偿擦除 因为擦除&#xff0c;我们将失去执行泛型代码中某些操作的能力。无法在运行时知道确切类型&#xff1a; //无法编译 public class Erased<T> {private final int SIZE 100;public void f(Object arg) {// error…
阅读更多...
手机玻璃盖板为什么需要透光率检测

手机玻璃盖板为什么需要透光率检测

手机盖板&#xff0c;也称为手机壳或保护套&#xff0c;是一种用于保护手机外观和延长使用寿命的装置。它们通常由塑料、硅胶、玻璃或金属等材料制成&#xff0c;并固定在手机外壳上,其中任何一个工序出现差错&#xff0c;都有可能导致手机盖板产生缺陷&#xff0c;例如漏油、透…
阅读更多...
维控PLC——LX1S ：编程口通讯协议

维控PLC——LX1S ：编程口通讯协议

文章目录 说明通讯帧通讯命令字通讯数据地址维控 LX1S通讯协议举例 说明 该协议适用于维控LX1S系列PLC&#xff0c;关于维控LX2N的协议将在后面描述。 通讯帧 通讯采用ASCII码&#xff0c;校验方式采用和校验。 请求帧格式:报文开始命令字地址&#xff08;有些无&#xff09…
阅读更多...
热门的免费报表软件，建议收藏！

热门的免费报表软件，建议收藏！

目前&#xff0c;随着企业对数据越来越重视&#xff0c;报表软件的应用越来越广泛。企业报表的需求越来越多变&#xff0c;就需要好用的免费报表软件&#xff0c;报表软件必须具备简捷、专业、灵活的特点&#xff0c;这里就给大家测评几款免费报表软件&#xff0c;供大家做参考…
阅读更多...
机器学习模板代码（期末考试复习）自用存档

机器学习模板代码（期末考试复习）自用存档

机器学习复习代码 利用sklearn实现knn import numpy as np import pandas as pd from sklearn.neighbors import KNeighborsClassifier from sklearn.model_selection import GridSearchCVdef model_selection(x_train, y_train):## 第一个是网格搜索## p是选择查找方式:1是欧…
阅读更多...
JVM之jps虚拟机进程状态工具

JVM之jps虚拟机进程状态工具

jps虚拟机进程状态工具 1、jps jps&#xff1a;(JVM Process Status Tool)&#xff0c;虚拟机进程状态工具&#xff0c;可以列出正在运行的虚拟机进程&#xff0c;并显示虚拟机执 行主类&#xff08;Main Class&#xff0c;main()函数所在的类&#xff09;的名称&#xff0c…
阅读更多...
公司来了个00后，起薪就是18K，不愧是卷王。。。

公司来了个00后，起薪就是18K，不愧是卷王。。。

前言 都在传00后躺平、整顿职场&#xff0c;但该说不说&#xff0c;是真的卷&#xff0c;感觉我都要被卷废了... 前段时间&#xff0c;公司招了一个年轻人&#xff0c;其中有一个是00后&#xff0c;工作才一年多&#xff0c;直接跳槽到我们公司&#xff0c;薪资据说有18K&…
阅读更多...
Java自学第6课：电商项目（1）

Java自学第6课：电商项目（1）

从本课开始&#xff0c;我们跟着项目一起来敲代码。通过项目来学习Java和Java web 1 开始 首先了解要做什么项目&#xff0c;这里选择B2C电商。 需求分析很重要&#xff0c;所以要了解甲方业务流程。 之后配置开发环境&#xff0c;选择开发工具。 然后就是搭建开发环境&…
阅读更多...
【16】c++11新特性 —＞弱引用智能指针weak_ptr（1）

【16】c++11新特性 —＞弱引用智能指针weak_ptr（1）

定义 std::weak_ptr&#xff1a;弱引用的智能指针&#xff0c;它不共享指针&#xff0c;不能操作资源&#xff0c;是用来监视 shared_ptr 中管理的资源是否存在。 use_count #include <iostream> #include <memory> using namespace std;int main() {shared_ptr…
阅读更多...
最终前端后端小程序还有nginx配置

最终前端后端小程序还有nginx配置

前端 前端 build 代码及其 放置位置 后端 nginx.conf 配置 user root;worker_processes auto; error_log /var/log/nginx/error.log notice; pid /var/run/nginx.pid;events {worker_connections 1024; }http {include /etc/nginx/mime.types;default_type a…
阅读更多...
SysML理论知识

SysML理论知识

概述 由来 长期以来系统工程师使用的建模语言、工具和技术种类很多&#xff0c;如行为图、IDEF0、N2图等&#xff0c;这些建模方法使用的符号和语义不同&#xff0c;彼此之间不能互操作和重用。系统工程正是由于缺乏一种强壮的标准的建模语言&#xff0c;从而限制系统工程师和…
阅读更多...
电商API接口多平台全面分类|接入方式|提供测试

电商API接口多平台全面分类|接入方式|提供测试

l 角色分类 对应角色主要包括&#xff1a; 依次表示公开查询应用、买家应用、卖家应用、商家应用、高级应用、专业应用被授权访问API的角色级别。其中公开查询应用为最低权限集合级别、专业 应用为最高权限集合级别。查、买、卖接口无需审批&#xff0c;仅受默认流量规则限制…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023