思路

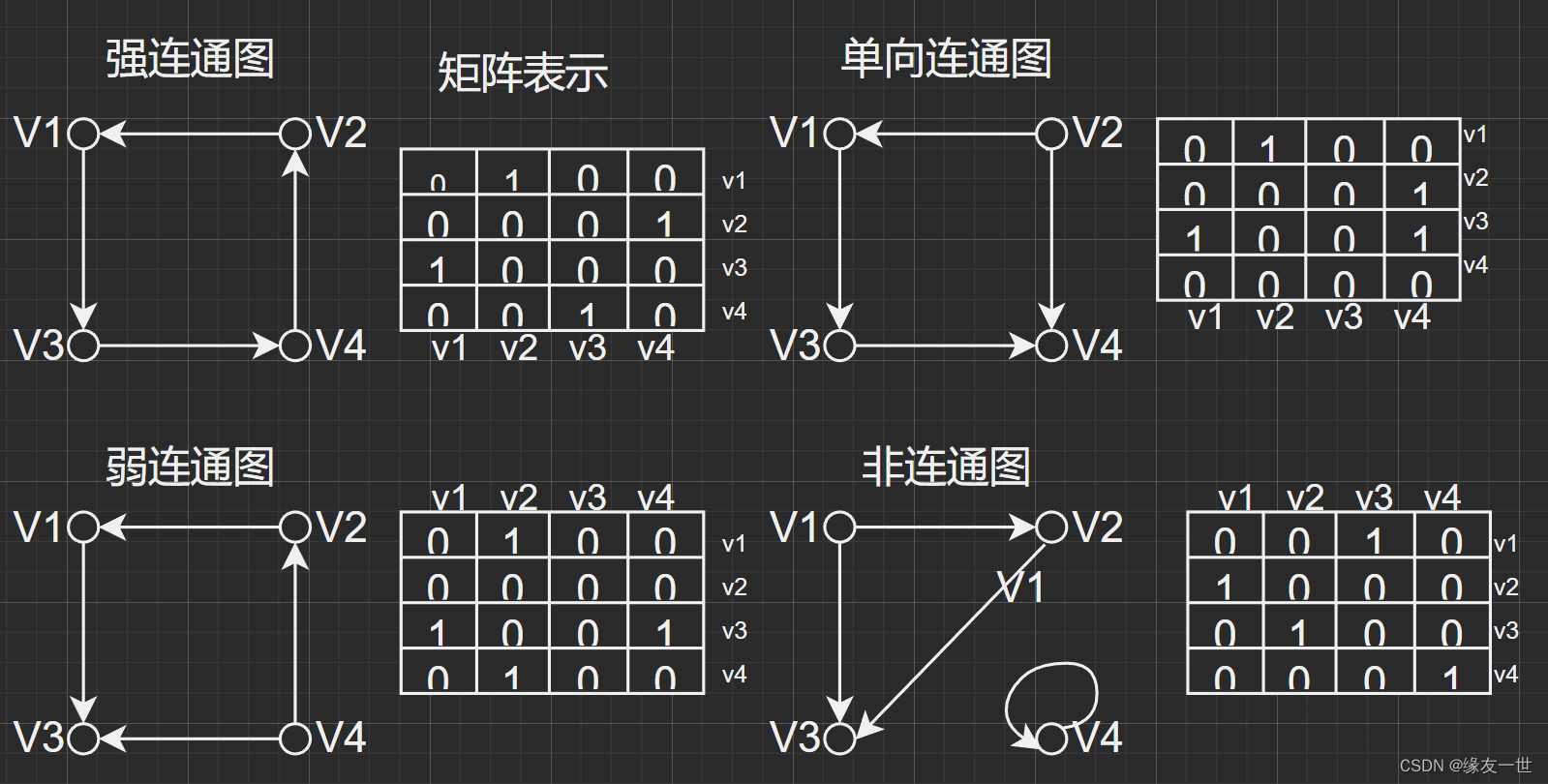
• 对于给定的邻接矩阵 A，可以用可达矩阵 Warshall 算法求出 A 所表示的图的可达矩阵 P。
  • 对于可达矩阵 P 来说，如果 P 的所有元素均为 $1$，则所给的有向图是强连通的；
  • 对于 P 的所有元素（除主对角线元素外）$P_{ij}$ 来说，均有：$P_{ij}+P_{ij}>0$，则所给有向图是单向连通的。
  • 当所给有向图既不是强连通的，又不是单向连通的时候，我们改造邻接矩阵为：对于矩阵 A 中所有的元素（除主对角线的元素外）$a_{ij}$，若$a_{ij}=1$ 或$a_{ji}=1$，则 $a_{ij}=a_{ji}=1$。
  • 对于这样改造之后所得到的新的矩阵 $A^{\prime }$（$A^{\prime }$相当于原有向图忽略方向之后所得到的无向图的邻接矩阵），再用方法进行判断，当 $P^{\prime }$的所有元素（除主对角线的元素外）均为 $1$时，原有向图是弱连通图；
  • 否则，原有向图是不连通的。

重要算法&Warshall 算法

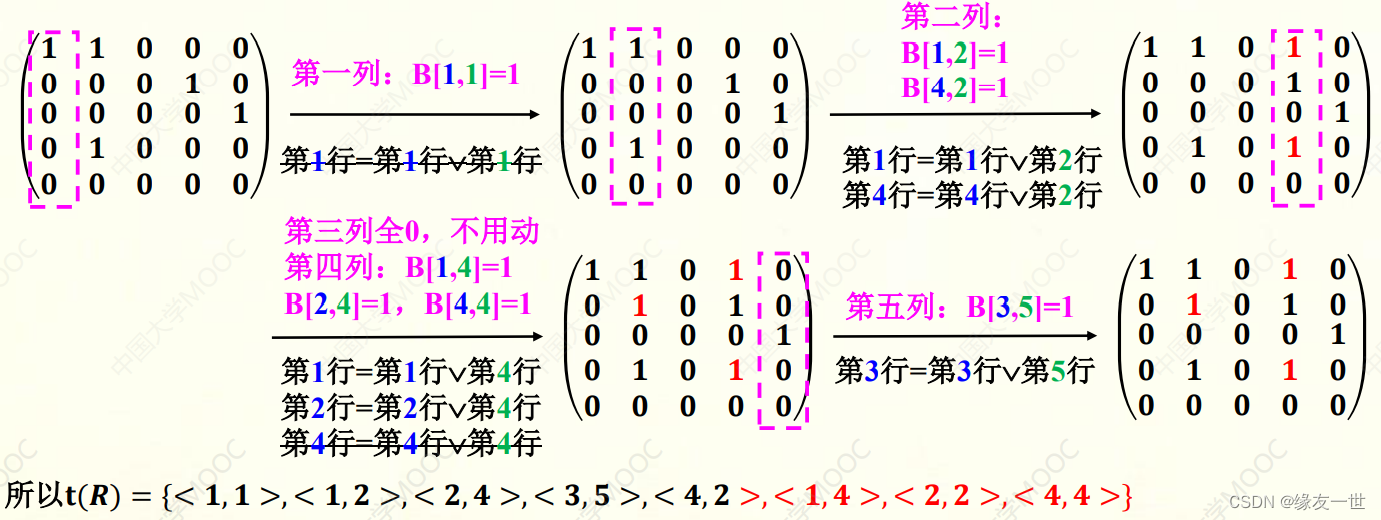
• 认真看图，认真体会

代码

public static void warshall(int[][] matrix) {
    int cols=0,rows=0,i=0;
    for(cols=0;cols<matrix.length;cols++) {
        for(rows=0;rows<matrix.length;rows++) {
            if(matrix[rows][cols]==1) {
                for(i=0;i<matrix.length;i++) {
                    matrix[rows][i]=matrix[rows][i] | matrix[cols][i];
                }
            }
        }
    }
}

全部代码

package 离散数学;

import java.util.Scanner;

/**
 * @author 缘友一世
 * date 2022/12/27-14:50
 */
public class demo03 {
    public static void main(String[] args) {
        int nums=0;
        Scanner scanner = new Scanner(System.in);
        System.out.print("请输入结点的个数：");
        if(scanner.hasNextInt()) {
            nums=scanner.nextInt();
        }
        int[][] matrix=new int[nums][nums];
        System.out.println("请输入"+nums+"阶矩阵的值[以空格隔开]:");
        for(int i=0;i<matrix.length;i++) {
            for(int j=0;j<matrix[i].length;j++) {
                if(scanner.hasNextInt()) {
                    matrix[i][j]= scanner.nextInt();
                }
            }
        }
        warshall(matrix);
        display(matrix);
        int res = estimate(matrix);
        if(res==1) {
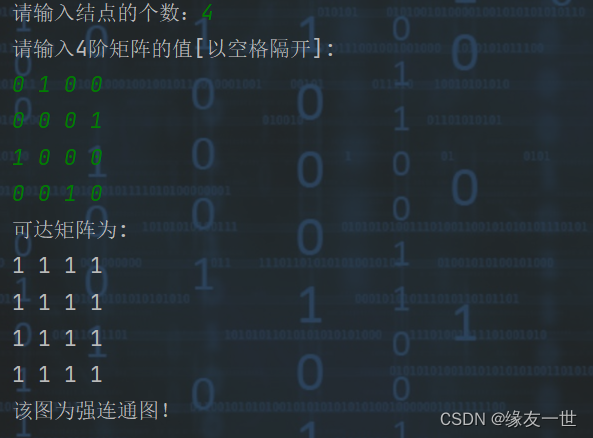
            System.out.println("该图为强连通图！");
        }else if(res==0) {
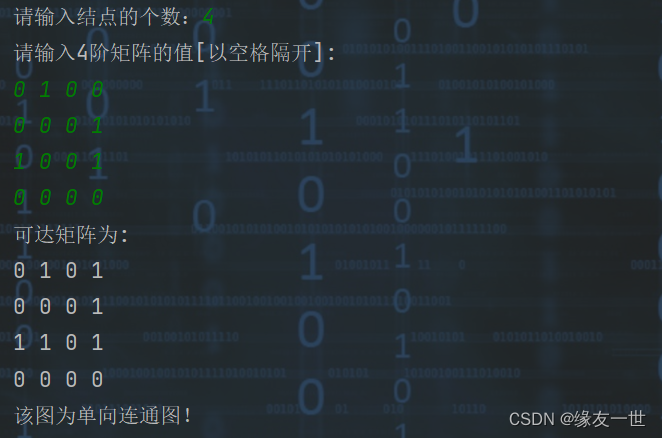
            System.out.println("该图为单向连通图！");
        }else if(res==-1){
            transform(matrix);
            System.out.print("改造后");
            display(matrix);
            res=estimate02(matrix);
            if(res==1) {
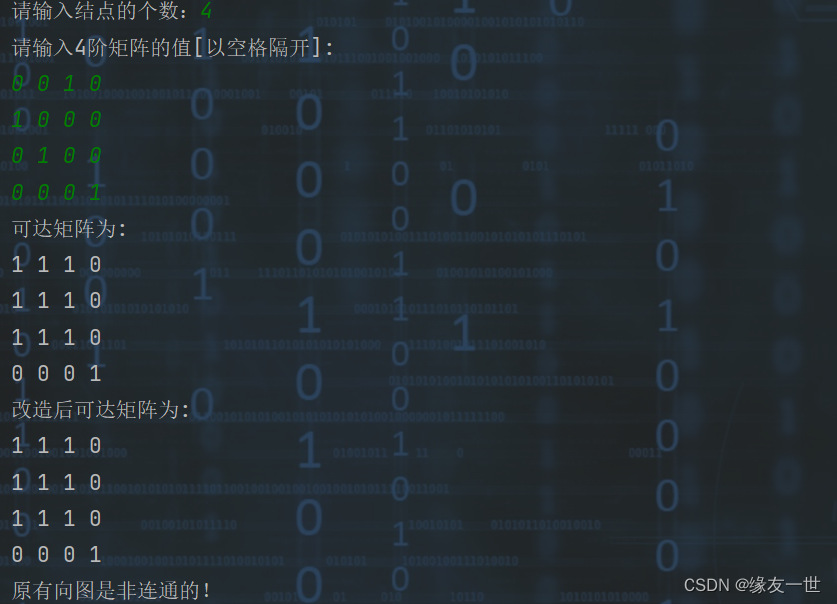
                System.out.println("原有向图是弱连通的！");
            }else {
                System.out.println("原有向图是非连通的！");
            }
        }
    }
    public static void warshall(int[][] matrix) {
        int cols=0,rows=0,i=0;
        for(cols=0;cols<matrix.length;cols++) {
            for(rows=0;rows<matrix.length;rows++) {
                if(matrix[rows][cols]==1) {
                    for(i=0;i<matrix.length;i++) {
                        matrix[rows][i]=matrix[rows][i] | matrix[cols][i];
                    }
                }
            }
        }
    }
    public static void display(int[][] matrix) {
        System.out.println("可达矩阵为:");
        for(int i=0;i<matrix.length;i++) {
            for(int j=0;j<matrix.length;j++) {
                System.out.print(matrix[i][j]+" ");
            }
            System.out.println();
        }
    }
    public static int estimate(int[][] matrix) {
        int flag=1;
        for(int i=0;i<matrix.length;i++) {
            for(int j=0;j<matrix.length;j++) {
                if(matrix[i][j]!=1) {
                    flag=-1;
                }
            }
        }
        //标志未改变，所以为强连通图
        if(flag==1) {
            return flag;
        }
        flag=0;//标记为单向连通
        for(int i=0;i<matrix.length;i++) {
            for(int j=0;j<matrix.length;j++) {
                if(i!=j && !(matrix[i][j]+matrix[j][i]>0)) {
                    flag=-1;
                }
            }
        }
        //单向连通图
        if(flag==0) {
            return flag;
        }
        //否则为弱连通
        return flag;
    }
    public static int estimate02(int[][] matrix) {
        int flag=1;
        for(int i=0;i<matrix.length;i++) {
            for(int j=0;j<matrix.length;j++) {
                if(i!=j && matrix[i][j]!=1) {
                    flag=-1;
                    return flag;
                }
            }
        }
        return flag;
    }
    public static void transform(int[][] matrix) {
        for(int i=0;i<matrix.length;i++) {
            for(int j=0;j<matrix.length;j++) {
                if(i!=j && (matrix[i][j]==1 || matrix[j][i]==1)){
                    matrix[i][j]=matrix[j][i]=1;
                }
            }
        }
    }
}

效果展示