文章目录
- 前言
- 一、数据集介绍
- 二、使用步骤
- 1.导包
- 1.2加载数据集
- 1.3绘制二维数据分布图
- 1.4实例化K-means类,并且定义训练函数
- 1.5训练
- 1.6可视化展示
- 2.聚类算法
- 2.1.可视化生成
- 3其他聚类算法进行鸢尾花分类
前言
例如:随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文就介绍了机器学习的基础内容。
一、数据集介绍
鸢尾花数据集:鸢尾花开源数据集,共包含150条记录
二、使用步骤
1.导包
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn import datasets
1.2加载数据集
# 直接从sklearn中获取数据集
iris = datasets.load_iris()
X = iris.data[:, :4] # 表示我们取特征空间中的4个维度
print(X.shape)
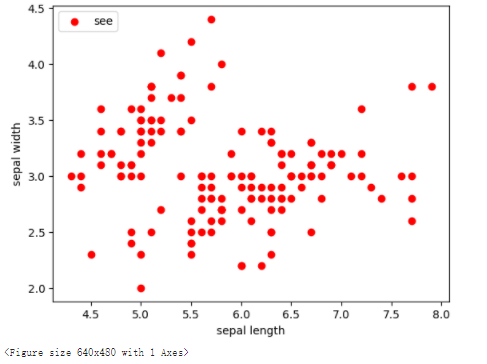
1.3绘制二维数据分布图
# 取前两个维度(萼片长度、萼片宽度),绘制数据分布图
plt.scatter(X[:, 0], X[:, 1], c="red", marker='o', label='see')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
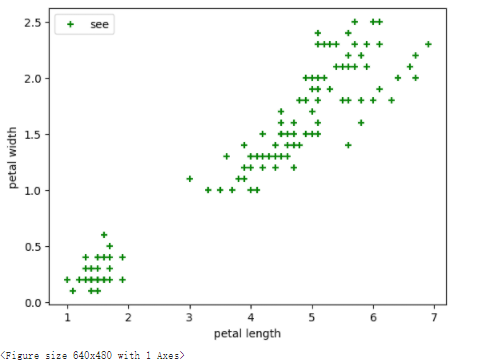
# 取后两个维度(花瓣长度、花瓣宽度),绘制数据分布图
plt.scatter(X[:, 2], X[:, 3], c="green", marker='+', label='see')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()
1.4实例化K-means类,并且定义训练函数
def Model(n_clusters):
estimator = KMeans(n_clusters=n_clusters)# 构造聚类器
return estimator
def train(estimator):
estimator.fit(X) # 聚类
1.5训练
# 初始化实例,并开启训练拟合
estimator=Model(4)
train(estimator)
1.6可视化展示
label_pred = estimator.labels_ # 获取聚类标签
# 绘制k-means结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
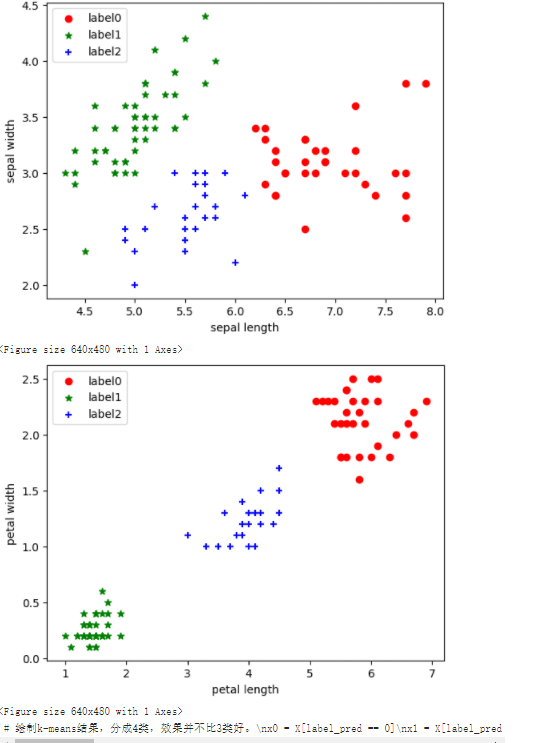
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
# 绘制k-means结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
plt.scatter(x0[:, 2], x0[:, 3], c="red", marker='o', label='label0')
plt.scatter(x1[:, 2], x1[:, 3], c="green", marker='*', label='label1')
plt.scatter(x2[:, 2], x2[:, 3], c="blue", marker='+', label='label2')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()
'''# 绘制k-means结果,分成4类,效果并不比3类好。
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
x3 = X[label_pred == 3]
plt.scatter(x0[:, 2], x0[:, 3], c="red", marker='o', label='label0')
plt.scatter(x1[:, 2], x1[:, 3], c="green", marker='*', label='label1')
plt.scatter(x2[:, 2], x2[:, 3], c="blue", marker='+', label='label2')
plt.scatter(x2[:, 2], x2[:, 3], c="yellow", marker='X', label='label3')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show() '''
2.聚类算法
代码如下(示例):
#1. 函数distEclud()的作用:用于计算两个向量的距离
def distEclud(x,y):
return np.sqrt(np.sum((x-y)**2))
#2. 函数randCent()的作用: 用来为给定的数据集构建一个包含k个随机质心的集合
def randCent(dataSet,k):
# 3.m,n分别被赋值为?
# m = 150 ,n = 4
m,n = dataSet.shape
centroids = np.zeros((k,n))
#4.补充range()中的参数
for i in range(k):
index = int(np.random.uniform(0,m)) # 产生0到150的随机数(在数据集中随机挑一个向量做为质心的初值)
centroids[i,:] = dataSet[index,:] #把对应行的四个维度传给质心的集合
# print(centroids)
return centroids
# k均值聚类算法
def KMeans(dataSet,k):
m = np.shape(dataSet)[0] #行数150
# 第一列存每个样本属于哪一簇(四个簇)
# 第二列存每个样本的到簇的中心点的误差
# print(m)
clusterAssment = np.mat(np.zeros((m,2)))# .mat()创建150*2的矩阵
clusterChange = True
# 5.centroids = randCent(dataSet,k)的作用:初始化质心centroids
centroids = randCent(dataSet,k)
# 6.补充while循环的条件。
while clusterChange:
clusterChange = False
# 遍历所有的样本
# 7.补充range()中的参数。
for i in range(m):
minDist = 100000.0
minIndex = -1
# 遍历所有的质心
#8.补充range()中的参数:
for j in range(k):
# 计算该样本到3个质心的欧式距离,找到距离最近的那个质心minIndex
distance = distEclud(centroids[j,:],dataSet[i,:])
if distance < minDist:
#9.补充minDist;minIndex的赋值代码
minDist = distance
#分类的索引
minIndex = j
# 更新该行样本所属的簇
if clusterAssment[i,0] != minIndex:
clusterChange = True
clusterAssment[i,:] = minIndex,minDist**2
#更新质心
for j in range(k):
pointsInCluster = dataSet[np.nonzero(clusterAssment[:,0].A == j)[0]] # 获取对应簇类所有的点(x*4)
#10.补充axis后的赋值:
centroids[j,:] = np.mean(pointsInCluster,axis=0) # 求均值,产生新的质心
# print(clusterAssment[0:150,:])
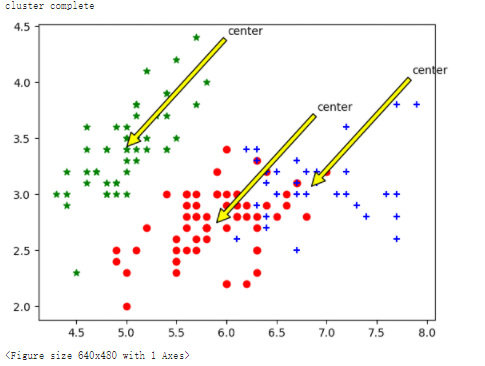
print("cluster complete")
return centroids,clusterAssment
def draw(data,center,assment):
length=len(center)
fig=plt.figure
data1=data[np.nonzero(assment[:,0].A == 0)[0]]
data2=data[np.nonzero(assment[:,0].A == 1)[0]]
data3=data[np.nonzero(assment[:,0].A == 2)[0]]
# 选取前两个维度绘制原始数据的散点图
plt.scatter(data1[:,0],data1[:,1],c="red",marker='o',label='label0')
plt.scatter(data2[:,0],data2[:,1],c="green", marker='*', label='label1')
plt.scatter(data3[:,0],data3[:,1],c="blue", marker='+', label='label2')
# 绘制簇的质心点
for i in range(length):
plt.annotate('center',xy=(center[i,0],center[i,1]),xytext=\
(center[i,0]+1,center[i,1]+1),arrowprops=dict(facecolor='yellow'))
# plt.annotate('center',xy=(center[i,0],center[i,1]),xytext=\
# (center[i,0]+1,center[i,1]+1),arrowprops=dict(facecolor='red'))
plt.show()
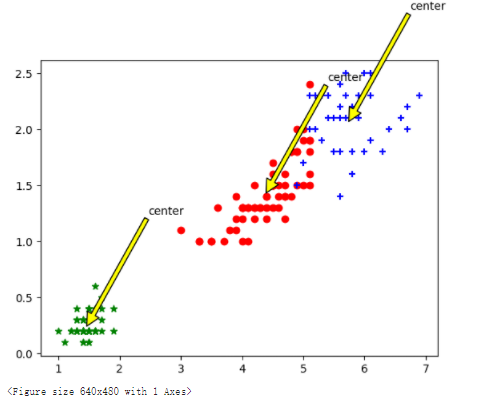
# 选取后两个维度绘制原始数据的散点图
plt.scatter(data1[:,2],data1[:,3],c="red",marker='o',label='label0')
plt.scatter(data2[:,2],data2[:,3],c="green", marker='*', label='label1')
plt.scatter(data3[:,2],data3[:,3],c="blue", marker='+', label='label2')
# 绘制簇的质心点
for i in range(length):
plt.annotate('center',xy=(center[i,2],center[i,3]),xytext=\
(center[i,2]+1,center[i,3]+1),arrowprops=dict(facecolor='yellow'))
plt.show()
2.1.可视化生成
代码如下(示例):
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
dataSet= iris.data[:, :4]
k = 3
centroids,clusterAssment = KMeans(dataSet,k)
draw(dataSet,centroids,clusterAssment)
3其他聚类算法进行鸢尾花分类
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn import datasets
# 直接从sklearn中获取数据集
iris = datasets.load_iris()
X = iris.data[:, :4] # 表示我们取特征空间中的4个维度
print(X.shape)
from sklearn.cluster import DBSCAN
# 导入数据集
iris = datasets.load_iris()
X = iris.data[:, :4] # 取前四个特征
# 使用DBSCAN聚类算法
dbscan = DBSCAN(eps=0.5, min_samples=5)
labels = dbscan.fit_predict(X)
# 绘制分类结果
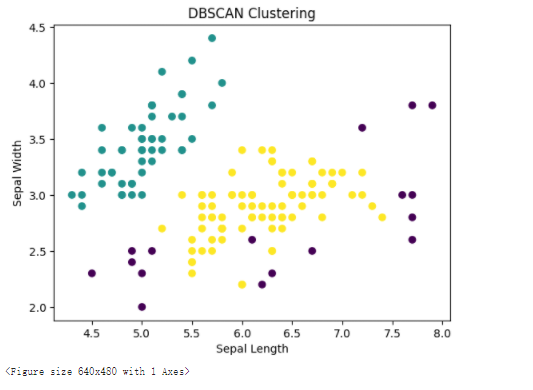
plt.scatter(X[:, 0], X[:, 1], c=labels)
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('DBSCAN Clustering')
plt.show()
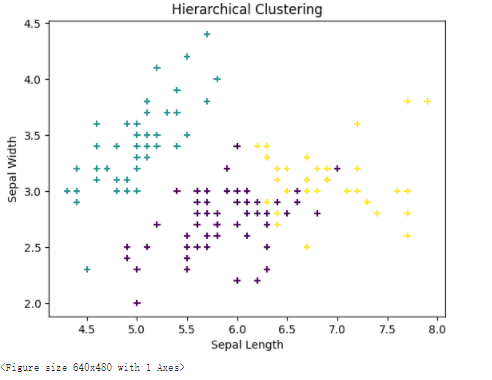
from sklearn.cluster import AgglomerativeClustering
# 使用层次聚类算法
hierarchical = AgglomerativeClustering(n_clusters=3)
labels = hierarchical.fit_predict(X)
# 绘制分类结果
plt.scatter(X[:, 0], X[:, 1], c=labels, marker='+')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('Hierarchical Clustering')
plt.show()