目录

概述       

一、固定旋转（Fix Angles）

二、欧拉旋转（Euler Angle）

 三、旋转矩阵小结

四、参考

---

概述       

 旋转矩阵是姿态的一种数学表达方式，或者笼统说变换矩阵是一种抽象的数学变量。其抽象在于当你看到数据，根本无法断定其正确性；往往只有转换为较为直观的欧拉角，然后大概目测估算（总不能拿着量角器去测量精度吧）。我们知道，姿态的数学形式有旋转矩阵（满足RTR=E）、欧拉角、旋转向量（角轴）、四元数（norm(x y z w) = 1）等。今天这里要讨论的是旋转矩阵相关理论基础。

       旋转矩阵常用于以下三种场景：

• 描述一个frame（坐标系）相对于另一个frame间的位姿；(如：描述相邻两帧间的相机运动)
• 描述一个point从一个frame变换到另一个frame；（其实点没动，只是在两个frame观测时，坐标不一样而已；如：；路标点点P在不同相机坐标系下坐标值不同，但在世界坐标系下是固定的）
• 描述一个point在同一个frame中的运动；（这里的点是运动了的，在VSLAM中应用较少）

 绕三个轴的旋转矩阵请按以下形式进行记忆，可能有些地方是下面的转置形式。

 （本博客和大多数论文资料一样，都是左乘原则）

一、固定旋转（Fix Angles）

       所谓固定旋转，就是按照物体外部固定轴旋转。这种旋转在工程中很常见，用的相对多一些（相对于下面的欧拉旋转），例如：旋转次序为X-Y-Z，那么旋转矩阵的形式为：RZRYRX。如下图，其实没什么好说。

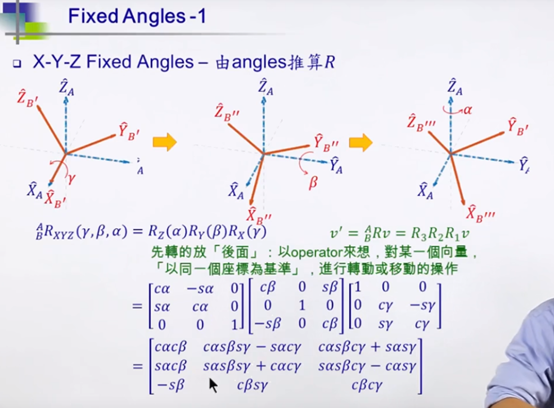
      已知旋转矩阵，怎么求解欧拉角呢？下图便是一种比较好的求解办法。我们知道，顺时针旋转180°和逆时针旋转180°是等效的（让机械臂旋转190°其实是走远路，因为旋转170°似乎更快），所以求解出来的欧拉角其取值范围最好是：[0°，180°] or [0°，-180°] 或者[-90°，90°]，这里采用的后者。下面代码中的atan2是matlab中的api，我们在这里简单验证下其与tan的区别：可以看到，当一个点在第三象限，如（-1， -1），在欧拉角中，其角度为：-135°，但是atan(-1/-1)算出来是45°，显然是错的。

>> atan(1) * 180 / pi

ans =

    45

>> atan2(1, 1) * 180 / pi

ans =

    45

>> atan2(-1, -1) * 180 / pi

ans =

  -135

>>

顺在在这里用Eigen验证下：（相关头文件（如Pose.h）去这个链接中查找： 基于Eigen的位姿转换-CSDN博客 ）不去下载，下面C++代码你都跑不了

#include"Pose.h"
#include<iostream>
using namespace std;

int main()
{
    Eigen::Matrix3d R1;
    R1 << 0.866, 0.433, 0.25, 0., 0.5, -0.866, -0.5, 0.75, 0.433;

    Pose pose1(R1);
    cout << "旋转矩阵 = " << endl; cout << pose1.rotation() << endl;
    cout << "欧拉角 = " << endl;   cout << pose1.euler_angle().transpose()*(180 / M_PI) << endl;
    cout << "四元数 = " << endl;   cout << pose1.quaternion().coeffs().transpose() << endl;
    cout << "角轴 = " << endl;
    cout << pose1.angle_axis().angle()* (180 / M_PI) << " " << pose1.angle_axis().axis().transpose() << endl;
    cout << "-----------------------------" << endl;
    return 1;
}

  打印结果：

旋转矩阵 =  0.866  0.433   0.25
            0    0.5 -0.866
            -0.5   0.75  0.433
欧拉角 =   63.4349  14.4779 -26.5651
四元数 =   0.482959  0.224145 -0.129407  0.836511
角轴 =     66.4519 0.881411 0.409071 -0.23617

可以看到Eigen的欧拉角结果和上述PPT中Matlab计算的结果不一样，但是他们旋转矩阵具体是一样的，这个是正常的，下面还会碰到。其实就是利用欧式旋转矩阵求解。欧拉角的解并不唯一，这个问题在手眼标定中验证过。 

二、欧拉旋转（Euler Angle）

        固定旋转与欧拉旋转的关系，例如：固定旋转次序为:XYZ，写成旋转矩阵则为：Rz*Ry*Rx；其等效的欧拉旋转次序为：ZYX，写成旋转矩阵则为：Rz*Ry*Rx，最后的映射矩阵是一样的，但是过程不一样，殊途同归。）例如下面例子：

ZYZ的欧拉旋转次序，这个我是实际“体验过”，那是在自研机械臂上示教器是数据。欧拉旋转的方式如下图：

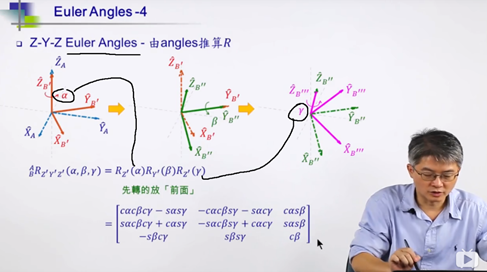
 形如固定旋转，我这里也给出：已经ZYZ类型欧拉旋转，求解欧拉角的一种方法：

针对上面等式：

这里用Eigen验证下， 对于等式左边：

1 #include"Pose.h"
 2 #include<iostream>
 3 using namespace std;
 4 
 5 int main()
 6 {
 7     // 低级错误：是60.0，不是60
 8     Eigen::Matrix3d R1;
 9     R1 = Eigen::AngleAxisd(60.0 / 180 * M_PI, Eigen::Vector3d::UnitX()) *
10          Eigen::AngleAxisd(30.0 / 180 * M_PI, Eigen::Vector3d::UnitY()) *
11           Eigen::AngleAxisd(              0.0, Eigen::Vector3d::UnitZ());
12 
13     Pose pose3(R1);
14     cout << "旋转矩阵 = " << endl; cout << pose3.rotation() << endl;
15     cout << "欧拉角 = " << endl;   cout << pose3.euler_angle().transpose()*(180 / M_PI) << endl;
16     cout << "四元数 = " << endl;   cout << pose3.quaternion().coeffs().transpose() << endl;
17     cout << "角轴 = " << endl;
18     cout << pose3.angle_axis().angle()* (180 / M_PI) << " " << pose3.angle_axis().axis().transpose() << endl;
19     cout << "-----------------------------" << endl;
22     return 1;
23 }

针对等式右边，同理有：

#include"Pose.h"
#include<iostream>
using namespace std;

int main()
{
    Eigen::Vector3d RPY;
    RPY << -56.3 / 180 * M_PI, 64.3 / 180 * M_PI, 73.9 / 180 * M_PI;

    cout << RPY(2, 0) << endl;


    Eigen::Matrix3d R2;
    // note: ZYZ
    R2 = Eigen::AngleAxisd(RPY(0, 0), Eigen::Vector3d::UnitZ()) *
         Eigen::AngleAxisd(RPY(1, 0), Eigen::Vector3d::UnitY()) *
         Eigen::AngleAxisd(RPY(2, 0), Eigen::Vector3d::UnitZ());
    Pose pose4(R2);
    cout << "旋转矩阵 = " << endl; cout << pose4.rotation() << endl;
    cout << "欧拉角 = " << endl;   cout << pose4.euler_angle().transpose()*(180 / M_PI) << endl;
    cout << "四元数 = " << endl;   cout << pose4.quaternion().coeffs().transpose() << endl;
    cout << "角轴 = " << endl;
    cout << pose4.angle_axis().angle()* (180 / M_PI) << " " << pose4.angle_axis().axis().transpose() << endl;
    cout << "-----------------------------" << endl;

    return 1;
}

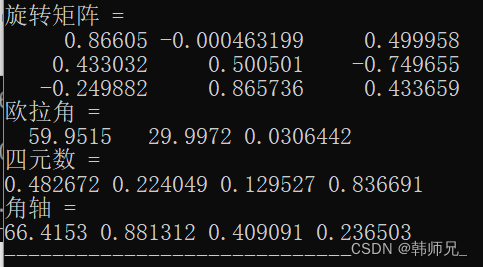
对比两种旋转方式，可以看到Eigen计算的结果完全一致；但是比较有意思的是，对于下面，我用的欧拉角明明是( -56.3, 64.3, 73.9 )（ZYZ），结果打印输出的。欧拉角居然是(59.9, 29.99, 0.031)。这是由于我写的Pose类底层，我只定义了ZYX的固定旋转方式。同时，也说明了，同一个旋转矩阵，可能对应不同的旋转方式(如：欧拉旋转、固定旋转)，不同的旋转欧拉角、甚至不同的旋转次序

 三、旋转矩阵小结

       欧拉旋转和固定旋转的次序有效的排列组合为：12 = 3 * 2 * 2

       姿态的数学形式有旋转矩阵（约束：RTR=E）、欧拉角（万向锁问题）、旋转向量（角轴）、四元数（约束norm(x y z w) = 1），所以VSLAM在对位姿进行优化的时候，

为了避免“带约束的优化”问题，一般都会采用旋转向量的形式作为姿态。

四、参考

（台大机器人学之运动学——林沛群）