引入
二叉查找树
二叉查找树(Binary Search Tree),又名二叉搜索树。满足以下性质:
- 对于非空的左子树,左子树点权值小于根节点。
- 对于非空的右子树,左子树点权值大于根节点。
- 二叉查找树的左右子树均是二叉查找树。
平衡树
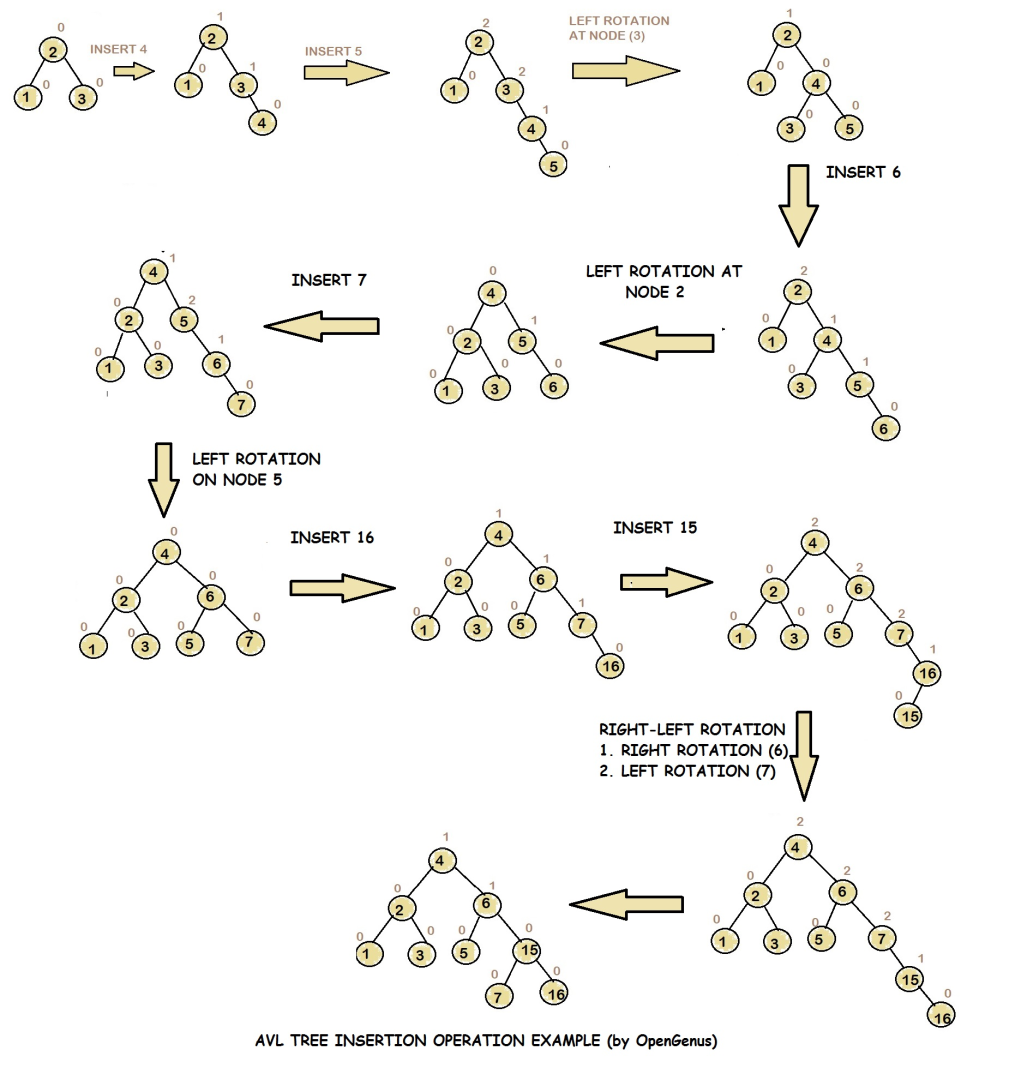
在维持二叉查找树性质的基础上,通过改变其形态,控制深度在 log n \log n logn 级别。
平衡树左右两个子树高度差不大于 1 1 1,否则需要进行左旋 / 右旋操作。
pb_ds
在 C++ 的 pb_ds 中有封装好的平衡树。
tree 类型的平衡树常数稍大,速度略慢。
声明方式
有以下声明(来源于官方文档):
template<
typename Key,
typename Mapped,
typename Cmp_Fn = std::less<Key>,
typename Tag = rb_tree_tag,
template<
typename Const_Node_Iterator,
typename Node_Iterator,
typename Cmp_Fn_,
typename Allocator_>
class Node_Update = null_tree_node_update,
typename Allocator = std::allocator<char> >
class tree;
常用的定义方式为 tree<int,null_type,less<int>,rb_tree_tag,tree_order_statistics_node_update>。
- 第一个参数表示存储元素(Key)的类型;
- 第二个参数表示映射规则(Mapped-Policy)的类型,常用的是
null_type,表示无映射; - 第三个参数表示比较规则(
Cmp_Fn); - 第四个参数表示平衡树的类型(
Tag),有rb_tree_tag(红黑树)、splay_tree_tag等; - 第五个参数表示更新节点的策略(
Node_Update),默认为null_node_update,如果要使用查询排名相关操作,需要使用tree_order_statisitics_node_update。
常用操作
其中 x 表示存储元素的类型。
insert(x):插入元素 x x x。erase(x):删除元素 x x x。order_of_key(x):查询元素 x x x 的排名(前面有多少数比 x x x 小),返回值为整数。find_by_order(x):查询排名为 x x x 的元素对应的迭代器。lower_bound(x)、upper_bound(x):返回迭代器。join(x):将 x x x 树并入当前树,要求两树值域不能重叠。合并后 x x x 树被清空。split(x,b):小于等于 x x x 的属于当前树,其余的属于 b b b 树。size():返回大小。
以下是 P3369 【模板】普通平衡树 的代码。
注意用 pb_ds 实现的 tree 类似于一个 set,元素是不可重的。所以我们把元素以 pair 的形式存储,再记录一个元素被插入到 tree 的时间。
prev(it) 函数可以求迭代器 it 的前驱(即前一个位置)。注意求
x
x
x 的后继时,用 upper_bound() 操作的键值对应该是 pair<x,INT_MAX>,避免查找到和
x
x
x 相等但插入时间比
x
x
x 晚的元素。
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;
using namespace std;
tree<pair<int,int>,null_type,less<pair<int,int> >,rb_tree_tag,tree_order_statistics_node_update> t;
int main()
{
int n;cin>>n;
for(int i=1;i<=n;i++)
{
int op,x;cin>>op>>x;
if(op==1) t.insert({x,i});
if(op==2) t.erase(t.upper_bound({x,0}));
if(op==3) cout<<t.order_of_key({x,0})+1<<endl;
if(op==4)
{
auto it=t.find_by_order(x-1);
cout<<(*it).first<<endl;
}
if(op==5)
{
auto it=prev(t.lower_bound({x,0}));
cout<<(*it).first<<endl;
}
if(op==6)
{
auto it=t.upper_bound({x,INT_MAX});
cout<<(*it).first<<endl;
}
}
return 0;
}