Markov Chain Fingerprinting to Classify Encrypted Traffic 论文笔记

news2024/11/23 21:17:41

0.Abstract
在本文中，提出了用于SSL/TLS会话中传输的应用程序流量的随机指纹。这个指纹基于一阶齐次马尔可夫链，模型识别应用程序的准确率，并提供了检测异常对话的可能性。
1.Introduction
通过SSL/TLS会话时的头部信息创建统计指纹，用于分类应用流量。研究了 12 个使用 SSL/TLS 的代表性应用程序的马尔可夫链指纹，建立的模型展现出特定的结构，这种结构能够通过比较应用程序流量和和它带有指纹的消息序列对加密的应用程序流量分类。
2.SSL/TLS Overview
在 SSL/TLS 握手期间，很多信息都作为明文发送。但是，在服务器 Hello Done 或 Change Cipher SpecProtocol 消息之后，只有协议类型、记录的长度和 SSL/TLS 版本没有被加密。
在这里插入图片描述

SSL/TLS协议交流流程
在这里插入图片描述

将协议中的消息类别用数字表示，用于建图和分析。
主要分析服务端，文章认为客户端有个性差异，但是服务端没有。

III. MARKOV CHAIN FINGERPRINTS
Xt表示t时刻的状态，it∈{1,2,3…s}，it表示一个SSL/TLS信息类别或者在一次TCP片段中传输的一系列SSL/TLS信息类别。
假设满足一阶马尔科夫链：
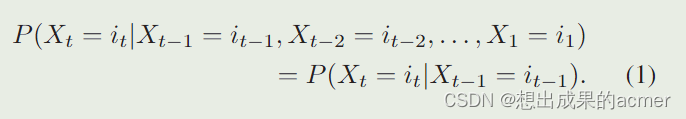
在这里插入图片描述

进一步假设满足齐次性：
在这里插入图片描述

设置Q和W是进入session和离开session的概率分布。
注意Q和W是独立于马尔科夫链的，他们只是提供了进入马尔科夫链和离开马尔科夫链的概率。
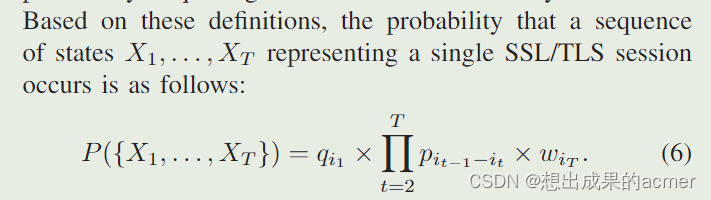
在这里插入图片描述

基于以上定义，某个长度为T的序列，他是SSL/TLS session的概率就如公式（6）所示。因为序列是X1、X2…XT这些消息，所以计算概率肯定是第一个消息是X1进入的概率，然后按照给定的消息序列走的概率，对应连乘，最后乘一个离开的概率。（为什么最后乘一个离开的概率？）

交叉验证:
4折交叉验证。
四个数据集，每次都是一个数据集训练，三个数据集测试。（为什么和常规理解是反着的）
在这里插入图片描述

验证相当于是一个多假设决策问题。
最大似然估计，把所有应用(12个应用)中消息序列的概率P最大的当作该消息序列的对应应用。因为最大似然估计认为模型求出的消息序列概率P就是他属于某个应用的可能性。最大似然估计的核心:存在即合理。
为了让实验结果更有说服力，在第一次实验之后在一年半的时间内又做了两次实验，观察之前得到的马尔科夫链指纹是否仍然有效。总而言之，应用程序指纹可能会随着时间的推移而演变，并且需要定期甚至恒定的更新。

V. DISCUSSION
讨论本文的方法能够精确区分应用程序的原因:
1.许多协议并不完全遵守RFC规范，且行为与普通的SSL/TLS协议具有细微的差异。这样产生了高度分化的应用，与之对应方便求出高度分化的马尔科夫链指纹，进而进行应用的分类。
2.SSL/TLS隧道使用频率正在逐渐增加，而使用SSL/TLS加强安全性的不多，比如Skype用自己的安全性和实时性通信协议，仅使用SSL/TLS隧道来绕过防火墙。因此，SSL/TLS 堆栈指纹被简化为几个转换，这与其他模型有很大不同。
3.一些 SSL/TLS 协议消息被定义为可选的或上下文相关的。例如，在我们研究的前两个数据集中，我们没有观察到 PayPal 和 Twitter 会话中的任何服务器密钥交换消息，而在 Dropbox 的情况下，它总是遵循证书消息。这样，应用之间的差异就容易找到。
4.应用实现的功能不同。Twitter只有少数会话转换，用户能够发送很多基于文本的消息。Gadu-Gadu 协议的情况下，我们可以观察到一百多个会话。

VII. CONCLUSIONS
通过一阶马尔可夫链建立的分类模型，达到了不错的分类效果。

优点:
1.分类效果较好
2.方法简单，方法需要的时间、资源要求低，代码实现简单。
缺点:
1.假设满足马尔可夫链，其实研究问题不完全满足马尔可夫链的性质。
2.每个状态基于单个变量（消息类型），状态表达能力有限，容易导致指纹的低区分度。
解决方案:
文章使用1阶马尔可夫链，如果尝试用n阶马尔可夫链，可能与实际问题关联更加紧密。有助于解决缺点1
每个状态采用<消息类别，分组长度>二元组来表征，可能能表达更好的状态，有助于解决缺点2

写了一份简单的马尔可夫链python代码，输入n，输入表示初始状态的概率分布（n维行向量）与状态转移矩阵（n*n的矩阵），可以判断迭代一定次数后是否达到稳态。

import numpy as np

res = []
def check(a,b): #判断相邻两个状态的Π是否相等
    tmp = a - b
    # print(tmp)
    if all(abs(i)<=1e-10 for i in tmp) > 0:
        return True
    return False
def markov(pai,A): #马尔可夫链，给定初始状态和状态转移矩阵，求之后的每个状态。如果达到稳态，返回True
    res.append(pai)
    for i in range(1,10000):
        tmp = np.dot(res[i-1],A)
        res.append(tmp)
        if check(res[i-1],res[i]):
            return True
    return False
def main():
    n = int(input())
    pai = list(map(float,input().split()))
    A = []
    for _ in range(n):
        tmp = list(map(float,input().split()))
        A.append(tmp)
    print("初始状态:",end="")
    print(pai)
    if markov(pai,A):
        print("稳态:", end="")
        print(res[-1])
if __name__=='__main__':
    main()
    main()
'''
3
0.2 0.3 0.5
0.2 0.6 0.2
0.3 0 0.7
0.5 0 0.5

3
0.7 0.2 0.1
0.2 0.6 0.2
0.3 0 0.7
0.5 0 0.5
'''